初中数学人教版九下27.2.3相似三角形应用举例第2课时 教案
文档属性
| 名称 | 初中数学人教版九下27.2.3相似三角形应用举例第2课时 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 222.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 19:35:11 | ||
图片预览


文档简介
27.2.3相似三角形应用举例
(第2课时)
一、教学内容分析
本节课是相似三角形应用举例第二课时,是对建立数学模型,利用相似三角形性质解决实际问题进一步巩固.视线遮挡问题更具挑战性,题目中没有直接给出相似三角形,需要学生分析在不同的行进位置时观察大树CD的不同情况,自己构造相似模型解决实际问题.通过本课知识的学习,将进一步训练学生的应用意识,加深学生对于相似三角形的理解和认识.
二、教学目标
1. 通过本节对视线遮挡问题的研究,学生能综合运用相似三角形的判定方法和性质解决不能直接测量的物体的高度和长度问题
2. 经历“实际问题——建立模型——拓展应用”的过程,提高学生将实际问题转化为数学问题的方法,体会转化思想、建模思想在解决实际问题中的应用.
三、教学重难点
【重点】运用相似三角形有关知识,解决不能直接测量的物体的长度和高度等一些实际问题.
【难点】从实现遮挡问题中抽象出相似模型.
四、教学方法
启发式教学与探究式教学相结合来展开分解难点、突出重点.始终体现以学生自主学习及合作交流为主的新课程理念,从学生的经验、生活实际出发,创设情景,引导学生去发现、分析、解决问题.
五、教学过程
(一)创设情境 导入新课
1.运用相似三角形有关知识测量物高的基本模型有哪些?
2. 如图所示,利用标杆测量旗杆高度时,此方案必须满足什么条件?(教师动画演示小红行进过程)
追问:如果小红行进到什么位置只能看到旗杆的顶端?
【答案或提示】
1.
2.保证眼睛、标杆顶端、旗杆顶端,三点共线.
行进到眼睛、标杆顶端、旗杆顶端,三点共线时.
设计意图:以问题作为知识链条,引导学生温故知新,尤其动画演示,使学生形象感知题目中“三点共线”的重要意义,并分解了课教学的难点.
(二)精讲例题 强化重点
例题:如图,左、右并排的两棵大树的高分别为AB=8 m和CD=12 m,两树底部的距离BD=5m,一个人估计自己眼睛距地面1.6 m .她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端点C了?
1.此人行进到什么位置只能看到右边较高的树的顶端点C了?
2.构建相似模型,将实际问题转化为数学问题.
3.梳理解题思路并完成解题过程.
4.试着归纳一下用相似三角形解决实际问题时的一般步骤.
【答案或提示】
1. 此人行进到眼睛F与两棵树顶端点A.C共线时,只能看到右边较高的树的顶端点C.
2.
3.解:如图所示,当E.A.C在一条直线上时
∵⊥l,CD⊥l
∴AB∥CD,
∴△AEH∽△CEK
∴,
即
解得 EH=8
由此可知,如果观察者继续前行,当她与左边的树距离小于8m时,由于这棵树的遮挡,她看不到右边树的顶端C.
4. 一般步骤:图中找相似,相似得比例,比例来计算,计算求线段.
设计意图:由测量旗杆问题直接过渡到例题,题目设计衔接紧凑,学生拾阶而上,找到解决问题的关键点,构造相似三角形从而解决问题,突破教学重难点.
(三)当堂检测 巩固新知
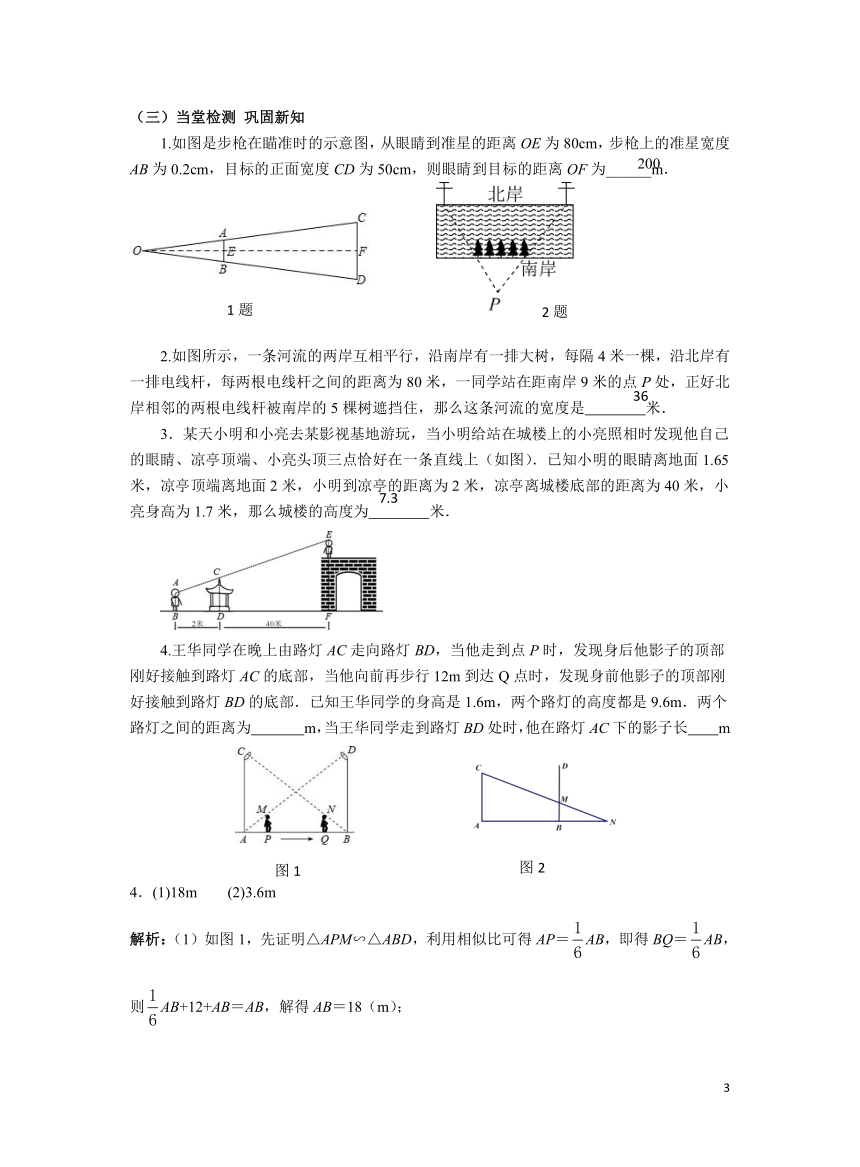
1.如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF为______m.
2.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 米.
3.某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高为1.7米,那么城楼的高度为 米.
4.王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.两个路灯之间的距离为 m,当王华同学走到路灯BD处时,他在路灯AC下的影子长 m
4.(1)18m (2)3.6m
解析:(1)如图1,先证明△APM∽△ABD,利用相似比可得AP=AB,即得BQ=AB,则AB+12+AB=AB,解得AB=18(m);
(2)如图2,他在路灯AC下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得,然后利用比例性质求出BN即可.
设计意图:巩固新知.
(四)课堂小结
这节课我们学到了什么?
1.如何解决不能直接测量的物体的长度和高度的实际问题?
2.学习过程中体现了怎样的数学思想?
设计意图:对所学知识进行梳理,并对知识进一步内化,系统化.
(五)作业布置
A组: 1.为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E.C.A三点共线,则旗杆AB的高度为( A )
A.13.5米 B.12.5米 C.11.9米 D.10.5米
【解析】利用三角形相似中的比例关系,首先由题目和图形可看出,求AB的长度分成了2个部分,AH和HB部分,其中HB=EF=1.6m,剩下的问题就是求AH的长度,利用△CGE∽△AHE,即可求得AH,最后根据AB=AH+HB即可解题.
【详解】设CD与EH交于点G
由题意得:EF=GD=BH=1.6,BD=EH=15,EG=DF=2
∴CG=CD-GD=1.4,
∵CD⊥FB,AB⊥FB,
∴CD∥AB,
∴△CGE∽△AHE,
∴,
即:,
∴AH=11.9,
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
2.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
【解析】从A点走到B点,身影的长度是变短了3.5m.根据题意可得OB=6m,根据平行得△DBN∽△PON,△MAC∽△MOP列出比例式,代入数据计算即可
B组:1.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,出南门 步恰好看到位于A处的树木(即点D在直线AC上).
【解析】本题只需要证出△CDK∽△DAH,利用相似三角形的性质可以得到:,然后可以求出CK的值,得出答案.
【详解】
解:由题意可知: DE=DG=200,AH=15
∵H为GD的中点,K为DE的中点
DH=100,DK=100
∵AH∥DK
∴∠CDK=∠A
而∠CKD=∠AHD
∴△CDK∽△DAH
∴
即,
∴CK=
2. 某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=1.2米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.8米, CG=20米,请你根据以上数据,估算古塔的高度AB.
【解析】68.7米
根据题意可得△CDE∽△ABE∽△FAB,从而得到,进而得到 ,解得AC=40米,从而得到,即可求解.
【详解】
解:根据题意得:AB⊥AF,CD⊥AF,HG⊥AF,GH=CD
∴HG∥AB,CD∥AB
∴△CDE∽△ABE,△FGH∽△FAB ,
∴,
∵,
∵米,米,CG=20米,
∴ ,解得:AC=40 米,
∴ ,解得:AB=68.7 米,
答:古塔的高度约为68.7米.
设计意图:布置分层作业,照顾不同学情的学生,进行自我检测
六、板书设计
27.2.3相似三角形应用举例
(第2课时)
1.相似三角形解决时间问题基本模型.
2.例题:
3. 相似三角形解决实际问题时的一般步骤:图中找相似,相似得比例,比例来计算,计算求线段.
1
(第2课时)
一、教学内容分析
本节课是相似三角形应用举例第二课时,是对建立数学模型,利用相似三角形性质解决实际问题进一步巩固.视线遮挡问题更具挑战性,题目中没有直接给出相似三角形,需要学生分析在不同的行进位置时观察大树CD的不同情况,自己构造相似模型解决实际问题.通过本课知识的学习,将进一步训练学生的应用意识,加深学生对于相似三角形的理解和认识.
二、教学目标
1. 通过本节对视线遮挡问题的研究,学生能综合运用相似三角形的判定方法和性质解决不能直接测量的物体的高度和长度问题
2. 经历“实际问题——建立模型——拓展应用”的过程,提高学生将实际问题转化为数学问题的方法,体会转化思想、建模思想在解决实际问题中的应用.
三、教学重难点
【重点】运用相似三角形有关知识,解决不能直接测量的物体的长度和高度等一些实际问题.
【难点】从实现遮挡问题中抽象出相似模型.
四、教学方法
启发式教学与探究式教学相结合来展开分解难点、突出重点.始终体现以学生自主学习及合作交流为主的新课程理念,从学生的经验、生活实际出发,创设情景,引导学生去发现、分析、解决问题.
五、教学过程
(一)创设情境 导入新课
1.运用相似三角形有关知识测量物高的基本模型有哪些?
2. 如图所示,利用标杆测量旗杆高度时,此方案必须满足什么条件?(教师动画演示小红行进过程)
追问:如果小红行进到什么位置只能看到旗杆的顶端?
【答案或提示】
1.
2.保证眼睛、标杆顶端、旗杆顶端,三点共线.
行进到眼睛、标杆顶端、旗杆顶端,三点共线时.
设计意图:以问题作为知识链条,引导学生温故知新,尤其动画演示,使学生形象感知题目中“三点共线”的重要意义,并分解了课教学的难点.
(二)精讲例题 强化重点
例题:如图,左、右并排的两棵大树的高分别为AB=8 m和CD=12 m,两树底部的距离BD=5m,一个人估计自己眼睛距地面1.6 m .她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端点C了?
1.此人行进到什么位置只能看到右边较高的树的顶端点C了?
2.构建相似模型,将实际问题转化为数学问题.
3.梳理解题思路并完成解题过程.
4.试着归纳一下用相似三角形解决实际问题时的一般步骤.
【答案或提示】
1. 此人行进到眼睛F与两棵树顶端点A.C共线时,只能看到右边较高的树的顶端点C.
2.
3.解:如图所示,当E.A.C在一条直线上时
∵⊥l,CD⊥l
∴AB∥CD,
∴△AEH∽△CEK
∴,
即
解得 EH=8
由此可知,如果观察者继续前行,当她与左边的树距离小于8m时,由于这棵树的遮挡,她看不到右边树的顶端C.
4. 一般步骤:图中找相似,相似得比例,比例来计算,计算求线段.
设计意图:由测量旗杆问题直接过渡到例题,题目设计衔接紧凑,学生拾阶而上,找到解决问题的关键点,构造相似三角形从而解决问题,突破教学重难点.
(三)当堂检测 巩固新知
1.如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF为______m.
2.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 米.
3.某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高为1.7米,那么城楼的高度为 米.
4.王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.两个路灯之间的距离为 m,当王华同学走到路灯BD处时,他在路灯AC下的影子长 m
4.(1)18m (2)3.6m
解析:(1)如图1,先证明△APM∽△ABD,利用相似比可得AP=AB,即得BQ=AB,则AB+12+AB=AB,解得AB=18(m);
(2)如图2,他在路灯AC下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得,然后利用比例性质求出BN即可.
设计意图:巩固新知.
(四)课堂小结
这节课我们学到了什么?
1.如何解决不能直接测量的物体的长度和高度的实际问题?
2.学习过程中体现了怎样的数学思想?
设计意图:对所学知识进行梳理,并对知识进一步内化,系统化.
(五)作业布置
A组: 1.为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E.C.A三点共线,则旗杆AB的高度为( A )
A.13.5米 B.12.5米 C.11.9米 D.10.5米
【解析】利用三角形相似中的比例关系,首先由题目和图形可看出,求AB的长度分成了2个部分,AH和HB部分,其中HB=EF=1.6m,剩下的问题就是求AH的长度,利用△CGE∽△AHE,即可求得AH,最后根据AB=AH+HB即可解题.
【详解】设CD与EH交于点G
由题意得:EF=GD=BH=1.6,BD=EH=15,EG=DF=2
∴CG=CD-GD=1.4,
∵CD⊥FB,AB⊥FB,
∴CD∥AB,
∴△CGE∽△AHE,
∴,
即:,
∴AH=11.9,
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
2.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
【解析】从A点走到B点,身影的长度是变短了3.5m.根据题意可得OB=6m,根据平行得△DBN∽△PON,△MAC∽△MOP列出比例式,代入数据计算即可
B组:1.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,出南门 步恰好看到位于A处的树木(即点D在直线AC上).
【解析】本题只需要证出△CDK∽△DAH,利用相似三角形的性质可以得到:,然后可以求出CK的值,得出答案.
【详解】
解:由题意可知: DE=DG=200,AH=15
∵H为GD的中点,K为DE的中点
DH=100,DK=100
∵AH∥DK
∴∠CDK=∠A
而∠CKD=∠AHD
∴△CDK∽△DAH
∴
即,
∴CK=
2. 某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=1.2米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.8米, CG=20米,请你根据以上数据,估算古塔的高度AB.
【解析】68.7米
根据题意可得△CDE∽△ABE∽△FAB,从而得到,进而得到 ,解得AC=40米,从而得到,即可求解.
【详解】
解:根据题意得:AB⊥AF,CD⊥AF,HG⊥AF,GH=CD
∴HG∥AB,CD∥AB
∴△CDE∽△ABE,△FGH∽△FAB ,
∴,
∵,
∵米,米,CG=20米,
∴ ,解得:AC=40 米,
∴ ,解得:AB=68.7 米,
答:古塔的高度约为68.7米.
设计意图:布置分层作业,照顾不同学情的学生,进行自我检测
六、板书设计
27.2.3相似三角形应用举例
(第2课时)
1.相似三角形解决时间问题基本模型.
2.例题:
3. 相似三角形解决实际问题时的一般步骤:图中找相似,相似得比例,比例来计算,计算求线段.
1
