初中数学人教版八下19.2.3一次函数与方程、不等式教案
文档属性
| 名称 | 初中数学人教版八下19.2.3一次函数与方程、不等式教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 485.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 20:04:39 | ||
图片预览

文档简介
19.2.3一次函数与方程、不等式
教学内容分析
函数、方程和不等式是初中数学的核心内容,函数是联系方程、不等式的纽带.通过函数图象,可以直观地表示方程(组)和不等式的解或解集的含义,用函数的观点看一元一次方程,则可以把解一元一次方程理解为已知一次函数的函数值求对应的自变量的值;用函数的观点看二元一次方程,则以二元一次方程的解为坐标的点集就是一次函数的图象,二元一次方程组的解就是相应的两个一次函数图象(两条直线)的交点坐标,用函数的观点看一元一次不等式,它的解集就是使得函数值在某个范围的自变量的取值范围,研究函数、方程、不等式之间的联系可以深化相关知识的优化知识结构.建立这种联系的关键是建立一次函数与二元一次方程的联系.
教学目标
1.认识一次函数与一元一次方程,二元一次方程(组),一元一次不等式之间的联系,会用数点解方程和不等式及其解成解集的意义;
2.经历用函数图象表示方程和不等式的过程,进一步体会“以形表数,以数释形”的数形结合思想;
教学重难点
【重点】理解一次函数与二元一次方程(组)的联系.
【难点】把一次函数图象上点的坐标与方程(组)的解建立联系.
教学方法
问题启发法、观察归纳法、探究法.
教学过程
(一)情境导入
今天数学王国搞了个家庭Party,各个成员按照自己所在的集合就坐,这时来了“x+y=5”.
如果是你,你会让它坐在哪儿?
意图:设置数学分类的有趣情境,让学生思考一次函数和二元一次方程之间的区别和联系,从而引入课题.
效果:引发了学生对一次函数和方程间区别与联系的思考.
新课讲授
一次函数与一元一次方程
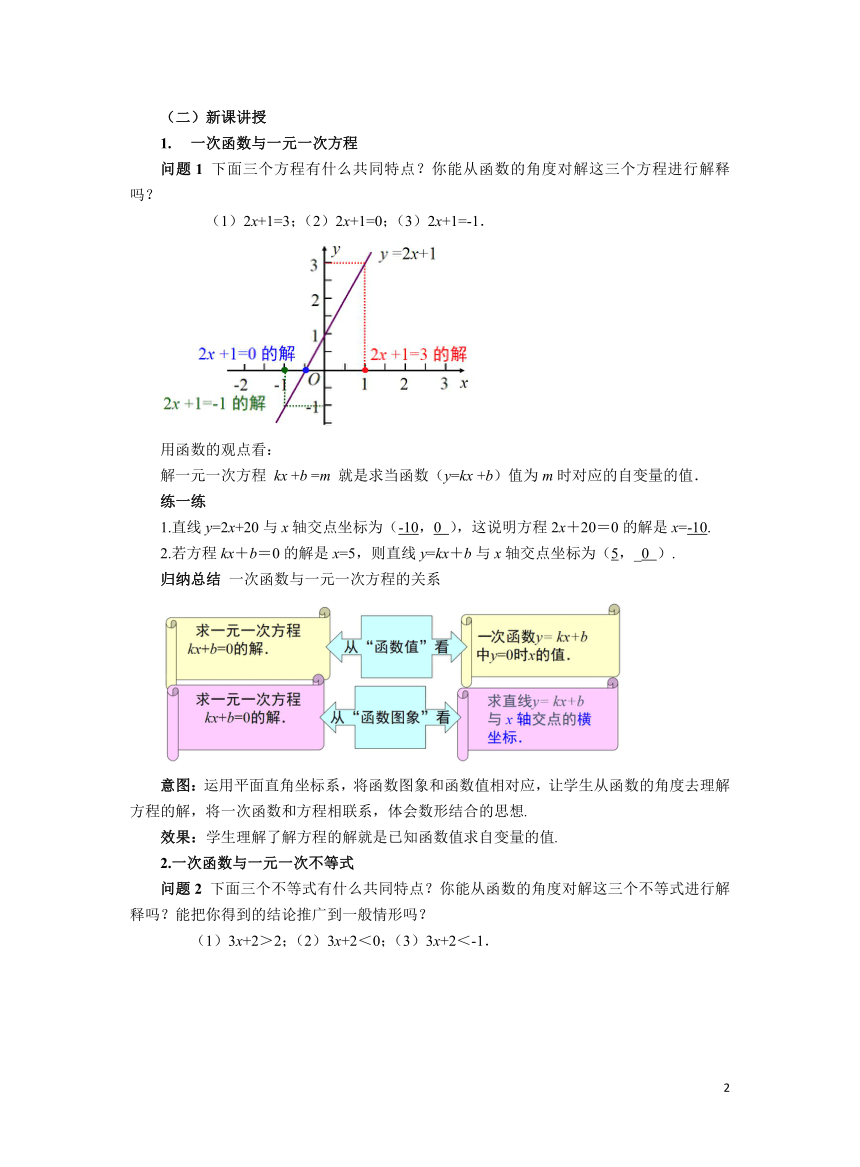
问题1 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程 kx +b =m 就是求当函数(y=kx +b)值为m时对应的自变量的值.
练一练
1.直线y=2x+20与x轴交点坐标为(-10,0 ),这说明方程2x+20=0的解是x=-10.
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(5,_0 ).
归纳总结 一次函数与一元一次方程的关系
意图:运用平面直角坐标系,将函数图象和函数值相对应,让学生从函数的角度去理解方程的解,将一次函数和方程相联系,体会数形结合的思想.
效果:学生理解了解方程的解就是已知函数值求自变量的值.
2.一次函数与一元一次不等式
问题2 下面三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b的函数值小于c的对应的自变量取值范围.
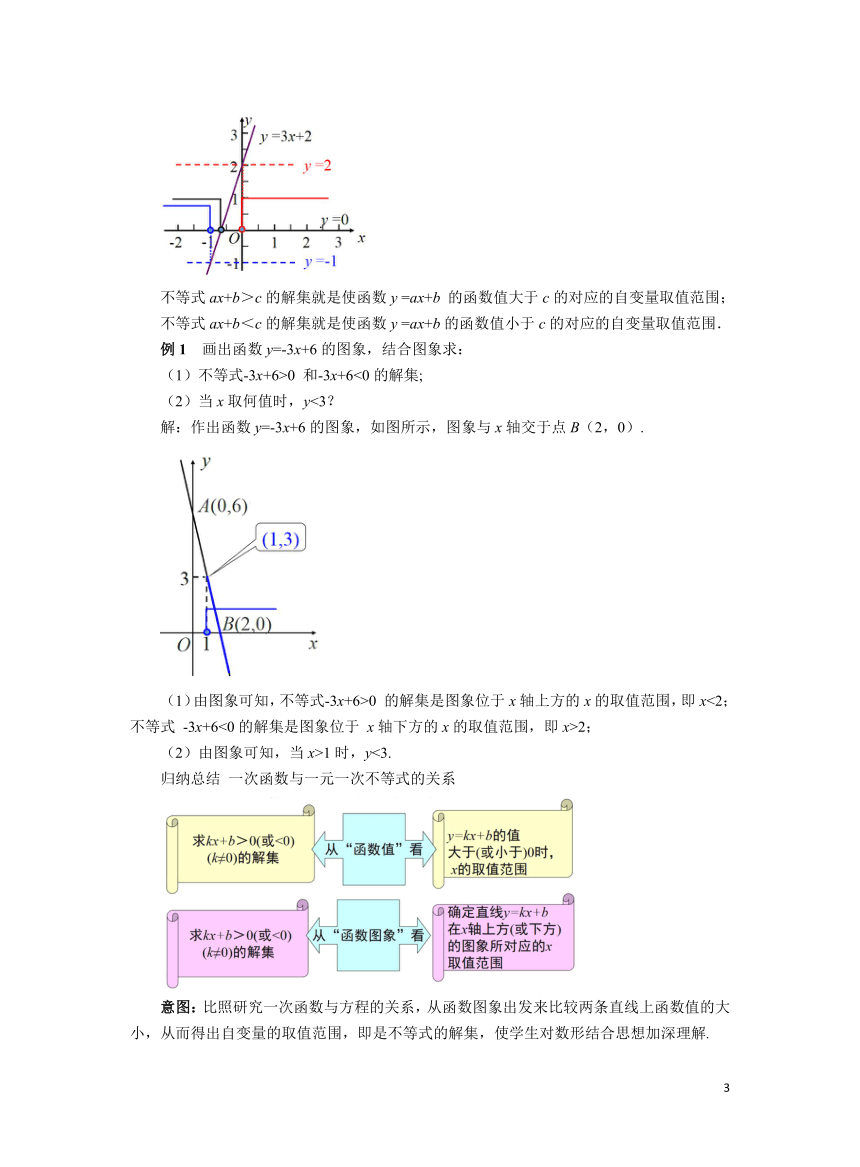
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
(2)由图象可知,当x>1时,y<3.
归纳总结 一次函数与一元一次不等式的关系
意图:比照研究一次函数与方程的关系,从函数图象出发来比较两条直线上函数值的大小,从而得出自变量的取值范围,即是不等式的解集,使学生对数形结合思想加深理解.
效果:学生明白了一次函数与一元一次不等式的关系,学会了如何从函数图象上求一元一次不等式的解集.
3.一次函数与二元一次方程组
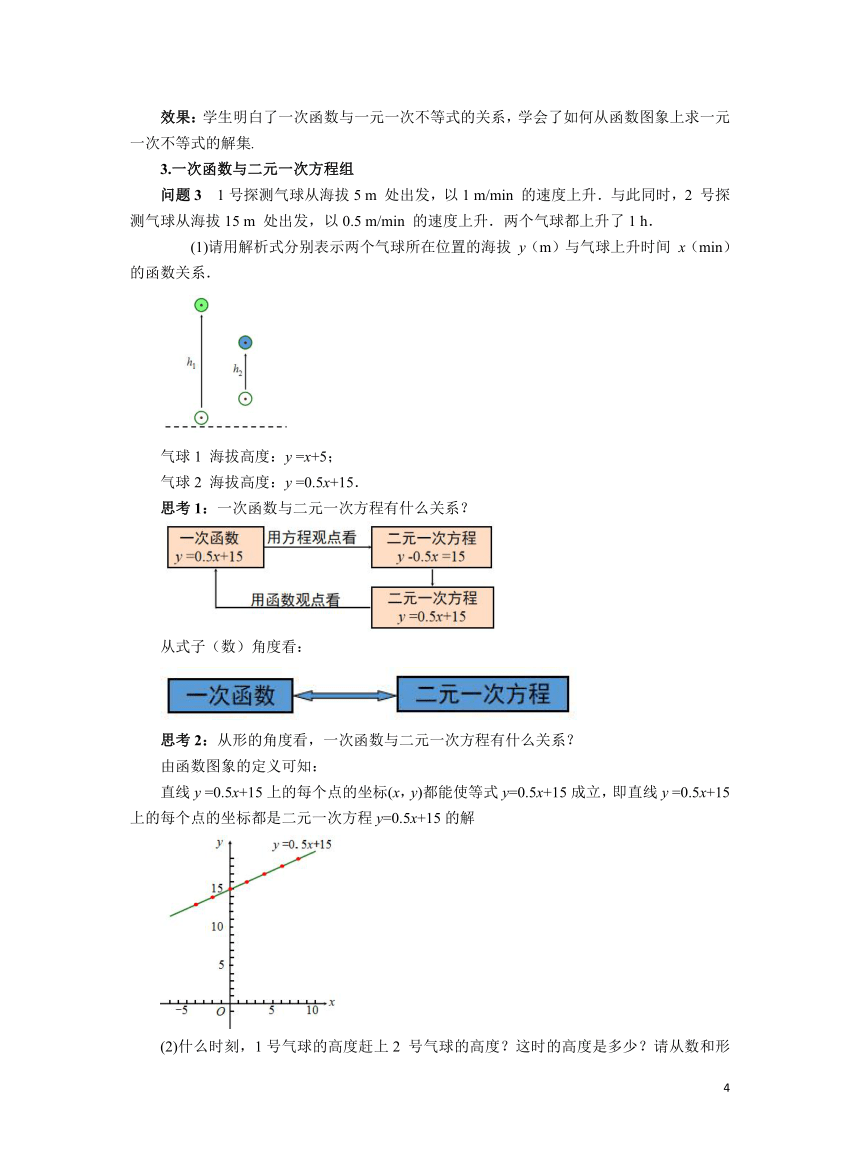
问题3 1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气球所在位置的海拔 y(m)与气球上升时间 x(min)的函数关系.
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
思考1:一次函数与二元一次方程有什么关系?
从式子(数)角度看:
思考2:从形的角度看,一次函数与二元一次方程有什么关系?
由函数图象的定义可知:
直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解
(2)什么时刻,1号气球的高度赶上2 号气球的高度?这时的高度是多少?请从数和形两方面分别加以研究.
从数的角度看:
解方程组
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
从形的角度看,二元一次方程组与一次函数有什么关系?
二元一次方程组的解就是相应的两个一次函数图象的交点坐标.
归纳总结 一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
意图:让学生用方程观点看一次函数,发现一次函数的表达式是一个二元一次方程.引导学生用函数的观点,从数和形两方面深化对二元一次方程组解的认识.通过式子之间的转换,让学生体会只要把未知数和变量的角色互换,则二元一次方程与一次函数也实现了互相转化.
效果:学生理解了一次函数与二元一次方程(组)间的联系,再次体会了数形结合思想.
观察函数图象,直接回答下列问题:
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
解:(1)20min后,1 号气球比2 号气球高.
(2)0~20min时,1 号气球比2 号气球高.
例2 如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求直线l1与l2的解析式,进而通过方程组求出交点坐标.
解:因为直线l1过点(-1,0),(0,2) ,用待定系数法可求得直线l1的解析式为y =2x+2.同理可求得直线l2的解析式为y =-x+3.
解方程组得
即直线l1与l2的交点坐标为
练一练 如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组的解是多少?
解:此方程组的解是
课堂练习
1.一次函数y=kx+3的图象如图所示,则方程kx+3=0的解为x=-3.
若方程组的解为,则一次函数y=2x+1与y=3x-1的图象交点坐标为(2,5).
小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1.l2如图 ,他解的这个方程组是( D )
4.一次函数y1=4x+5与y2=3x+10的图象如图所示,则4x+5>3x+10的解集是( B )
A.x<5
B.x>5
C.x>-5
D.x>25
意图:加深对一次函数与方程(组)、不等式的理解,巩固数形结合思想.
效果:检测了学生对本节课知识的掌握和运用情况.
(四)课堂小结
教师引导学生回顾本节课所学的主要内容,通过相互交流分享观点:
1. 一次函数与一元一次方程:
对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
2.一次函数与一元一次不等式:
对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
3.一次函数与二元一次方程组:
求对应两条直线交点的坐标 .
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能,培养提升数学素养.
效果:学生对本节课所学知识有了系统的回顾.
(五)作业布置
完成配套练习
板书设计
19.2.3一次函数与方程、不等式
1. 一次函数与一元一次方程:
对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
2.一次函数与一元一次不等式:
对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
3.一次函数与二元一次方程组:
求对应两条直线交点的坐标 .
教学反思
学生已经分别学习过一次函数、一元一次方程,二元一次方程组和一元一次不等式,知道它们都是刻画现实问题中数量关系的重要模型,但没有建立这些知识之间的有效联系.本节课重点是在平面直角坐标系中,利用函数图象从“数”和“形”两个方面来理解一次函数与一元一次方程、一元一次不等式、二元一次方程组之间的联系,体会从数量分析上他们是本质一样的,只是分析的角度是函数或方程的不同,从而培养学生数形结合的思想.
1
教学内容分析
函数、方程和不等式是初中数学的核心内容,函数是联系方程、不等式的纽带.通过函数图象,可以直观地表示方程(组)和不等式的解或解集的含义,用函数的观点看一元一次方程,则可以把解一元一次方程理解为已知一次函数的函数值求对应的自变量的值;用函数的观点看二元一次方程,则以二元一次方程的解为坐标的点集就是一次函数的图象,二元一次方程组的解就是相应的两个一次函数图象(两条直线)的交点坐标,用函数的观点看一元一次不等式,它的解集就是使得函数值在某个范围的自变量的取值范围,研究函数、方程、不等式之间的联系可以深化相关知识的优化知识结构.建立这种联系的关键是建立一次函数与二元一次方程的联系.
教学目标
1.认识一次函数与一元一次方程,二元一次方程(组),一元一次不等式之间的联系,会用数点解方程和不等式及其解成解集的意义;
2.经历用函数图象表示方程和不等式的过程,进一步体会“以形表数,以数释形”的数形结合思想;
教学重难点
【重点】理解一次函数与二元一次方程(组)的联系.
【难点】把一次函数图象上点的坐标与方程(组)的解建立联系.
教学方法
问题启发法、观察归纳法、探究法.
教学过程
(一)情境导入
今天数学王国搞了个家庭Party,各个成员按照自己所在的集合就坐,这时来了“x+y=5”.
如果是你,你会让它坐在哪儿?
意图:设置数学分类的有趣情境,让学生思考一次函数和二元一次方程之间的区别和联系,从而引入课题.
效果:引发了学生对一次函数和方程间区别与联系的思考.
新课讲授
一次函数与一元一次方程
问题1 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程 kx +b =m 就是求当函数(y=kx +b)值为m时对应的自变量的值.
练一练
1.直线y=2x+20与x轴交点坐标为(-10,0 ),这说明方程2x+20=0的解是x=-10.
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(5,_0 ).
归纳总结 一次函数与一元一次方程的关系
意图:运用平面直角坐标系,将函数图象和函数值相对应,让学生从函数的角度去理解方程的解,将一次函数和方程相联系,体会数形结合的思想.
效果:学生理解了解方程的解就是已知函数值求自变量的值.
2.一次函数与一元一次不等式
问题2 下面三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b的函数值小于c的对应的自变量取值范围.
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3?
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
(2)由图象可知,当x>1时,y<3.
归纳总结 一次函数与一元一次不等式的关系
意图:比照研究一次函数与方程的关系,从函数图象出发来比较两条直线上函数值的大小,从而得出自变量的取值范围,即是不等式的解集,使学生对数形结合思想加深理解.
效果:学生明白了一次函数与一元一次不等式的关系,学会了如何从函数图象上求一元一次不等式的解集.
3.一次函数与二元一次方程组
问题3 1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气球所在位置的海拔 y(m)与气球上升时间 x(min)的函数关系.
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
思考1:一次函数与二元一次方程有什么关系?
从式子(数)角度看:
思考2:从形的角度看,一次函数与二元一次方程有什么关系?
由函数图象的定义可知:
直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解
(2)什么时刻,1号气球的高度赶上2 号气球的高度?这时的高度是多少?请从数和形两方面分别加以研究.
从数的角度看:
解方程组
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
从形的角度看,二元一次方程组与一次函数有什么关系?
二元一次方程组的解就是相应的两个一次函数图象的交点坐标.
归纳总结 一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
意图:让学生用方程观点看一次函数,发现一次函数的表达式是一个二元一次方程.引导学生用函数的观点,从数和形两方面深化对二元一次方程组解的认识.通过式子之间的转换,让学生体会只要把未知数和变量的角色互换,则二元一次方程与一次函数也实现了互相转化.
效果:学生理解了一次函数与二元一次方程(组)间的联系,再次体会了数形结合思想.
观察函数图象,直接回答下列问题:
(1)在什么时候,1 号气球比2 号气球高?
(2)在什么时候,2 号气球比1 号气球高?
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
解:(1)20min后,1 号气球比2 号气球高.
(2)0~20min时,1 号气球比2 号气球高.
例2 如图,求直线l1与l2 的交点坐标.
分析:由函数图象可以求直线l1与l2的解析式,进而通过方程组求出交点坐标.
解:因为直线l1过点(-1,0),(0,2) ,用待定系数法可求得直线l1的解析式为y =2x+2.同理可求得直线l2的解析式为y =-x+3.
解方程组得
即直线l1与l2的交点坐标为
练一练 如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组的解是多少?
解:此方程组的解是
课堂练习
1.一次函数y=kx+3的图象如图所示,则方程kx+3=0的解为x=-3.
若方程组的解为,则一次函数y=2x+1与y=3x-1的图象交点坐标为(2,5).
小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象 l1.l2如图 ,他解的这个方程组是( D )
4.一次函数y1=4x+5与y2=3x+10的图象如图所示,则4x+5>3x+10的解集是( B )
A.x<5
B.x>5
C.x>-5
D.x>25
意图:加深对一次函数与方程(组)、不等式的理解,巩固数形结合思想.
效果:检测了学生对本节课知识的掌握和运用情况.
(四)课堂小结
教师引导学生回顾本节课所学的主要内容,通过相互交流分享观点:
1. 一次函数与一元一次方程:
对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
2.一次函数与一元一次不等式:
对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
3.一次函数与二元一次方程组:
求对应两条直线交点的坐标 .
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能,培养提升数学素养.
效果:学生对本节课所学知识有了系统的回顾.
(五)作业布置
完成配套练习
板书设计
19.2.3一次函数与方程、不等式
1. 一次函数与一元一次方程:
对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
2.一次函数与一元一次不等式:
对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
3.一次函数与二元一次方程组:
求对应两条直线交点的坐标 .
教学反思
学生已经分别学习过一次函数、一元一次方程,二元一次方程组和一元一次不等式,知道它们都是刻画现实问题中数量关系的重要模型,但没有建立这些知识之间的有效联系.本节课重点是在平面直角坐标系中,利用函数图象从“数”和“形”两个方面来理解一次函数与一元一次方程、一元一次不等式、二元一次方程组之间的联系,体会从数量分析上他们是本质一样的,只是分析的角度是函数或方程的不同,从而培养学生数形结合的思想.
1
