初中数学人教版八下20.1.1(第2课时)平均数的应用教案
文档属性
| 名称 | 初中数学人教版八下20.1.1(第2课时)平均数的应用教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 20:08:39 | ||
图片预览


文档简介
20.1.1(第2课时)平均数的应用
教学内容分析
本课是在学习了算术平均数和加权平均数的基础上,结合具体实例,通过用样本估计总体的方法,进一步学习平均数在不同的问题中如何运用,尤其是用样本平均数估计总体平均数的方法具有很大的现实意义.
二、教学目标
1.理解组中值的意义,能利用组中值计算一组数据的加权平均数.
2.会用计算器求一组数据的加权平均数.
3.理解用样本的平均数估计总体的平均数的意义.
三、教学重难点
【重点】根据频数分布表求加权平均数,理解样本平均数的统计意义..
【难点】根据频数分布表求加权平均数.
四、教学方法
问题启发法、观察归纳法、探究法.
五、教学过程
(一)复习导入
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则叫做这n个数的加权平均数.
2.在求一组数据的平均数时,某个数据出现的次数看作是这个数的权 .
意图:通过对上节课内容的回顾,巩固了权和加权平均数的概念理解,为本节课的学习奠定了知识基础,引入了本节课题.
效果:学生们通过回顾旧知为本节课的学习进行了知识储备.
新课讲授
组中值与平均数
问题1: 为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
分析:表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
知识要点:(1)数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
1≤x<21的组中值为
(2)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
解:这天5路公共汽车平均每班的载客量是
x=
≈73(人).
意图:让学生在思考问题的过程中,理解表中所表达出来的信息,培养学生分析数据的能力,体会利用统计知识解决生活中的实际问题.
效果:学生理解了可以用组中值来进行数据的统计分析.
使用计算器说明:
(1)不同品牌的计算器的操作步骤有所不同,操作时需要参阅计算器的使用说明书.
(2)通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f1, f2,…,fn ;
最后按动求平均数的功能键(例如键),计算器便会求出平均数的值.
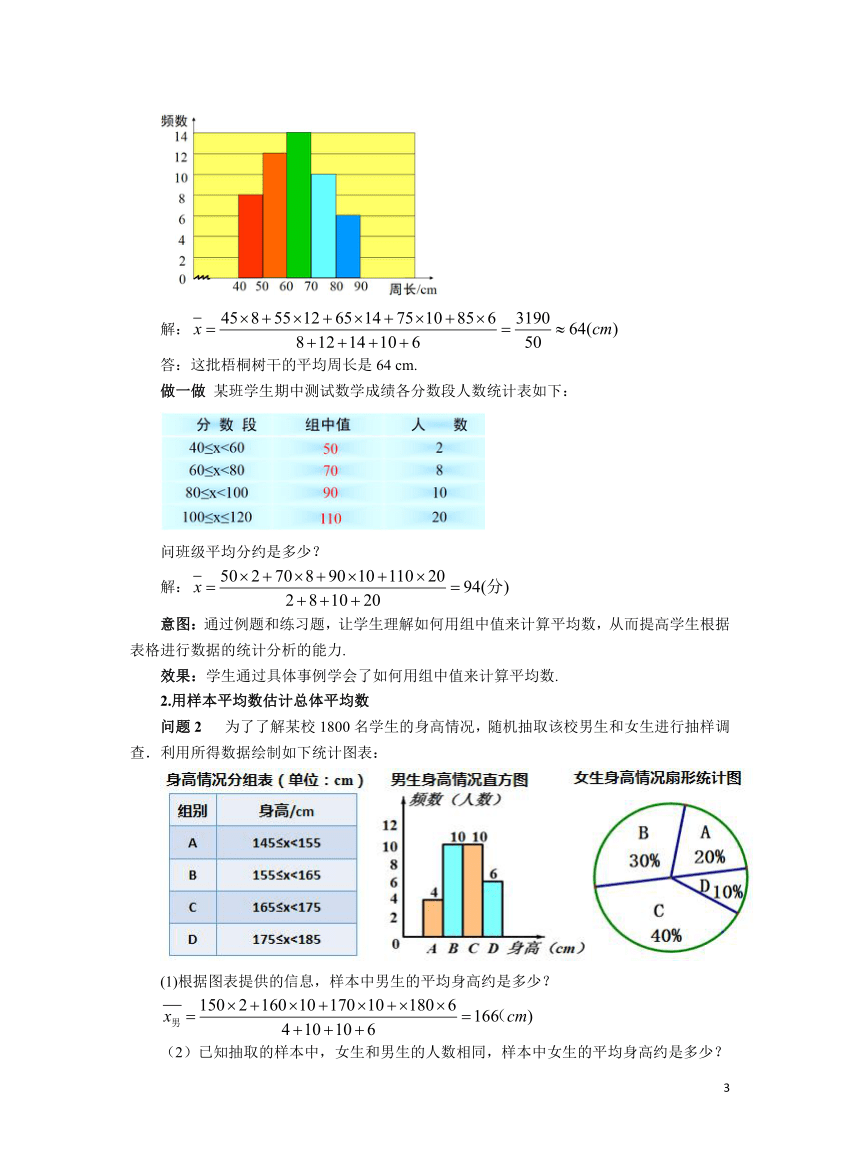
例1 为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
解:
答:这批梧桐树干的平均周长是64 cm.
做一做 某班学生期中测试数学成绩各分数段人数统计表如下:
问班级平均分约是多少?
解:
意图:通过例题和练习题,让学生理解如何用组中值来计算平均数,从而提高学生根据表格进行数据的统计分析的能力.
效果:学生通过具体事例学会了如何用组中值来计算平均数.
2.用样本平均数估计总体平均数
问题2 为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
(3)若抽样的女生为m人,女生的平均身高会改变吗?若改变,请计算;若不变,请说明理由.
(4)根据以上结果,你能估计该校女生的平均身高吗?
用样本的平均数可以估计总体的平均数.
意图:通过生活实际问题,引导学生学会如何从各种统计图表中提取信息,计算出样本的平均数,进而用样本平均数估计总体平均数,增强学生的数据分析能力.
效果:学生学会了读取统计表格中的信息,和用样本平均数估计总体平均数.
例2 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
解析:抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是1 672 h.
做一做 种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜.
解:
答:估计这个新品种黄瓜平均每株约结13根黄瓜.
课堂练习
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
2.某班40名学生身高情况如下图,请计算该班学生平均身高.
解:
答:该班学生平均身高为165.5cm.
3.为了检查一批零件的质量,从中随机抽取10件,
测得它们的长度(单位:mm)如下:
22.36 22.35 22.33 22.35 22.37
22.34 22.38 22.36 22.32 22.35
根据以上数据,估计这批零件的平均长度.
解:根据以上数据,得
即样本平均数为 22.351
答:这批零件的平均长度大约是22.351mm.
4.下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
本次测验的平均分约是多少?
已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:(1)∵点D,O,E在同一条直线上,∴∠ DOE=180°,
∴60≤x<80所占百分比为 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%
=60(分)
(2)设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
意图:巩固学生用样本平均数估计总体平均数的知识解决问题,并体会统计中数据分析的乐趣.
效果:检测了学生对应用平均数解决数据分析问题的能力.
课堂小结
引导学生回顾本节课所学内容,谈谈自己的收获.
1.组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
2.用计算器求平均数
3.用样本平均数估计总体平均数
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能.
效果:学生对本节课所学知识有了系统的回顾.
作业布置
完成配套练习
板书设计
20.1.1平均数的应用
1.组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
2.用计算器求平均数
3.用样本平均数估计总体平均数
七、教学反思
首先复习加权平均数的概念,温故知新. 之后教师结合一系列的生活实例,引导学生从统计图表中提取数据信息,并进一步探究组中值与平均数的关系,学会用组中值来计算样本的平均数.在此基础上,理解“估计”的意思,使用样本平均数估计总体平均数.本节课主要是让学生经历用平均数解决实际问题的过程,体会平均数的统计意义和应用价值,提高学生的数据分析能力.
1
教学内容分析
本课是在学习了算术平均数和加权平均数的基础上,结合具体实例,通过用样本估计总体的方法,进一步学习平均数在不同的问题中如何运用,尤其是用样本平均数估计总体平均数的方法具有很大的现实意义.
二、教学目标
1.理解组中值的意义,能利用组中值计算一组数据的加权平均数.
2.会用计算器求一组数据的加权平均数.
3.理解用样本的平均数估计总体的平均数的意义.
三、教学重难点
【重点】根据频数分布表求加权平均数,理解样本平均数的统计意义..
【难点】根据频数分布表求加权平均数.
四、教学方法
问题启发法、观察归纳法、探究法.
五、教学过程
(一)复习导入
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则叫做这n个数的加权平均数.
2.在求一组数据的平均数时,某个数据出现的次数看作是这个数的权 .
意图:通过对上节课内容的回顾,巩固了权和加权平均数的概念理解,为本节课的学习奠定了知识基础,引入了本节课题.
效果:学生们通过回顾旧知为本节课的学习进行了知识储备.
新课讲授
组中值与平均数
问题1: 为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
分析:表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
知识要点:(1)数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
1≤x<21的组中值为
(2)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
解:这天5路公共汽车平均每班的载客量是
x=
≈73(人).
意图:让学生在思考问题的过程中,理解表中所表达出来的信息,培养学生分析数据的能力,体会利用统计知识解决生活中的实际问题.
效果:学生理解了可以用组中值来进行数据的统计分析.
使用计算器说明:
(1)不同品牌的计算器的操作步骤有所不同,操作时需要参阅计算器的使用说明书.
(2)通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f1, f2,…,fn ;
最后按动求平均数的功能键(例如键),计算器便会求出平均数的值.
例1 为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
解:
答:这批梧桐树干的平均周长是64 cm.
做一做 某班学生期中测试数学成绩各分数段人数统计表如下:
问班级平均分约是多少?
解:
意图:通过例题和练习题,让学生理解如何用组中值来计算平均数,从而提高学生根据表格进行数据的统计分析的能力.
效果:学生通过具体事例学会了如何用组中值来计算平均数.
2.用样本平均数估计总体平均数
问题2 为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
(3)若抽样的女生为m人,女生的平均身高会改变吗?若改变,请计算;若不变,请说明理由.
(4)根据以上结果,你能估计该校女生的平均身高吗?
用样本的平均数可以估计总体的平均数.
意图:通过生活实际问题,引导学生学会如何从各种统计图表中提取信息,计算出样本的平均数,进而用样本平均数估计总体平均数,增强学生的数据分析能力.
效果:学生学会了读取统计表格中的信息,和用样本平均数估计总体平均数.
例2 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
解析:抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是1 672 h.
做一做 种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜.
解:
答:估计这个新品种黄瓜平均每株约结13根黄瓜.
课堂练习
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
2.某班40名学生身高情况如下图,请计算该班学生平均身高.
解:
答:该班学生平均身高为165.5cm.
3.为了检查一批零件的质量,从中随机抽取10件,
测得它们的长度(单位:mm)如下:
22.36 22.35 22.33 22.35 22.37
22.34 22.38 22.36 22.32 22.35
根据以上数据,估计这批零件的平均长度.
解:根据以上数据,得
即样本平均数为 22.351
答:这批零件的平均长度大约是22.351mm.
4.下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
本次测验的平均分约是多少?
已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:(1)∵点D,O,E在同一条直线上,∴∠ DOE=180°,
∴60≤x<80所占百分比为 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%
=60(分)
(2)设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
意图:巩固学生用样本平均数估计总体平均数的知识解决问题,并体会统计中数据分析的乐趣.
效果:检测了学生对应用平均数解决数据分析问题的能力.
课堂小结
引导学生回顾本节课所学内容,谈谈自己的收获.
1.组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
2.用计算器求平均数
3.用样本平均数估计总体平均数
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学知识和技能.
效果:学生对本节课所学知识有了系统的回顾.
作业布置
完成配套练习
板书设计
20.1.1平均数的应用
1.组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
2.用计算器求平均数
3.用样本平均数估计总体平均数
七、教学反思
首先复习加权平均数的概念,温故知新. 之后教师结合一系列的生活实例,引导学生从统计图表中提取数据信息,并进一步探究组中值与平均数的关系,学会用组中值来计算样本的平均数.在此基础上,理解“估计”的意思,使用样本平均数估计总体平均数.本节课主要是让学生经历用平均数解决实际问题的过程,体会平均数的统计意义和应用价值,提高学生的数据分析能力.
1
