4.3.2对数的运算(两个课时) 课件(共36张PPT)
文档属性
| 名称 | 4.3.2对数的运算(两个课时) 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 11:00:51 | ||
图片预览











文档简介
(共36张PPT)
章节:第四章指数函数与对数函数
标题:4.3.2对数的运算
课时:2课时
目
录
行业PPT模板http:///hangye/
1.教学目标
2.新课讲授
3.新课小结
4.作业巩固
PART 01
教学目标
环节1:教学目标分解
教学目标 素养目标
1.理解对数函数的概念和运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数. 数学抽象数学运算
逻辑推理
直观想象
数学建模
2.通过具体实例,了解对数函数的概念,能借助描点法或借助计算工具画出具体对数函数的图像,探索并了解对数函数的单调性与特殊点.
3.知道对数函数与指数函数互为反函数.
4.能够应用对数函数的图像及性质解决问题
环节2:教学重难点
重点、难点:
1.理解对数运算性质
2.知道用换底公式能将一般对数转化成自然对数或常用对数
PART 02
新课讲授
1.复习回顾
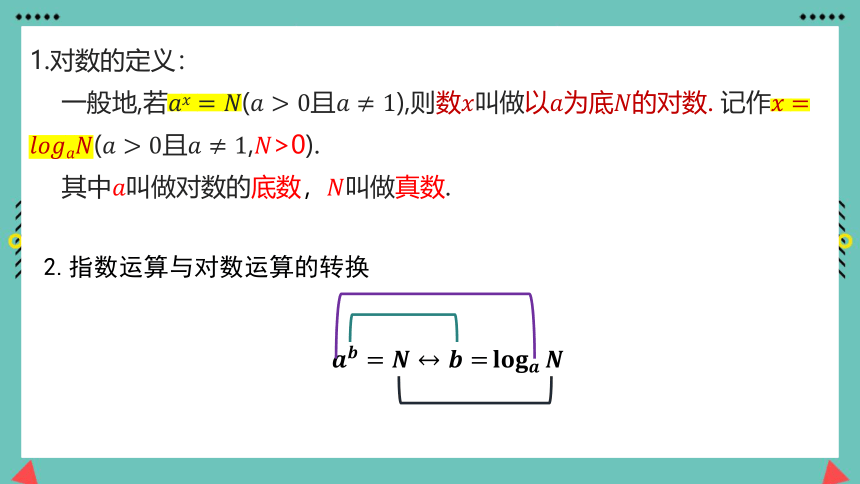
1.对数的定义:
一般地,若(且),则数叫做以为底的对数. 记作(,>0).
其中叫做对数的底数,叫做真数.
2.指数运算与对数运算的转换
指数的运算性质是怎样的?
指数运算性质:
(1);
(2);
(3)
在引入对数后,自然应研究对数的运算性质.你认为可以怎样研究?
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
2.对数的积、商、幂的运算性质
情景一:
由指数幂的运算性质:
问题1 我们能推导出怎样的对数运算性质
令,
,由对数与指数之间的关系得:
因此, .
(1)
真数相乘,对数相加
问题2 由指数幂的运算性质:,我们能推导出怎样的对数运算性质
令, ,则.
由对数与指数之间的关系得:
,
因此, .
(2)
真数相除,对数相减
问题3 由指数幂的运算性质:,我们能推导出怎样的对数运算性质
令,则
由对数与指数之间的关系得:
,
因此,
(3)
真数的幂等于对数的系数
概念1:
(1)
(2)
(3);
课堂例题
例3 求下列各式的值:
解
.
例4 用表示:
课堂例题
解:
.
数学史上,人们经过大量努力,制作了常用对数表和自然对数表,只要通过查表就可以求出任意正数的常用对数或自然对数.现在,利用计算工具,也可以直接求出任意正数的常用对数或自然对数.这样,如果能将其他底的对数转换为以10或为底的对数,就能方便地求出这些对数.
问题4:(1)利用计算工具求的近似值;
(2)根据对数的定义,你能利用的值求的值吗?
(3)根据对数的定义,你能用表示吗?
...(课后,大家可以利用数学计算器将常见的特殊对数值进行记录。)
根据对数的定义,你能利用吗?
令,则
等式两边同时取对数得
即: 解得
概念2:
换底公式:
由换底公式得到的常用结论:
① ②
③; ④.
课堂例题
例5 尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为
年月日,日本东北部海域发生里氏级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏级地震的多少倍(精确到1)?
解:设里氏级和级地震的能量分别为和.
由题已知:
解
PART 03
新课小结
1.对数的运算性质:
(1)
(2)
(3);
2.换底公式:
由换底公式得到的常用结论:
① ②
③; ④.
PART 04
作业巩固
课本P126练习
课本P126练习
课本P126练习
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
非常感谢您的观看
章节:第四章指数函数与对数函数
标题:4.3.2对数的运算
课时:2课时
目
录
行业PPT模板http:///hangye/
1.教学目标
2.新课讲授
3.新课小结
4.作业巩固
PART 01
教学目标
环节1:教学目标分解
教学目标 素养目标
1.理解对数函数的概念和运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数. 数学抽象数学运算
逻辑推理
直观想象
数学建模
2.通过具体实例,了解对数函数的概念,能借助描点法或借助计算工具画出具体对数函数的图像,探索并了解对数函数的单调性与特殊点.
3.知道对数函数与指数函数互为反函数.
4.能够应用对数函数的图像及性质解决问题
环节2:教学重难点
重点、难点:
1.理解对数运算性质
2.知道用换底公式能将一般对数转化成自然对数或常用对数
PART 02
新课讲授
1.复习回顾
1.对数的定义:
一般地,若(且),则数叫做以为底的对数. 记作(,>0).
其中叫做对数的底数,叫做真数.
2.指数运算与对数运算的转换
指数的运算性质是怎样的?
指数运算性质:
(1);
(2);
(3)
在引入对数后,自然应研究对数的运算性质.你认为可以怎样研究?
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢?
2.对数的积、商、幂的运算性质
情景一:
由指数幂的运算性质:
问题1 我们能推导出怎样的对数运算性质
令,
,由对数与指数之间的关系得:
因此, .
(1)
真数相乘,对数相加
问题2 由指数幂的运算性质:,我们能推导出怎样的对数运算性质
令, ,则.
由对数与指数之间的关系得:
,
因此, .
(2)
真数相除,对数相减
问题3 由指数幂的运算性质:,我们能推导出怎样的对数运算性质
令,则
由对数与指数之间的关系得:
,
因此,
(3)
真数的幂等于对数的系数
概念1:
(1)
(2)
(3);
课堂例题
例3 求下列各式的值:
解
.
例4 用表示:
课堂例题
解:
.
数学史上,人们经过大量努力,制作了常用对数表和自然对数表,只要通过查表就可以求出任意正数的常用对数或自然对数.现在,利用计算工具,也可以直接求出任意正数的常用对数或自然对数.这样,如果能将其他底的对数转换为以10或为底的对数,就能方便地求出这些对数.
问题4:(1)利用计算工具求的近似值;
(2)根据对数的定义,你能利用的值求的值吗?
(3)根据对数的定义,你能用表示吗?
...(课后,大家可以利用数学计算器将常见的特殊对数值进行记录。)
根据对数的定义,你能利用吗?
令,则
等式两边同时取对数得
即: 解得
概念2:
换底公式:
由换底公式得到的常用结论:
① ②
③; ④.
课堂例题
例5 尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为
年月日,日本东北部海域发生里氏级地震,它所释放出来的能量是2008年5月12日我国汶川发生里氏级地震的多少倍(精确到1)?
解:设里氏级和级地震的能量分别为和.
由题已知:
解
PART 03
新课小结
1.对数的运算性质:
(1)
(2)
(3);
2.换底公式:
由换底公式得到的常用结论:
① ②
③; ④.
PART 04
作业巩固
课本P126练习
课本P126练习
课本P126练习
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
课本P126 习题4.3
非常感谢您的观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
