18.3一次函数的性质
图片预览





文档简介
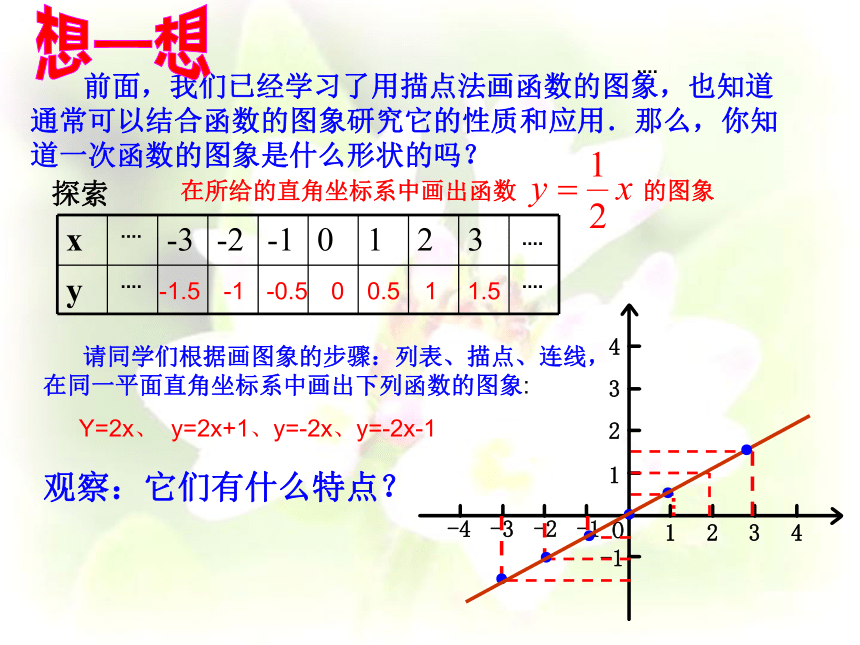
课件26张PPT。 一次函数的性质 前面,我们已经学习了用描点法画函数的图象,也知道通常可以结合函数的图象研究它的性质和应用.那么,你知道一次函数的图象是什么形状的吗? 想一想在所给的直角坐标系中画出函数 的图象探索 -1.5-1-0.500.511.5●●●●●● 请同学们根据画图象的步骤:列表、描点、连线,
在同一平面直角坐标系中画出下列函数的图象: Y=2x、 y=2x+1、y=-2x、y=-2x-1观察:它们有什么特点? 概括:1.一次函数y = kx + b的图象是什么图形?你是通过确定几个点来作一次函数y=kx+b的图象的呢?2.求作函数的图象。y=kx+b的图象是一条直线;两个点。(1)正比例函数y=kx的图象有什么特点?(2)你作正比例函数y=kx的图象时描了几个点想
一
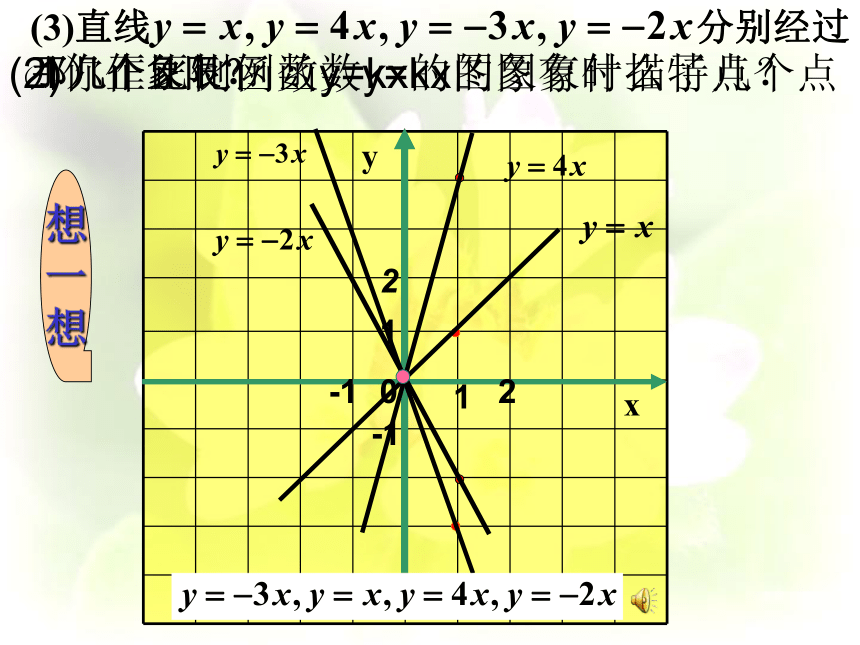
想021-1-121归纳总结:一、正比例函数y = kx (k≠0)图象的性质1、正比例函数 y = kx 的图象都是经过坐标原点(0,0)的一条直线;
2、(1)当 k>0时,y=kx经过一、三象限,
(2)当 k<0时,y=kx经过二、四象限;1.一次函数y=(-3k+1)x+2k-1
的图象经过原点,试确定
k的值。 2.(2001.杭州)如果正比例函数y=(m-3)x经过第一、三象限,则m的取值范围_______. 小试牛刀:-3k+1≠0,
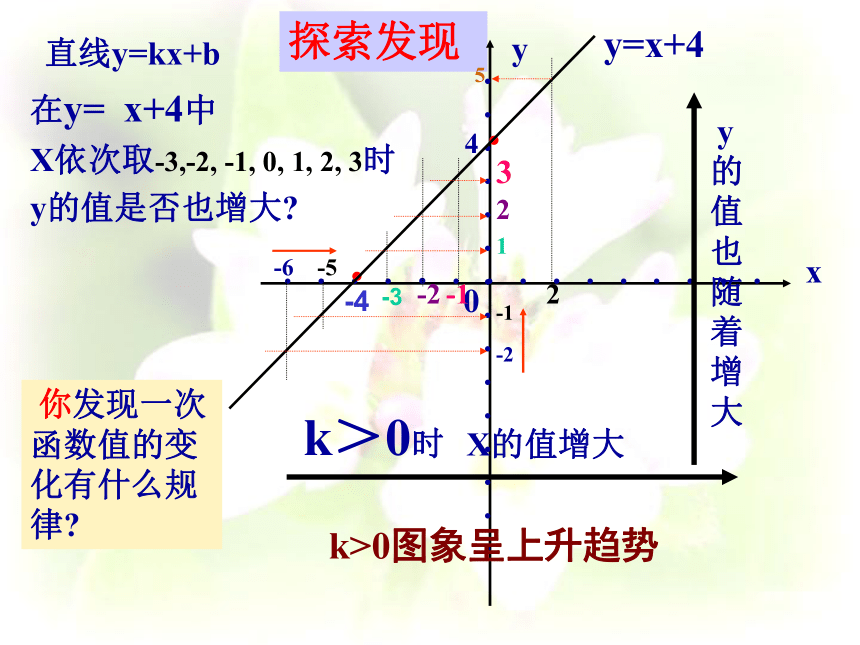
2k-1=0.∵m-3>0∴m>3m>3探索发现对一次函数y=x+4,x依次取-3,-2,-1,0,1,2,3
逐渐增大的过程中,y的值是否也在增大?
对y=-x+4呢?1234 5 6 77654 3 2 1y增大y减小直线y=kx+b在y= x+4中
X依次取-3,-2, -1, 0, 1, 2, 3时
y的值是否也增大?探索发现
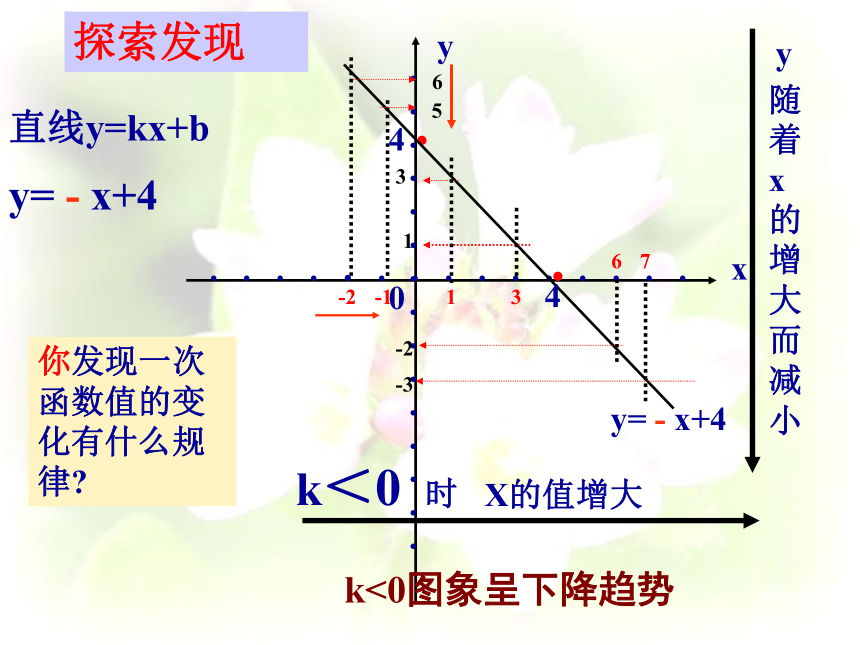
··y=x+4 你发现一次函数值的变化有什么规律?4k>0图象呈上升趋势-4-3直线y=kx+by= - x+4探索发现
··你发现一次函数值的变化有什么规律?4k<0图象呈下降趋势4归纳总结:当k<0时,y的值随着x值的增大而减小,图象呈上升趋势;图象呈下降趋势。学 以 致 用下列函数,y的值随着x值的增大如何变化?增大减小增大减小2、写出m的3个值,使相应的
一次函数y=(2m-1)x+2的值都
是随着x值的增大而减小.2m-1<0-6 -4 -2 0 2 4 6-6+2-4+2-2+20+22+24+26+2试一试:在同一直角坐标系中画出y=2x和y=2x+2的图象1、列表······2、描点3、连线y=2x-3 (-3,-4) (-2,-2) (-1,0)
(0,2)(1,4) (2,6) (3,8)猜一猜:函数y=2x-3的图象是怎样的?y=2xy=2x+2结论:
在直线y=k1x+b1与直线y=k2x+b2中,
如果k1 = k2 , b1≠b2那么这两条直线平行。22·y=2x+2可由y=2x向上平移2个单位得到将y =2x向下平移3个单位得到想一想:在同一坐标系中画出y=2x,y=2x+2和y=2x-3的图象y=2x-3那么:函数y=2x+b的图象是怎样得到的?y=2xy=2x+2y=kx+b可由y=kx向上或者向下平移得到。·y=2x+2可由y=2x向上平移2个单位得到y=2x-3可由y =2x向下平移3个单位得到函数y=kx+b能由y=kx得到吗?b>0,向上平移;b<0,向下平移。y=2x经过那些象限?
y=2x+2呢?
y=2x-3呢?
当k>0时,y=kx+b呢?一、二、三一、三、四一、三归纳总结:k>0b>0b<0一、三、一、三、k<0b>0b<0 二、四、二、四、xyoy = - 2x - 3y = -2x + 1y = 2x + 1y=2x-2y=2xk<0k>0二四一三练习1 已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B挑 战 自 我练习2 1、若直线 y =mx+n经过第一、 二、三象)限,讨论m、n的符号。m>0,n>0挑 战 自 我 2、直线 分别是由直线经过怎样的移动得到的. 分析:只要k相同,直线就平行,一次函数y=kx+b(k≠0)是由正比例函数的图象y=kx(k≠0)经过向上或向下平移个单位得到的.b>0,直线向上移;b<0,直线向下移. 解: 是由直线 向上平移3个单位得到的;而是由直线向下平移5个单位得到的. 练习3一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )挑 战 自 我ABCDA 4、一次函数y=kx+b的图象如图所示,则
k 0,b 0 xyo<<挑 战 自 我 1、y=|x|中,x y的函数,y x 的函数(填“是”或“不是”),图象为 不是是 2、某企业去年积压产品a件(a>0),今年预计每月销售产
品2b件,同时每月可生产出产品b个,若产品积压量y(件)
是今年开工时间(月)的函数,则它的图象只能是( )练习DC3、拖拉机开始工作时,油箱中有油24L,可用6小时。那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x ?
C例3. 如图,l1反映了某公司产品的销售收入与销售量的关系,(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000 l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;4吨(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨小于4吨一次函数的性质 1.在y=kx+b中:
当k>0,y随x的增大而______;当k<0,y随x的增大而______.正比例函数的性质1.正比例函数y=kx的图象是
经过_________的一条直线;2.在直线y=k1x+b1与直线y=k2x+b2中,
如果______________,那么这两条直线平行。 2. 1)当 k >0,y=kx经过______象限
2)当 k <0,y=kx经过______象限.颗粒归仓k1 = k2 , b1≠b2增大减小原点(0,0)一、三二、四3.y=kx+b(k≠0)所经过的象限:k>0,b>0→___ ___ ___k>0,b<0→___ ___ ___k<0,b>0→___ ___ ___ k<0,b<0→___ ___ ___一、三、二一、三、四二、四、一二、四、三作业:P42:1、2 ;
P47:习题4、5、
在同一平面直角坐标系中画出下列函数的图象: Y=2x、 y=2x+1、y=-2x、y=-2x-1观察:它们有什么特点? 概括:1.一次函数y = kx + b的图象是什么图形?你是通过确定几个点来作一次函数y=kx+b的图象的呢?2.求作函数的图象。y=kx+b的图象是一条直线;两个点。(1)正比例函数y=kx的图象有什么特点?(2)你作正比例函数y=kx的图象时描了几个点想
一
想021-1-121归纳总结:一、正比例函数y = kx (k≠0)图象的性质1、正比例函数 y = kx 的图象都是经过坐标原点(0,0)的一条直线;
2、(1)当 k>0时,y=kx经过一、三象限,
(2)当 k<0时,y=kx经过二、四象限;1.一次函数y=(-3k+1)x+2k-1
的图象经过原点,试确定
k的值。 2.(2001.杭州)如果正比例函数y=(m-3)x经过第一、三象限,则m的取值范围_______. 小试牛刀:-3k+1≠0,
2k-1=0.∵m-3>0∴m>3m>3探索发现对一次函数y=x+4,x依次取-3,-2,-1,0,1,2,3
逐渐增大的过程中,y的值是否也在增大?
对y=-x+4呢?1234 5 6 77654 3 2 1y增大y减小直线y=kx+b在y= x+4中
X依次取-3,-2, -1, 0, 1, 2, 3时
y的值是否也增大?探索发现
··y=x+4 你发现一次函数值的变化有什么规律?4k>0图象呈上升趋势-4-3直线y=kx+by= - x+4探索发现
··你发现一次函数值的变化有什么规律?4k<0图象呈下降趋势4归纳总结:当k<0时,y的值随着x值的增大而减小,图象呈上升趋势;图象呈下降趋势。学 以 致 用下列函数,y的值随着x值的增大如何变化?增大减小增大减小2、写出m的3个值,使相应的
一次函数y=(2m-1)x+2的值都
是随着x值的增大而减小.2m-1<0-6 -4 -2 0 2 4 6-6+2-4+2-2+20+22+24+26+2试一试:在同一直角坐标系中画出y=2x和y=2x+2的图象1、列表······2、描点3、连线y=2x-3 (-3,-4) (-2,-2) (-1,0)
(0,2)(1,4) (2,6) (3,8)猜一猜:函数y=2x-3的图象是怎样的?y=2xy=2x+2结论:
在直线y=k1x+b1与直线y=k2x+b2中,
如果k1 = k2 , b1≠b2那么这两条直线平行。22·y=2x+2可由y=2x向上平移2个单位得到将y =2x向下平移3个单位得到想一想:在同一坐标系中画出y=2x,y=2x+2和y=2x-3的图象y=2x-3那么:函数y=2x+b的图象是怎样得到的?y=2xy=2x+2y=kx+b可由y=kx向上或者向下平移得到。·y=2x+2可由y=2x向上平移2个单位得到y=2x-3可由y =2x向下平移3个单位得到函数y=kx+b能由y=kx得到吗?b>0,向上平移;b<0,向下平移。y=2x经过那些象限?
y=2x+2呢?
y=2x-3呢?
当k>0时,y=kx+b呢?一、二、三一、三、四一、三归纳总结:k>0b>0b<0一、三、一、三、k<0b>0b<0 二、四、二、四、xyoy = - 2x - 3y = -2x + 1y = 2x + 1y=2x-2y=2xk<0k>0二四一三练习1 已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B挑 战 自 我练习2 1、若直线 y =mx+n经过第一、 二、三象)限,讨论m、n的符号。m>0,n>0挑 战 自 我 2、直线 分别是由直线经过怎样的移动得到的. 分析:只要k相同,直线就平行,一次函数y=kx+b(k≠0)是由正比例函数的图象y=kx(k≠0)经过向上或向下平移个单位得到的.b>0,直线向上移;b<0,直线向下移. 解: 是由直线 向上平移3个单位得到的;而是由直线向下平移5个单位得到的. 练习3一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )挑 战 自 我ABCDA 4、一次函数y=kx+b的图象如图所示,则
k 0,b 0 xyo<<挑 战 自 我 1、y=|x|中,x y的函数,y x 的函数(填“是”或“不是”),图象为 不是是 2、某企业去年积压产品a件(a>0),今年预计每月销售产
品2b件,同时每月可生产出产品b个,若产品积压量y(件)
是今年开工时间(月)的函数,则它的图象只能是( )练习DC3、拖拉机开始工作时,油箱中有油24L,可用6小时。那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x ?
C例3. 如图,l1反映了某公司产品的销售收入与销售量的关系,(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000 l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;4吨(4)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);大于4吨小于4吨一次函数的性质 1.在y=kx+b中:
当k>0,y随x的增大而______;当k<0,y随x的增大而______.正比例函数的性质1.正比例函数y=kx的图象是
经过_________的一条直线;2.在直线y=k1x+b1与直线y=k2x+b2中,
如果______________,那么这两条直线平行。 2. 1)当 k >0,y=kx经过______象限
2)当 k <0,y=kx经过______象限.颗粒归仓k1 = k2 , b1≠b2增大减小原点(0,0)一、三二、四3.y=kx+b(k≠0)所经过的象限:k>0,b>0→___ ___ ___k>0,b<0→___ ___ ___k<0,b>0→___ ___ ___ k<0,b<0→___ ___ ___一、三、二一、三、四二、四、一二、四、三作业:P42:1、2 ;
P47:习题4、5、
