18.1.1 平行四边形的性质导学案
文档属性
| 名称 | 18.1.1 平行四边形的性质导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 73.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-02 10:46:06 | ||
图片预览


文档简介
18.1.1平行四边形及性质1
一、目标导学
1、理解平行四边形的定义及有关概念。
2、能根据定义探索并掌握平行四边形的对边相等、对角相等的性质、对角线互相平分。
3、了解平行四边形在实际生活中的应用,根据平行四边形的性质进行简单的计算和证明。
二、自主学习
1、平行四边形的定义: 。
平行四边形用 表示,则平行四边形ABCD记作: 。
2、联系生活实际说一说生活中的哪些图形是平行四边形?
3、 叫做两条平行线之间的距离。
三、问题探究
探究1 平行四边形的性质
1、根据定义证明“平行四边形的对边相等”
2、根据定义证明“平行四边形的对角相等”
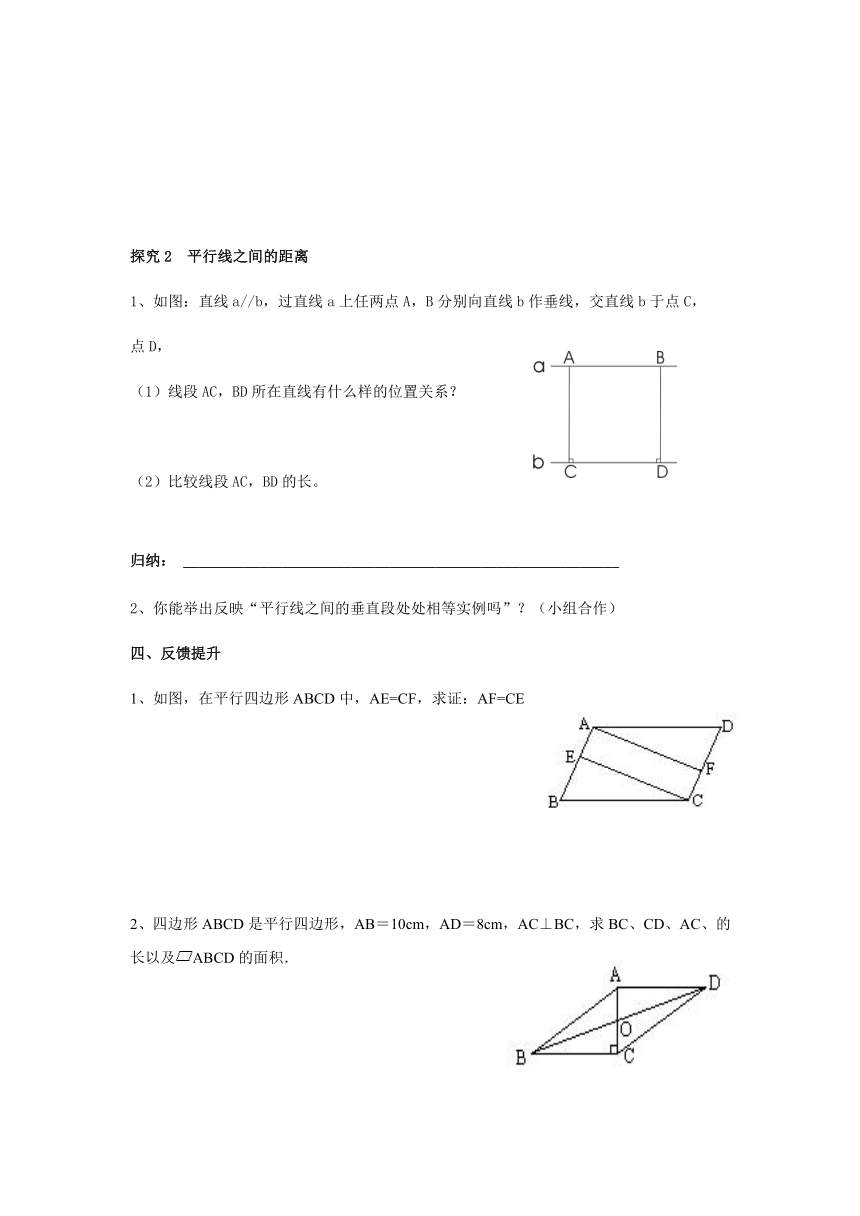
探究2 平行线之间的距离
1、如图:直线a//b,过直线a上任两点A,B分别向直线b作垂线,交直线b于点C,
点D,
(1)线段AC,BD所在直线有什么样的位置关系?
(2)比较线段AC,BD的长。
归纳: _________________________________________________________
2、你能举出反映“平行线之间的垂直段处处相等实例吗”?(小组合作)
四、反馈提升
1、如图,在平行四边形ABCD中,AE=CF,求证:AF=CE
2、四边形ABCD是平行四边形,AB=10cm,AD=8cm,AC⊥BC,求BC、CD、AC、的长以及ABCD的面积.
3、如图,已知L1//L2,AB//CD,CE⊥L2点E,FG⊥L2于点G,则下列说法中错误的是( )
AB=CD (B)CE=FG,
(C)A、B两点间的距离就是线段AB的长度
(D)L1与L2间的距离就是线段CD的长度
五、达标应用
1、填空
(1) ABCD中,AB=5,BC=3,则它的周长 。
(2) ABCD有一个内角等于40°,则另外三个内角分别为:
(3)平行四边形的周长为50cm,两邻边之比为2:3,则两邻边分别为:
(4)平行四边形的两对角和为214°,则平行四边形相邻两内角的度数分别是: .
(5)ABCD中,AB、BC、CD三边的长度为(x+3),(x-4)和16,则四边形的周长是 .
2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形,线段AD和BC的长度有什么关系?
3、如图,如果直线L1∥L2,那么△ABC的面积和△DBC的面积是相等的.你能说出理由吗 你还能在这两条平行线L1、L2之间画出其他与△ABC面积相等的三角形吗
18.1.1平行四边形的性质2
一、学习目标
1、经历探索“平行四边形的对角线互相平分”这一性质的过程,发展探究意识。
2、掌握“平行四边形的对角线互相平分”的性质定理
3、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
二、自主学习
1、 平行四边形的对角线互相 。
2、 平行四边形的对角线把 平行四边形分成的4个小三角形的面积 。
三、问题探究
探究 平行四边形对角线的性质
如图,在ABCD中,连接AC、BD交于点O,OA与OC ,OB与OD有什么关系?
证明你的结论。
由以上探索和证明,我们得到平行四边形的性质:
。
请你把上述性质用几何语言描述出来
∵四边形ABCD为
∴ = =
四、反馈提升
1、如图,ABCD的对角线AC、BD相交于点O,过点O作一条直线,分别交AB、CD于点E、F.求证:OE=OF
2、如图,在ABCD中,已知对角线AC和BD相交于点O,△BOC的周长为24,BC=10,
求对角线AC与BD的和是多少?
五、达标应用
1、在ABCD中,对角线AC、BD相交于点O,CD=6, AC=8,BD=12,
求△AOB的周长。
2、在□ABCD中,对角线AC与BD交于点O,作AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)指出图中的全等三角形
(2)求证:OF=OE
3、如图,四边形ABCD是平行四边形,DB⊥AD,求BC,CD,OB的长。
4、在ABCD中,AC=6、BD=4,则AB的取值范围是__ ______.
一、目标导学
1、理解平行四边形的定义及有关概念。
2、能根据定义探索并掌握平行四边形的对边相等、对角相等的性质、对角线互相平分。
3、了解平行四边形在实际生活中的应用,根据平行四边形的性质进行简单的计算和证明。
二、自主学习
1、平行四边形的定义: 。
平行四边形用 表示,则平行四边形ABCD记作: 。
2、联系生活实际说一说生活中的哪些图形是平行四边形?
3、 叫做两条平行线之间的距离。
三、问题探究
探究1 平行四边形的性质
1、根据定义证明“平行四边形的对边相等”
2、根据定义证明“平行四边形的对角相等”
探究2 平行线之间的距离
1、如图:直线a//b,过直线a上任两点A,B分别向直线b作垂线,交直线b于点C,
点D,
(1)线段AC,BD所在直线有什么样的位置关系?
(2)比较线段AC,BD的长。
归纳: _________________________________________________________
2、你能举出反映“平行线之间的垂直段处处相等实例吗”?(小组合作)
四、反馈提升
1、如图,在平行四边形ABCD中,AE=CF,求证:AF=CE
2、四边形ABCD是平行四边形,AB=10cm,AD=8cm,AC⊥BC,求BC、CD、AC、的长以及ABCD的面积.
3、如图,已知L1//L2,AB//CD,CE⊥L2点E,FG⊥L2于点G,则下列说法中错误的是( )
AB=CD (B)CE=FG,
(C)A、B两点间的距离就是线段AB的长度
(D)L1与L2间的距离就是线段CD的长度
五、达标应用
1、填空
(1) ABCD中,AB=5,BC=3,则它的周长 。
(2) ABCD有一个内角等于40°,则另外三个内角分别为:
(3)平行四边形的周长为50cm,两邻边之比为2:3,则两邻边分别为:
(4)平行四边形的两对角和为214°,则平行四边形相邻两内角的度数分别是: .
(5)ABCD中,AB、BC、CD三边的长度为(x+3),(x-4)和16,则四边形的周长是 .
2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形,线段AD和BC的长度有什么关系?
3、如图,如果直线L1∥L2,那么△ABC的面积和△DBC的面积是相等的.你能说出理由吗 你还能在这两条平行线L1、L2之间画出其他与△ABC面积相等的三角形吗
18.1.1平行四边形的性质2
一、学习目标
1、经历探索“平行四边形的对角线互相平分”这一性质的过程,发展探究意识。
2、掌握“平行四边形的对角线互相平分”的性质定理
3、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
二、自主学习
1、 平行四边形的对角线互相 。
2、 平行四边形的对角线把 平行四边形分成的4个小三角形的面积 。
三、问题探究
探究 平行四边形对角线的性质
如图,在ABCD中,连接AC、BD交于点O,OA与OC ,OB与OD有什么关系?
证明你的结论。
由以上探索和证明,我们得到平行四边形的性质:
。
请你把上述性质用几何语言描述出来
∵四边形ABCD为
∴ = =
四、反馈提升
1、如图,ABCD的对角线AC、BD相交于点O,过点O作一条直线,分别交AB、CD于点E、F.求证:OE=OF
2、如图,在ABCD中,已知对角线AC和BD相交于点O,△BOC的周长为24,BC=10,
求对角线AC与BD的和是多少?
五、达标应用
1、在ABCD中,对角线AC、BD相交于点O,CD=6, AC=8,BD=12,
求△AOB的周长。
2、在□ABCD中,对角线AC与BD交于点O,作AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)指出图中的全等三角形
(2)求证:OF=OE
3、如图,四边形ABCD是平行四边形,DB⊥AD,求BC,CD,OB的长。
4、在ABCD中,AC=6、BD=4,则AB的取值范围是__ ______.
