第1章丰富的图形世界 测试(含解析)2023-2024学年北师大版七年级数学上册
文档属性
| 名称 | 第1章丰富的图形世界 测试(含解析)2023-2024学年北师大版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 322.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 21:59:51 | ||
图片预览

文档简介
2023-2024学年北师大版七年级数学上册《第1章丰富的图形世界》
(附答案)
一.选择题
1.下列几何体中,属于柱体的有( )
A.1个 B.2个 C.3个 D.4个
2.将“数学核心素养”这几个字分别写在某个正方体的表面上,如图是它的一种展开图,将它折成正方体后,与“学”字所在面相对面上的汉字是( )
A.核 B.心 C.素 D.养
3.下列平面图形沿虚线旋转一周,可以得到如图所示的几何体的是( )
A. B. C. D.
4.把14个棱长为1的正方体在地面上堆叠如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为( )
A.21 B.24 C.33 D.37
5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则下列序号中不应剪去的是( )
A.6 B.3 C.2 D.1
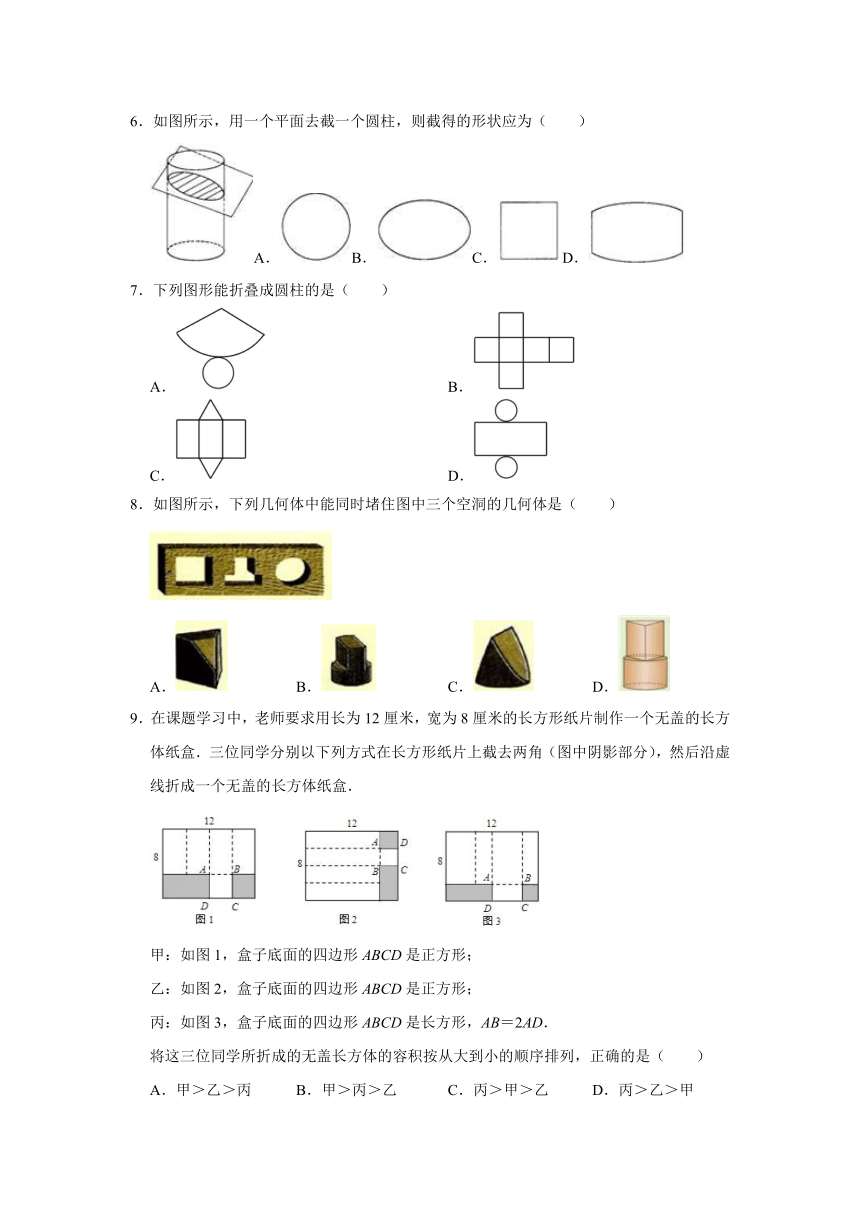
6.如图所示,用一个平面去截一个圆柱,则截得的形状应为( )
A.B.C.D.
7.下列图形能折叠成圆柱的是( )
A. B.
C. D.
8.如图所示,下列几何体中能同时堵住图中三个空洞的几何体是( )
A. B. C. D.
9.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是( )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
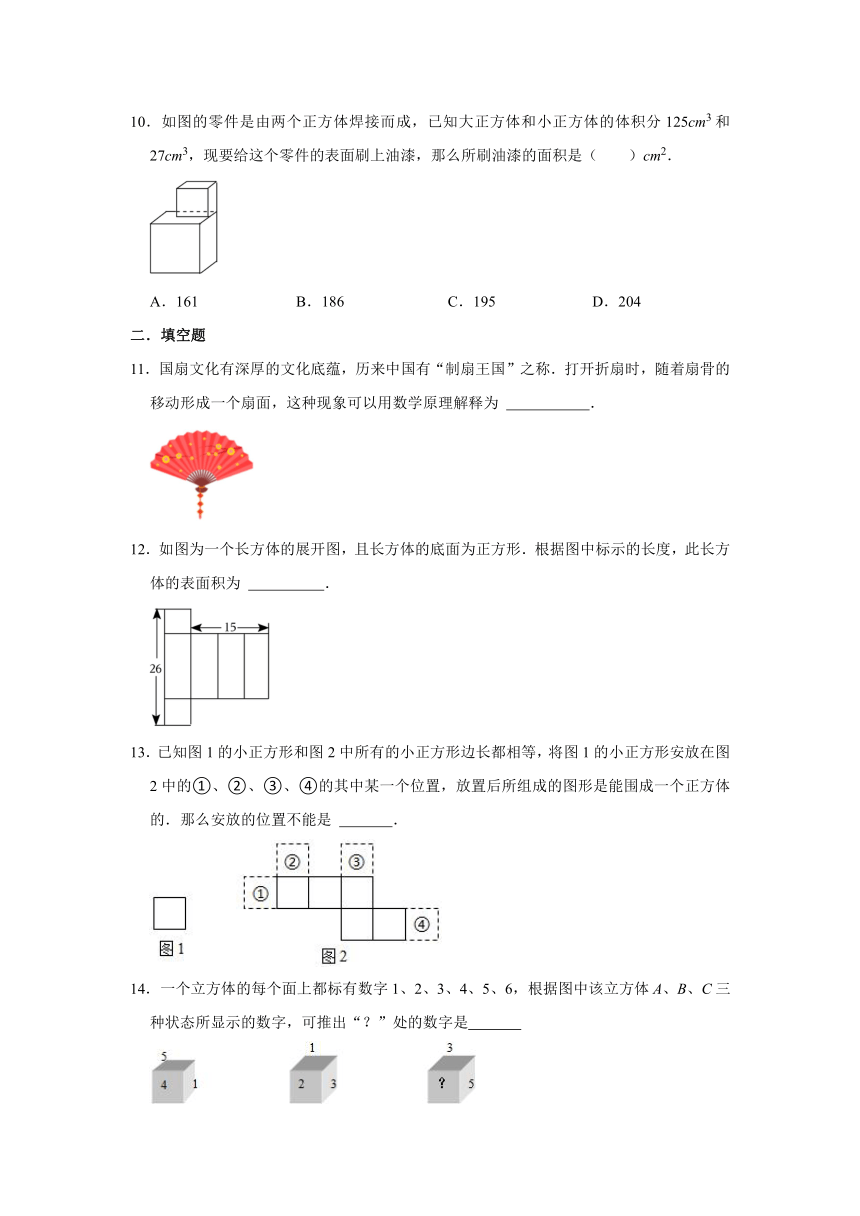
10.如图的零件是由两个正方体焊接而成,已知大正方体和小正方体的体积分125cm3和27cm3,现要给这个零件的表面刷上油漆,那么所刷油漆的面积是( )cm2.
A.161 B.186 C.195 D.204
二.填空题
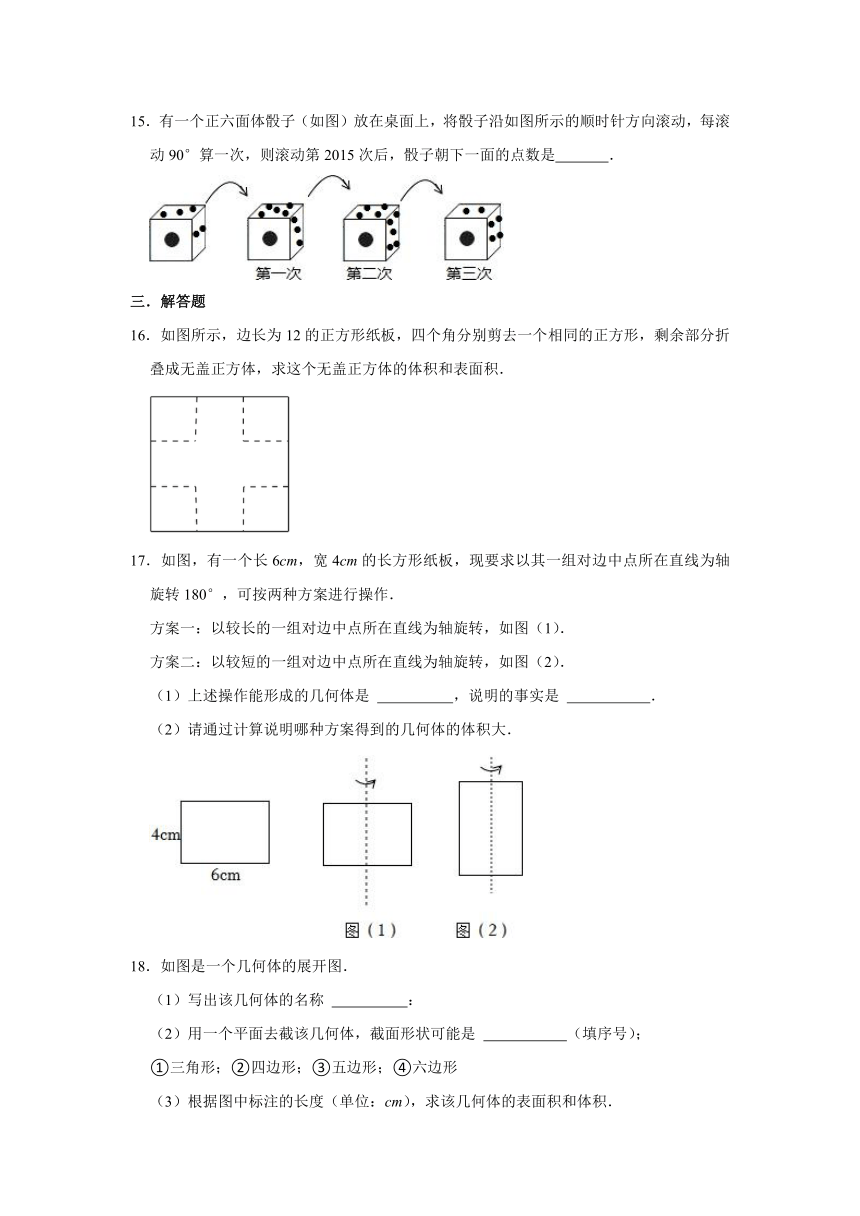
11.国扇文化有深厚的文化底蕴,历来中国有“制扇王国”之称.打开折扇时,随着扇骨的移动形成一个扇面,这种现象可以用数学原理解释为 .
12.如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,此长方体的表面积为 .
13.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是能围成一个正方体的.那么安放的位置不能是 .
14.一个立方体的每个面上都标有数字1、2、3、4、5、6,根据图中该立方体A、B、C三种状态所显示的数字,可推出“?”处的数字是
15.有一个正六面体骰子(如图)放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2015次后,骰子朝下一面的点数是 .
三.解答题
16.如图所示,边长为12的正方形纸板,四个角分别剪去一个相同的正方形,剩余部分折叠成无盖正方体,求这个无盖正方体的体积和表面积.
17.如图,有一个长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴旋转180°,可按两种方案进行操作.
方案一:以较长的一组对边中点所在直线为轴旋转,如图(1).
方案二:以较短的一组对边中点所在直线为轴旋转,如图(2).
(1)上述操作能形成的几何体是 ,说明的事实是 .
(2)请通过计算说明哪种方案得到的几何体的体积大.
18.如图是一个几何体的展开图.
(1)写出该几何体的名称 :
(2)用一个平面去截该几何体,截面形状可能是 (填序号);
①三角形;②四边形;③五边形;④六边形
(3)根据图中标注的长度(单位:cm),求该几何体的表面积和体积.
19.淘气家打算在一块长16m,宽4m的长方形菜地上搭建一个半圆柱形蔬菜棚,并全部盖上塑料薄膜(如图),这个蔬菜棚至少要用多少平方米的塑料薄膜?
20.(1)如图所示的长方体,长、宽、高分别为4,3,6.若将它的表面沿某些棱剪开,展成一个平面图形,则下列图形中,可能是该长方体表面展开图的有 (填序号).
(2)图A,B分别是题(1)中长方体的两种表面展开图,求得图A的外围周长为52,请你求出图B的外围周长.
(3)第(1)题中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.
参考答案
一.选择题
1.解:第一个图是圆锥;第二个图是三棱锥;第三个图是正方体,也是四棱柱;第四个图是球;第五个图是圆柱;其中柱体有2个,即第三个和第五个,
故选:B.
2.解:根据正方体展开图可知“学”与“养”字所在面是相对面,
故选:D.
3.解:A、旋转一周为圆锥,故本选项错误;
B、旋转一周为圆锥,故本选项错误;
C、旋转一周能够得到图形的倒置图形,故本选项错误;
D、旋转一周能够得到如图图形,故本选项正确.
故选:D.
4.解:根据以上分析红色部分面积为9+4×(1+2+3)=33
故选:C.
5.解:根据有“田”字的展开图都不是正方体的表面展开图可知应剪去1或2或6,
故不应剪去的是3,
故选:B.
6.解:平面平行圆柱底面截圆柱可以得到一个圆,而倾斜截得到椭圆,故选:B.
7.解:圆柱的展开图是两个圆和一个矩形,
故选:D.
8.解:能同时堵住图中三个空洞的几何体是选项B的几何体.
故选:B.
9.解:甲所折成的无盖长方体的容积为:5×3×3=45(cm3),
乙所折成的无盖长方体的容积为:10×2×2=40(cm3),
丙所折成的无盖长方体的容积为:6×4×2=48(cm3),
∴丙>甲>乙.
故选:C.
10.解:∵大正方体的体积为125cm3,小正方体的体积为27cm3,
∴大正方体的棱长为5cm,小正方体的棱长为3cm,
∴大正方体的每个表面的面积为25cm2,小正方体的每个表面的面积为9cm2,
∴这个零件的表面积为:25×6+9×4=186(cm2),
答:要给这个零件的表面刷上油漆,则所需刷油漆的面积为186cm2.
故选:B.
二.填空题
11.解:由题意知,这种现象可以用数学原理解释为线动成面,
故答案为:线动成面.
12.解:设原长方体底面边长为a,长方体高为b,
则15=3a,2a+b=26,
解得a=5,b=16,
∴长方体的表面积为:5×5×2+5×16×4=370,
故答案为:370.
13.解:将图1的小正方形安放在图2中的②.③.④的其中某一个位置,经过折叠均能围成正方体,放在图2中的①位置,折叠后有两个面重叠,不能围成正方体,
故答案为:①.
14.解:由观察可知,
1周围四个面分别是4,5,2,3,
则1的对面是6;
又与3相邻的数是1,2,5,6,
则3的对面是4,则2与5相对,
所以?一定是1,6两个数中的一个,
又6同时和3、5相邻,则?处的数是6.
故答案为:6.
15.解:观察图象知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵2015÷4=503…3,
∴滚动第2014次后与第三次相同,
∴朝下的点数为5,
故答案为:5.
三.解答题
16.解:根据题意可知正方体的棱长是12÷3=4,
所以正方体的体积为43=64,
正方体的表面积为4×4×5=80.
答:这个无盖正方体的体积为64,表面积为80.
17.解:(1)以一组对边中点所在直线为轴旋转,能形成的几何体是圆柱体,说明的事实是面动成体,
故答案为:圆柱体,面动成体;
(2)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,
∴方案一构造的圆柱的体积大.
18.解:(1)根据几何体的展开图共有6个面,且各面有正方形及长方形,
∴此几何体为长方体,
故答案为:长方体;
(2)∵长方体有六个面,
∴用平面去截长方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴用一个平面去截长方体,截面的形状可能是三角形、四边形、五边形、六边形,
故答案为:①②③④;
(3)S=2×6×4+6×6×2=120cm2,V=6×6×2=72cm3,
答:表面积是120cm2,体积是72cm3.
19.解:由题意得:π×4××16=32π(m2).
2×π×22=8π(m2)
故至少需要塑料薄膜:32π+8π=40π(m)2
答:至少需要塑料薄膜40πm2.
20.解:(1)下列图形中,可能是该长方体表面展开图的有:①②③,
故答案为:①②③;
(2)图B的外围周长=4×6+4×4+6×3=58,
答:图B的外围周长是58;
(3)外围周长最大的表面展开图,如图所示:
由图可知:外围周长=8×6+4×4+3×2=70,
答:它的外围周长是70.
(附答案)
一.选择题
1.下列几何体中,属于柱体的有( )
A.1个 B.2个 C.3个 D.4个
2.将“数学核心素养”这几个字分别写在某个正方体的表面上,如图是它的一种展开图,将它折成正方体后,与“学”字所在面相对面上的汉字是( )
A.核 B.心 C.素 D.养
3.下列平面图形沿虚线旋转一周,可以得到如图所示的几何体的是( )
A. B. C. D.
4.把14个棱长为1的正方体在地面上堆叠如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为( )
A.21 B.24 C.33 D.37
5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则下列序号中不应剪去的是( )
A.6 B.3 C.2 D.1
6.如图所示,用一个平面去截一个圆柱,则截得的形状应为( )
A.B.C.D.
7.下列图形能折叠成圆柱的是( )
A. B.
C. D.
8.如图所示,下列几何体中能同时堵住图中三个空洞的几何体是( )
A. B. C. D.
9.在课题学习中,老师要求用长为12厘米,宽为8厘米的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分),然后沿虚线折成一个无盖的长方体纸盒.
甲:如图1,盒子底面的四边形ABCD是正方形;
乙:如图2,盒子底面的四边形ABCD是正方形;
丙:如图3,盒子底面的四边形ABCD是长方形,AB=2AD.
将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列,正确的是( )
A.甲>乙>丙 B.甲>丙>乙 C.丙>甲>乙 D.丙>乙>甲
10.如图的零件是由两个正方体焊接而成,已知大正方体和小正方体的体积分125cm3和27cm3,现要给这个零件的表面刷上油漆,那么所刷油漆的面积是( )cm2.
A.161 B.186 C.195 D.204
二.填空题
11.国扇文化有深厚的文化底蕴,历来中国有“制扇王国”之称.打开折扇时,随着扇骨的移动形成一个扇面,这种现象可以用数学原理解释为 .
12.如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,此长方体的表面积为 .
13.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是能围成一个正方体的.那么安放的位置不能是 .
14.一个立方体的每个面上都标有数字1、2、3、4、5、6,根据图中该立方体A、B、C三种状态所显示的数字,可推出“?”处的数字是
15.有一个正六面体骰子(如图)放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2015次后,骰子朝下一面的点数是 .
三.解答题
16.如图所示,边长为12的正方形纸板,四个角分别剪去一个相同的正方形,剩余部分折叠成无盖正方体,求这个无盖正方体的体积和表面积.
17.如图,有一个长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴旋转180°,可按两种方案进行操作.
方案一:以较长的一组对边中点所在直线为轴旋转,如图(1).
方案二:以较短的一组对边中点所在直线为轴旋转,如图(2).
(1)上述操作能形成的几何体是 ,说明的事实是 .
(2)请通过计算说明哪种方案得到的几何体的体积大.
18.如图是一个几何体的展开图.
(1)写出该几何体的名称 :
(2)用一个平面去截该几何体,截面形状可能是 (填序号);
①三角形;②四边形;③五边形;④六边形
(3)根据图中标注的长度(单位:cm),求该几何体的表面积和体积.
19.淘气家打算在一块长16m,宽4m的长方形菜地上搭建一个半圆柱形蔬菜棚,并全部盖上塑料薄膜(如图),这个蔬菜棚至少要用多少平方米的塑料薄膜?
20.(1)如图所示的长方体,长、宽、高分别为4,3,6.若将它的表面沿某些棱剪开,展成一个平面图形,则下列图形中,可能是该长方体表面展开图的有 (填序号).
(2)图A,B分别是题(1)中长方体的两种表面展开图,求得图A的外围周长为52,请你求出图B的外围周长.
(3)第(1)题中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.
参考答案
一.选择题
1.解:第一个图是圆锥;第二个图是三棱锥;第三个图是正方体,也是四棱柱;第四个图是球;第五个图是圆柱;其中柱体有2个,即第三个和第五个,
故选:B.
2.解:根据正方体展开图可知“学”与“养”字所在面是相对面,
故选:D.
3.解:A、旋转一周为圆锥,故本选项错误;
B、旋转一周为圆锥,故本选项错误;
C、旋转一周能够得到图形的倒置图形,故本选项错误;
D、旋转一周能够得到如图图形,故本选项正确.
故选:D.
4.解:根据以上分析红色部分面积为9+4×(1+2+3)=33
故选:C.
5.解:根据有“田”字的展开图都不是正方体的表面展开图可知应剪去1或2或6,
故不应剪去的是3,
故选:B.
6.解:平面平行圆柱底面截圆柱可以得到一个圆,而倾斜截得到椭圆,故选:B.
7.解:圆柱的展开图是两个圆和一个矩形,
故选:D.
8.解:能同时堵住图中三个空洞的几何体是选项B的几何体.
故选:B.
9.解:甲所折成的无盖长方体的容积为:5×3×3=45(cm3),
乙所折成的无盖长方体的容积为:10×2×2=40(cm3),
丙所折成的无盖长方体的容积为:6×4×2=48(cm3),
∴丙>甲>乙.
故选:C.
10.解:∵大正方体的体积为125cm3,小正方体的体积为27cm3,
∴大正方体的棱长为5cm,小正方体的棱长为3cm,
∴大正方体的每个表面的面积为25cm2,小正方体的每个表面的面积为9cm2,
∴这个零件的表面积为:25×6+9×4=186(cm2),
答:要给这个零件的表面刷上油漆,则所需刷油漆的面积为186cm2.
故选:B.
二.填空题
11.解:由题意知,这种现象可以用数学原理解释为线动成面,
故答案为:线动成面.
12.解:设原长方体底面边长为a,长方体高为b,
则15=3a,2a+b=26,
解得a=5,b=16,
∴长方体的表面积为:5×5×2+5×16×4=370,
故答案为:370.
13.解:将图1的小正方形安放在图2中的②.③.④的其中某一个位置,经过折叠均能围成正方体,放在图2中的①位置,折叠后有两个面重叠,不能围成正方体,
故答案为:①.
14.解:由观察可知,
1周围四个面分别是4,5,2,3,
则1的对面是6;
又与3相邻的数是1,2,5,6,
则3的对面是4,则2与5相对,
所以?一定是1,6两个数中的一个,
又6同时和3、5相邻,则?处的数是6.
故答案为:6.
15.解:观察图象知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵2015÷4=503…3,
∴滚动第2014次后与第三次相同,
∴朝下的点数为5,
故答案为:5.
三.解答题
16.解:根据题意可知正方体的棱长是12÷3=4,
所以正方体的体积为43=64,
正方体的表面积为4×4×5=80.
答:这个无盖正方体的体积为64,表面积为80.
17.解:(1)以一组对边中点所在直线为轴旋转,能形成的几何体是圆柱体,说明的事实是面动成体,
故答案为:圆柱体,面动成体;
(2)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,
∴方案一构造的圆柱的体积大.
18.解:(1)根据几何体的展开图共有6个面,且各面有正方形及长方形,
∴此几何体为长方体,
故答案为:长方体;
(2)∵长方体有六个面,
∴用平面去截长方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴用一个平面去截长方体,截面的形状可能是三角形、四边形、五边形、六边形,
故答案为:①②③④;
(3)S=2×6×4+6×6×2=120cm2,V=6×6×2=72cm3,
答:表面积是120cm2,体积是72cm3.
19.解:由题意得:π×4××16=32π(m2).
2×π×22=8π(m2)
故至少需要塑料薄膜:32π+8π=40π(m)2
答:至少需要塑料薄膜40πm2.
20.解:(1)下列图形中,可能是该长方体表面展开图的有:①②③,
故答案为:①②③;
(2)图B的外围周长=4×6+4×4+6×3=58,
答:图B的外围周长是58;
(3)外围周长最大的表面展开图,如图所示:
由图可知:外围周长=8×6+4×4+3×2=70,
答:它的外围周长是70.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
