22.3 实际问题与二次函数 同步练习 2023—2024学年人教版数学九年级上册(无答案)
文档属性
| 名称 | 22.3 实际问题与二次函数 同步练习 2023—2024学年人教版数学九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 524.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 20:34:20 | ||
图片预览

文档简介
22.3 实际问题与二次函数 同步精练
一、单选题
1.向阳村2020年的人均年收入为12000元,2022年的人均年收入为14520元.设人均年收入的平均增长率为x,则下列所列的方程中正确的是( )
A. B.
C. D.
2.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
3.如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( ).
A.12 B.18 C.20 D.24
4.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.m D.m
5.利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B., C., D.,
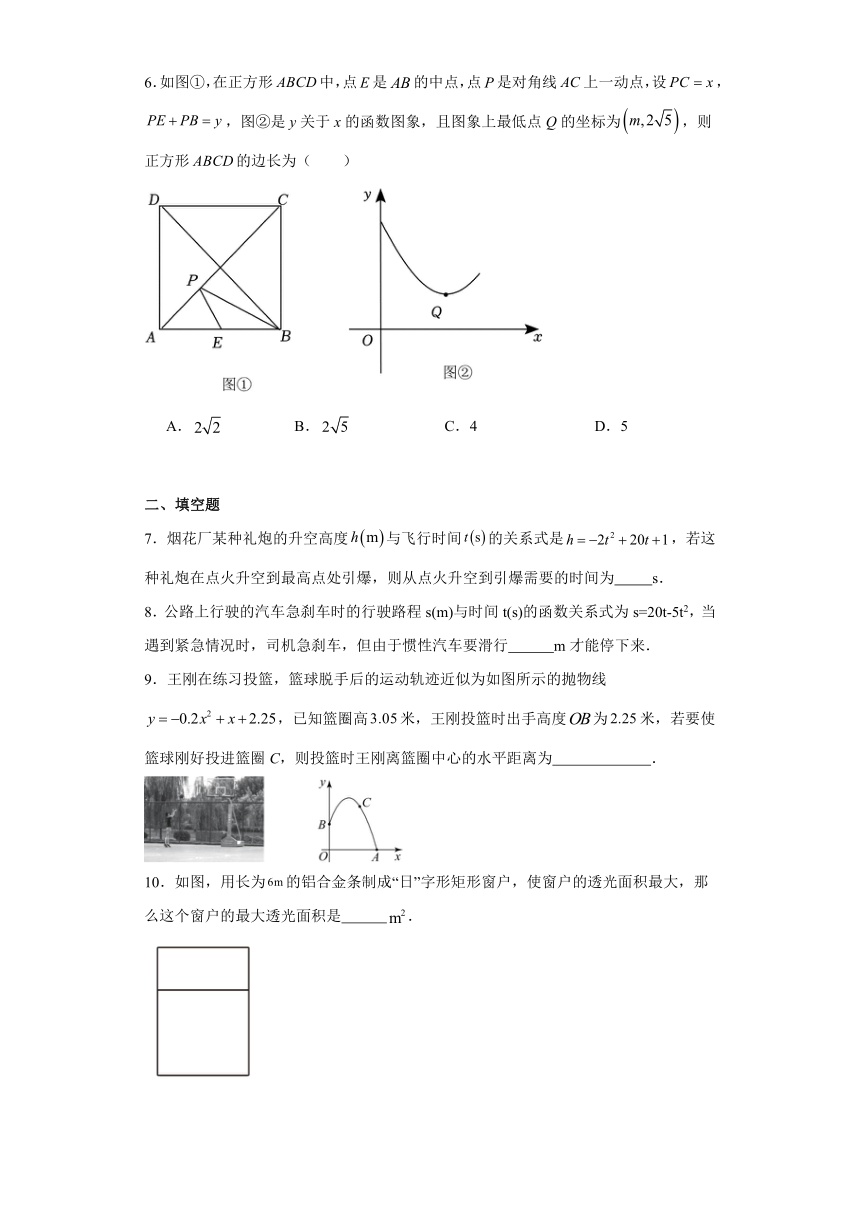
6.如图①,在正方形中,点E是的中点,点P是对角线上一动点,设,,图②是y关于x的函数图象,且图象上最低点Q的坐标为,则正方形的边长为( )
A. B. C.4 D.5
二、填空题
7.烟花厂某种礼炮的升空高度与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为 s.
8.公路上行驶的汽车急刹车时的行驶路程s(m)与时间t(s)的函数关系式为s=20t-5t2,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 m才能停下来.
9.王刚在练习投篮,篮球脱手后的运动轨迹近似为如图所示的抛物线,已知篮圈高米,王刚投篮时出手高度为米,若要使篮球刚好投进篮圈C,则投篮时王刚离篮圈中心的水平距离为 .
10.如图,用长为的铝合金条制成“日”字形矩形窗户,使窗户的透光面积最大,那么这个窗户的最大透光面积是 .
11.如图,矩形的两边长,,点M、N分别从A、B同时出发.M在边上沿方向以每秒的速度匀速运动,N在边上沿方向以每秒的速度的匀速运动,当N到达C点时,M、N停止运动.当运动时间 秒时,的面积最大,最大值为 .
12.如图,在斜坡底部点O处设置一个可移动的自动喷水装置,喷水装置的高度为米,喷水装置从A点喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为6米时,达到最大高度5米.以点O为原点,喷水装置所在的直线为y轴,建立平面直角坐标系.斜坡上距离O水平距离为8米处有一棵高度为米的小树,垂直水平地面且M点到水平地面的距离为米.如果要使水流恰好喷射到小树顶端的点N,请求出自动喷水装置应向后平移(即抛物线向左平移) 米.
三、解答题
13.如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园(矩形),墙长为,这个矩形的长,菜园的面积为,且.
(1)求与之问的函数关系式,并写出自变量的取值范围.
(2)当该菜园的长为多少时,菜园的面积最大?最大面积是多少?
14.一个物体从地面竖直向上抛,有这样的关系式:(不计空气阻力),其中是物体距离地面的高度,是初速度,是重力加速度(g取),t是抛出后所经历的时间.圆圆用发射器(发射器的高度忽略不计)将一个小球以的初速度从地面竖直向上抛.
(1)当小球的高度为米时,求时间的值;
(2)小球的高度能达到米吗?请作出判断,并说明理由.
15.一座拱桥的界面轮廓为抛物线型(如图1),拱高,跨度.
(1)将抛物线放在所给的直角坐标系中(如图2),其表达式是的形式,请根据所给的数据求出该抛物线表达式.
(2)拱桥下地平面是双向行车道(正中间隔离带宽度不计),其中的一条行车道要能并排行驶三辆宽的汽车(汽车间的间隔忽略不计),则在最外侧车道上的汽车最高为多少米?
16.党的二十大已经胜利闭幕,各行各业的人们用拼搏奋斗凝聚起奋进新征程、建功新时代的磅礴力量,信心满怀向未来.某商店决定对某类商品进行降价促销活动:已知进价为每件元,平时以单价元的价格售出一天可卖件.根据调查单价每降低元,每天可多售出件;设商品售价元(售价不低于进价,为正整数),这批商品的日利润为元(),请解决以下问题:
(1)当商品的售价为多少元时,销售这批商品的日利润最大,最大值为多少?
(2)若商店每卖一件就捐元()给希望小学,该店发现售价为元时可获得最大日利润,求的取值范围.
17.2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为4米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为,着陆坡顶端与落地点的距离为米,.求:
(1)点的坐标;
(2)该抛物线的函数表达式;
(3)起跳点与着陆坡顶端之间的水平距离的长.
18.在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处,小聪测量黑球减速后的运动速度(单位:cm/s)、运动距离(单位:cm)随运动时间t(单位:s)变化的数据,整理得下表.小聪探究发现,黑球的运动速度v与运动时间t之间成一次函数关系,运动距离y与运动时间t之间成二次函数关系.
运动时间t(s) 0 4 8 12 …
运动速度v(cm/s) 10 8 6 4 …
运动距离y(cm) 0 36 64 84 …
(1)直接写出v关于t的函数表达式和y关于t的函数表达式;(不要求写出自变量的取值范围)
(2)当黑球减速后运动距离为时,求它此时的运动速度;
(3)若白球一直以3cm/s的速度匀速运动,问黑球在运动过程中会不会触到白球?若不能,请求出两球之间距离的最小值;若能,请求出运动时间t.
一、单选题
1.向阳村2020年的人均年收入为12000元,2022年的人均年收入为14520元.设人均年收入的平均增长率为x,则下列所列的方程中正确的是( )
A. B.
C. D.
2.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0).若此炮弹在第6秒与第18秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
3.如图,四边形ABCD的两条对角线互相垂直,AC+BD=12,则四边形ABCD的面积最大值是( ).
A.12 B.18 C.20 D.24
4.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m B.4m C.m D.m
5.利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B., C., D.,
6.如图①,在正方形中,点E是的中点,点P是对角线上一动点,设,,图②是y关于x的函数图象,且图象上最低点Q的坐标为,则正方形的边长为( )
A. B. C.4 D.5
二、填空题
7.烟花厂某种礼炮的升空高度与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为 s.
8.公路上行驶的汽车急刹车时的行驶路程s(m)与时间t(s)的函数关系式为s=20t-5t2,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 m才能停下来.
9.王刚在练习投篮,篮球脱手后的运动轨迹近似为如图所示的抛物线,已知篮圈高米,王刚投篮时出手高度为米,若要使篮球刚好投进篮圈C,则投篮时王刚离篮圈中心的水平距离为 .
10.如图,用长为的铝合金条制成“日”字形矩形窗户,使窗户的透光面积最大,那么这个窗户的最大透光面积是 .
11.如图,矩形的两边长,,点M、N分别从A、B同时出发.M在边上沿方向以每秒的速度匀速运动,N在边上沿方向以每秒的速度的匀速运动,当N到达C点时,M、N停止运动.当运动时间 秒时,的面积最大,最大值为 .
12.如图,在斜坡底部点O处设置一个可移动的自动喷水装置,喷水装置的高度为米,喷水装置从A点喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为6米时,达到最大高度5米.以点O为原点,喷水装置所在的直线为y轴,建立平面直角坐标系.斜坡上距离O水平距离为8米处有一棵高度为米的小树,垂直水平地面且M点到水平地面的距离为米.如果要使水流恰好喷射到小树顶端的点N,请求出自动喷水装置应向后平移(即抛物线向左平移) 米.
三、解答题
13.如图,用一段长为的篱笆围成一个一边靠墙的矩形菜园(矩形),墙长为,这个矩形的长,菜园的面积为,且.
(1)求与之问的函数关系式,并写出自变量的取值范围.
(2)当该菜园的长为多少时,菜园的面积最大?最大面积是多少?
14.一个物体从地面竖直向上抛,有这样的关系式:(不计空气阻力),其中是物体距离地面的高度,是初速度,是重力加速度(g取),t是抛出后所经历的时间.圆圆用发射器(发射器的高度忽略不计)将一个小球以的初速度从地面竖直向上抛.
(1)当小球的高度为米时,求时间的值;
(2)小球的高度能达到米吗?请作出判断,并说明理由.
15.一座拱桥的界面轮廓为抛物线型(如图1),拱高,跨度.
(1)将抛物线放在所给的直角坐标系中(如图2),其表达式是的形式,请根据所给的数据求出该抛物线表达式.
(2)拱桥下地平面是双向行车道(正中间隔离带宽度不计),其中的一条行车道要能并排行驶三辆宽的汽车(汽车间的间隔忽略不计),则在最外侧车道上的汽车最高为多少米?
16.党的二十大已经胜利闭幕,各行各业的人们用拼搏奋斗凝聚起奋进新征程、建功新时代的磅礴力量,信心满怀向未来.某商店决定对某类商品进行降价促销活动:已知进价为每件元,平时以单价元的价格售出一天可卖件.根据调查单价每降低元,每天可多售出件;设商品售价元(售价不低于进价,为正整数),这批商品的日利润为元(),请解决以下问题:
(1)当商品的售价为多少元时,销售这批商品的日利润最大,最大值为多少?
(2)若商店每卖一件就捐元()给希望小学,该店发现售价为元时可获得最大日利润,求的取值范围.
17.2022北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为4米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为,着陆坡顶端与落地点的距离为米,.求:
(1)点的坐标;
(2)该抛物线的函数表达式;
(3)起跳点与着陆坡顶端之间的水平距离的长.
18.在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处,小聪测量黑球减速后的运动速度(单位:cm/s)、运动距离(单位:cm)随运动时间t(单位:s)变化的数据,整理得下表.小聪探究发现,黑球的运动速度v与运动时间t之间成一次函数关系,运动距离y与运动时间t之间成二次函数关系.
运动时间t(s) 0 4 8 12 …
运动速度v(cm/s) 10 8 6 4 …
运动距离y(cm) 0 36 64 84 …
(1)直接写出v关于t的函数表达式和y关于t的函数表达式;(不要求写出自变量的取值范围)
(2)当黑球减速后运动距离为时,求它此时的运动速度;
(3)若白球一直以3cm/s的速度匀速运动,问黑球在运动过程中会不会触到白球?若不能,请求出两球之间距离的最小值;若能,请求出运动时间t.
同课章节目录
