3.3勾股定理的应用举例(第二课时) 导学案 (无答案)2023—2024学年鲁教版(五四制)数学七年级上册
文档属性
| 名称 | 3.3勾股定理的应用举例(第二课时) 导学案 (无答案)2023—2024学年鲁教版(五四制)数学七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1023.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 21:55:34 | ||
图片预览

文档简介
3.3勾股定理的应用举例(第二课时)学案
学习目标:
熟练运用勾股定理及逆定理解决实际问题,学会把实际问题转化为数学问题;
利用勾股定理解决古代问题,体会传统文化的魅力。
学习重、难点:
把实际问题转化为数学问题,建立数学模型,形成解题思路;
能正确画出古代问题的几何图形,学会对应已知关系。
复习与回顾:
说出勾股定理及逆定理,并举例说明应用;
应用练习:
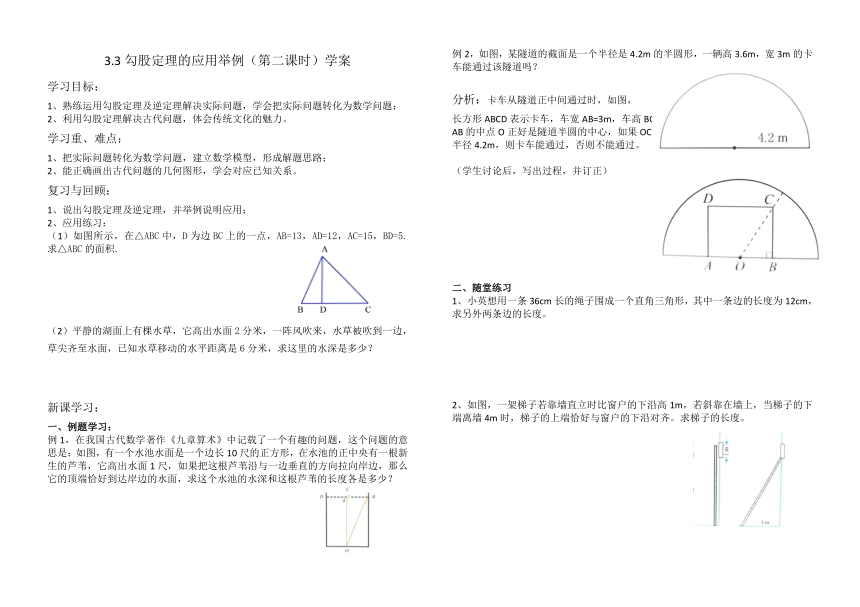
(1)如图所示,在△ABC中,D为边BC上的一点,AB=13,AD=12,AC=15,BD=5.求△ABC的面积.
(2)平静的湖面上有棵水草,它高出水面2分米,一阵风吹来,水草被吹到一边,草尖齐至水面,已知水草移动的水平距离是6分米,求这里的水深是多少?
新课学习:
例题学习:
例1,在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池水面是一个边长10尺的正方形,在水池的正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,那么它的顶端恰好到达岸边的水面,求这个水池的水深和这根芦苇的长度各是多少?
例2,如图,某隧道的截面是一个半径是4.2m的半圆形,一辆高3.6m,宽3m的卡车能通过该隧道吗?
分析:卡车从隧道正中间通过时,如图,
长方形ABCD表示卡车,车宽AB=3m,车高BC=3.6m
AB的中点O正好是隧道半圆的中心,如果OC的长小于
半径4.2m,则卡车能通过,否则不能通过。
(学生讨论后,写出过程,并订正)
随堂练习
小英想用一条36cm长的绳子围成一个直角三角形,其中一条边的长度为12cm,
求另外两条边的长度。
2、如图,一架梯子若靠墙直立时比窗户的下沿高1m,若斜靠在墙上,当梯子的下端离墙4m时,梯子的上端恰好与窗户的下沿对齐。求梯子的长度。
3、如图,在四边形ABCD中,∠A=90°,AB=4cm,AD=2cm,BC=CD,E是AB上的一点,若沿CE折叠,则B、D两点重合,求△AED的面积。
课堂小结:
学会把实际问题转化为数学问题的方法;
能建立数学模型,解决问题。
集中练习:
1.若等腰三角形腰长为10cm,底边长为16 cm,那么它的面积为 ( )
A.48 cm2 B.36 cm2 C.24 cm2 D.12 cm2
2.若△ABC中,AB=13,AC=15,高AD=12,则BC的长是( )
A.14 B.4 C.14或4 D.以上都不对
3.已知:如图,在Rt△ABC中,两直角边AC、BC的长分别为6和8,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.2 B.3 C.4 D.5
4.如图,一场大风后,一棵与地面垂直的树在离地面1.5m处的A点折断,树尖B点触地,经测量BC=2m,那么树高是 .
5.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,则离开港口2小时后,两船相距多少海里?
6.如图,在长方形ABCD中,将ABC沿AC对折至AEC位置,CE与AD交于点F。
(1)试说明:AF=FC;(2)如果AB=3,BC=4,求AF的长
当堂检测
1. 若等腰三角形腰长为10cm,底边长为16 cm,那么它的面积为 ( )
A.48 cm2 B.36 cm2 C.24 cm2 D.12 cm2
2. 若△ABC中,AB=13,AC=15,高AD=12,则BC的长是( )
A.14 B.4 C.14或4 D.以上都不对
3.已知:如图①,在Rt△ABC中,两直角边AC、BC的长分别为6和8,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.2 B.3 C.4 D.5
4.下列说法不能推出△ABC是直角三角形的是( )
A.a2-c2=b2 B.(a-b)(a+b)+c2=0
C.∠A=∠B=∠C D.∠A=2∠B=2∠C
5.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,则离开港口2小时后,两船相距多少海
6.一种盛饮料的圆柱形杯(如图),测得内部地面半径为2.5cm,高为12cm,吸管斜置于杯中,并在杯口外面至少露出4.6cm,问吸管需要多长?
学习目标:
熟练运用勾股定理及逆定理解决实际问题,学会把实际问题转化为数学问题;
利用勾股定理解决古代问题,体会传统文化的魅力。
学习重、难点:
把实际问题转化为数学问题,建立数学模型,形成解题思路;
能正确画出古代问题的几何图形,学会对应已知关系。
复习与回顾:
说出勾股定理及逆定理,并举例说明应用;
应用练习:
(1)如图所示,在△ABC中,D为边BC上的一点,AB=13,AD=12,AC=15,BD=5.求△ABC的面积.
(2)平静的湖面上有棵水草,它高出水面2分米,一阵风吹来,水草被吹到一边,草尖齐至水面,已知水草移动的水平距离是6分米,求这里的水深是多少?
新课学习:
例题学习:
例1,在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池水面是一个边长10尺的正方形,在水池的正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,那么它的顶端恰好到达岸边的水面,求这个水池的水深和这根芦苇的长度各是多少?
例2,如图,某隧道的截面是一个半径是4.2m的半圆形,一辆高3.6m,宽3m的卡车能通过该隧道吗?
分析:卡车从隧道正中间通过时,如图,
长方形ABCD表示卡车,车宽AB=3m,车高BC=3.6m
AB的中点O正好是隧道半圆的中心,如果OC的长小于
半径4.2m,则卡车能通过,否则不能通过。
(学生讨论后,写出过程,并订正)
随堂练习
小英想用一条36cm长的绳子围成一个直角三角形,其中一条边的长度为12cm,
求另外两条边的长度。
2、如图,一架梯子若靠墙直立时比窗户的下沿高1m,若斜靠在墙上,当梯子的下端离墙4m时,梯子的上端恰好与窗户的下沿对齐。求梯子的长度。
3、如图,在四边形ABCD中,∠A=90°,AB=4cm,AD=2cm,BC=CD,E是AB上的一点,若沿CE折叠,则B、D两点重合,求△AED的面积。
课堂小结:
学会把实际问题转化为数学问题的方法;
能建立数学模型,解决问题。
集中练习:
1.若等腰三角形腰长为10cm,底边长为16 cm,那么它的面积为 ( )
A.48 cm2 B.36 cm2 C.24 cm2 D.12 cm2
2.若△ABC中,AB=13,AC=15,高AD=12,则BC的长是( )
A.14 B.4 C.14或4 D.以上都不对
3.已知:如图,在Rt△ABC中,两直角边AC、BC的长分别为6和8,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.2 B.3 C.4 D.5
4.如图,一场大风后,一棵与地面垂直的树在离地面1.5m处的A点折断,树尖B点触地,经测量BC=2m,那么树高是 .
5.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,则离开港口2小时后,两船相距多少海里?
6.如图,在长方形ABCD中,将ABC沿AC对折至AEC位置,CE与AD交于点F。
(1)试说明:AF=FC;(2)如果AB=3,BC=4,求AF的长
当堂检测
1. 若等腰三角形腰长为10cm,底边长为16 cm,那么它的面积为 ( )
A.48 cm2 B.36 cm2 C.24 cm2 D.12 cm2
2. 若△ABC中,AB=13,AC=15,高AD=12,则BC的长是( )
A.14 B.4 C.14或4 D.以上都不对
3.已知:如图①,在Rt△ABC中,两直角边AC、BC的长分别为6和8,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A.2 B.3 C.4 D.5
4.下列说法不能推出△ABC是直角三角形的是( )
A.a2-c2=b2 B.(a-b)(a+b)+c2=0
C.∠A=∠B=∠C D.∠A=2∠B=2∠C
5.如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,则离开港口2小时后,两船相距多少海
6.一种盛饮料的圆柱形杯(如图),测得内部地面半径为2.5cm,高为12cm,吸管斜置于杯中,并在杯口外面至少露出4.6cm,问吸管需要多长?
