2.5等腰三角形的轴对称性 解答题专题训练 (含答案)2023-2024学年苏科版八年级数学上册
文档属性
| 名称 | 2.5等腰三角形的轴对称性 解答题专题训练 (含答案)2023-2024学年苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 22:06:47 | ||
图片预览


文档简介
2023-2024学年苏科版八年级数学上册《2.5等腰三角形的轴对称性》
解答题专题训练(附答案)
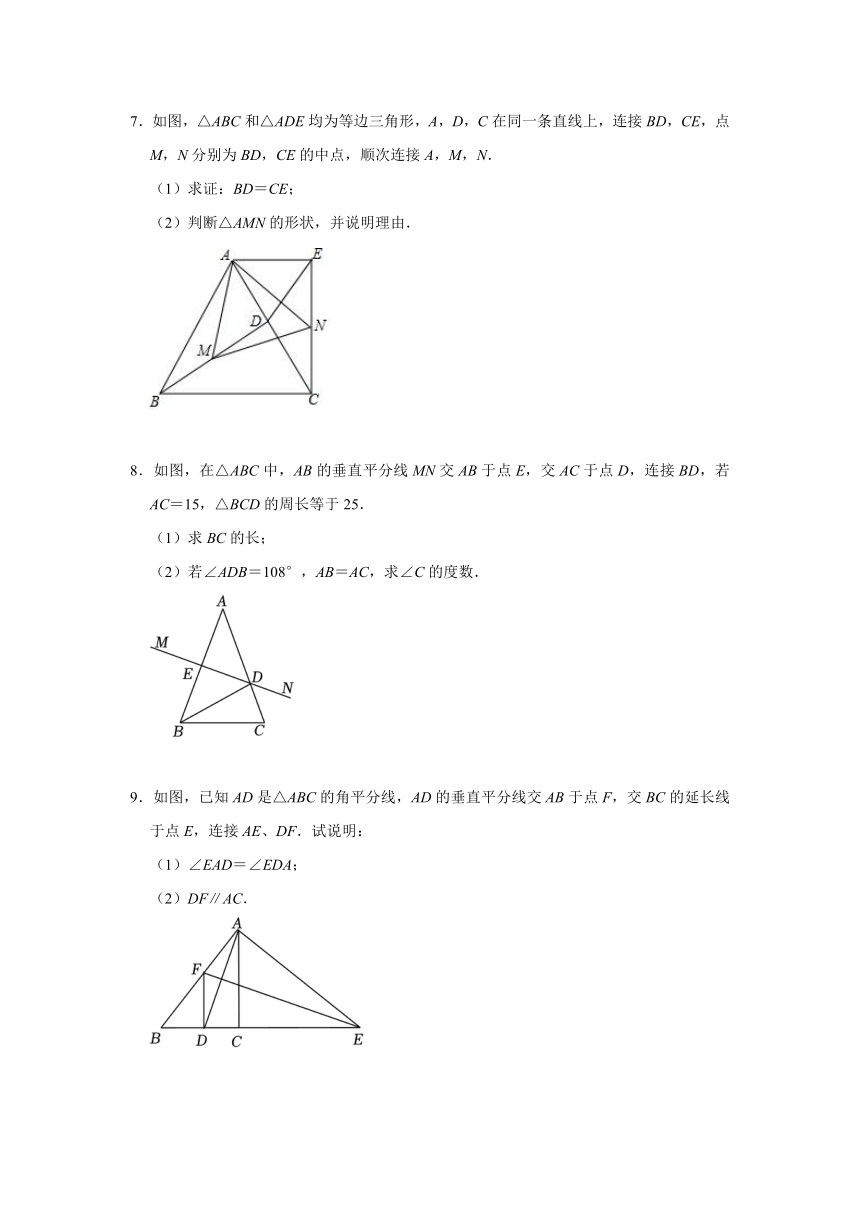
1.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接AF.
(1)求证:DF=BF;
(2)连接CE,求证直线AF是线段CE的垂直平分线.
2.如图,点B、F、C、E在一条直线上,△ABC≌△DEF,连结AD交BE于O.
(1)求证:AC∥FD,AB∥ED;
(2)求证:AO=DO.
3.如图,已知,△ABC≌△ADE,AD与BC交于点F,点C在DE上,∠B=30°,∠AFC=70°.
(1)求∠FCD的度数;
(2)求证:AC=AF.
4.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当α为多少度时,△AOD是等腰三角形,请说明理由.
5.如图,在等边△ABC中,点D为边BC上一点,∠ABE=∠CAD,CF∥BE交AD的延长线于点F.
(1)求∠AEB的度数;
(2)若BE=10,AF=15,求AE的长.
6.如图,在△ABC中,AC>BC,∠A=45°,点D是AB边上一点,且CD=CB,过点B作BF⊥CD于点E,与AC交于点F点,画出∠DCB的角平分线交AB于G并回答以下问题:
(1)求证:∠ABF=∠BCD;
(2)判断△BCF的形状,并说明理由.
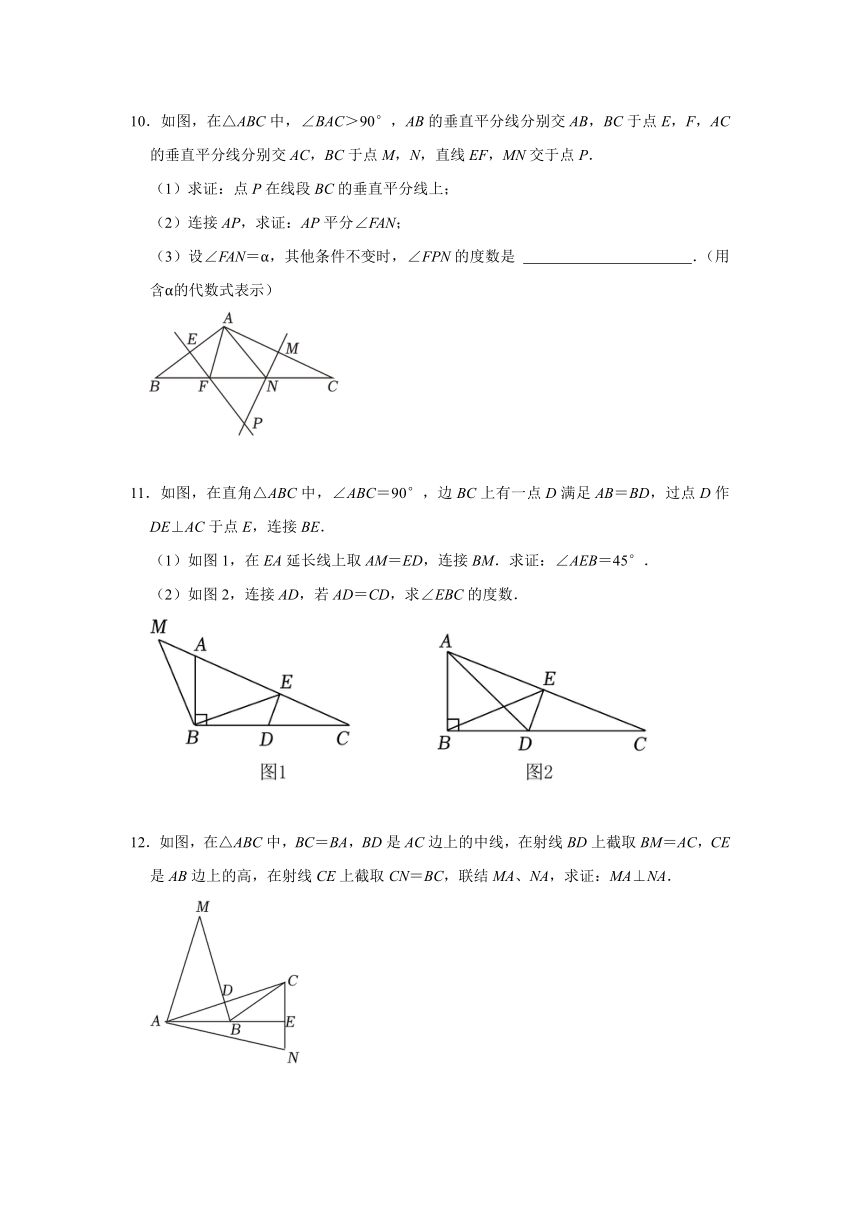
7.如图,△ABC和△ADE均为等边三角形,A,D,C在同一条直线上,连接BD,CE,点M,N分别为BD,CE的中点,顺次连接A,M,N.
(1)求证:BD=CE;
(2)判断△AMN的形状,并说明理由.
8.如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,连接BD,若AC=15,△BCD的周长等于25.
(1)求BC的长;
(2)若∠ADB=108°,AB=AC,求∠C的度数.
9.如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
(1)∠EAD=∠EDA;
(2)DF∥AC.
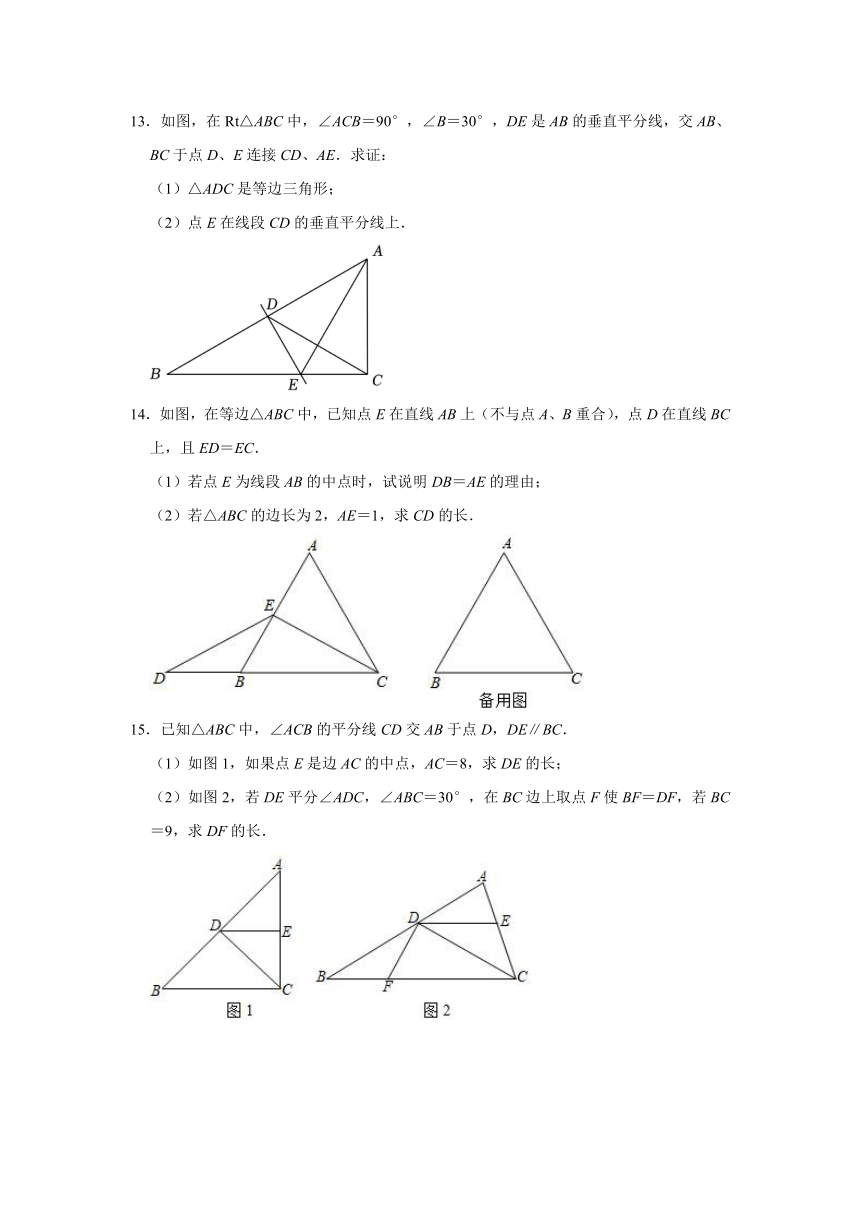
10.如图,在△ABC中,∠BAC>90°,AB的垂直平分线分别交AB,BC于点E,F,AC的垂直平分线分别交AC,BC于点M,N,直线EF,MN交于点P.
(1)求证:点P在线段BC的垂直平分线上;
(2)连接AP,求证:AP平分∠FAN;
(3)设∠FAN=α,其他条件不变时,∠FPN的度数是 .(用含α的代数式表示)
11.如图,在直角△ABC中,∠ABC=90°,边BC上有一点D满足AB=BD,过点D作DE⊥AC于点E,连接BE.
(1)如图1,在EA延长线上取AM=ED,连接BM.求证:∠AEB=45°.
(2)如图2,连接AD,若AD=CD,求∠EBC的度数.
12.如图,在△ABC中,BC=BA,BD是AC边上的中线,在射线BD上截取BM=AC,CE是AB边上的高,在射线CE上截取CN=BC,联结MA、NA,求证:MA⊥NA.
13.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,DE是AB的垂直平分线,交AB、BC于点D、E连接CD、AE.求证:
(1)△ADC是等边三角形;
(2)点E在线段CD的垂直平分线上.
14.如图,在等边△ABC中,已知点E在直线AB上(不与点A、B重合),点D在直线BC上,且ED=EC.
(1)若点E为线段AB的中点时,试说明DB=AE的理由;
(2)若△ABC的边长为2,AE=1,求CD的长.
15.已知△ABC中,∠ACB的平分线CD交AB于点D,DE∥BC.
(1)如图1,如果点E是边AC的中点,AC=8,求DE的长;
(2)如图2,若DE平分∠ADC,∠ABC=30°,在BC边上取点F使BF=DF,若BC=9,求DF的长.
16.如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线交于点D,DG⊥AB,DH⊥AC,G,H为垂足.
(1)求证:BG=CH;
(2)若AB=8,AC=6,求AG的长.
17.如图,BM平分∠ABC,D为AC的中点,且MD⊥AC,过点M作ME⊥BC于点E,MF⊥AB于点F.
(1)求证:AF=CE;
(2)如果BC=8,AB=4,求BE,AF的长.
18.在△ABC中,AB=AC,∠BAC=90°,点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰直角三角形ADE,使∠DAE=90°,AD=AE.
(1)当点D在线段BC上时,如图①,求证:①BC=CE+CD;②CE⊥BC.
(2)当点D在线段CB的延长线上时,如图②,(1)中的两个结论是否仍然成立.若成立,请给予证明;若不成立,请说明理由.
19.如图,在△ABC中,∠B=90°,AB=3,BC=4.点P从点B出发,沿BC边以每秒1个单位长度的速度运动,到达点C后立即以每秒2个单位长度的速度返回点B,点P运动的时间为t秒.
(1)点P返回点B时,共耗时 秒;
(2)当t=5时,求BP的长;
(3)当点P到达点C之前,求△ACP的面积(用含t的代数式表示);
(4)当△ABP是等腰三角形时,直接写出t的值.
20.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.
(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,只探究BD与CE之间的关系.(只写结论,不必说明理由)
参考答案
1.证明:(1)∵Rt△ABC≌Rt△ADE,
∴AB=AD,
在Rt△ADF与Rt△ABF中,
,
∴Rt△ADF≌Rt△ABF(HL),
∴DF=BF;
(2)连接CE,∵Rt△ABC≌Rt△ADE,
∴BC=DE,AC=AE,
∵DF=BF,
∴FC=FE,
∴点A和点F在CE的中垂线上,
∴AF是CE的中垂线.
2.(1)证明:∵△ABC≌△DEF,
∴∠B=∠E,∠ACB=∠EFD,
∴AB∥DE,AC∥DF;
(2)证明:∵△ABC≌△DEF,
∴∠ACB=∠EFD,AC=DF,
在△ACO和△DFO中,
,
∴△ACO≌△DFO(AAS),
∴AO=DO.
3.(1)解:∵△ABC≌△ADE,
∴∠B=∠D=30°,
∵∠AFC=70°,
∴∠FCD=∠AFC﹣∠D=70°﹣30°=40°;
(2)证明:∵△ABC≌△ADE,
∴AE=AC,∠E=∠ACB,
∴∠E=∠ACE=∠ACB,
由(1)知,∠FCD=40°,
∴∠ACF=(180°﹣∠FCD)=(180°﹣40°)=70°,
∵∠AFC=70°,
∴∠ACF=∠AFC,
∴AC=AF.
4.解:(1)△AOD是直角三角形,理由如下:
∵△BOC≌△ADC,∠α=150°,
∴OC=DC,∠ADC=∠BOC=∠α=150°,
∵∠OCD=60°,
∴△OCD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形;
(2)当α=110°或125°或140°时,△AOD是等腰三角形,理由如下:
∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
5.解:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∵∠ABE=∠CAD,
∴∠CAD+∠BAE=∠ABE+∠BAE=∠BAC=60°,
∴∠AEB=120°;
(2)如图,在AF上截取FH=FC,连接CH,
∵∠AEB=120°,
∴∠BED=60°,
∵BE∥CF,
∴∠BED=∠F=60°,
又∵FH=FC,
∴△FCH是等边三角形,
∴CF=CH=FH,∠FCH=∠FHC=60°,
∴∠AHC=120°=∠AEB,
在△ABE和△CAH中,
,
∴△ABE≌△CAH(AAS),
∴BE=AH=10,AE=CH,
∴FH=CH=AE=5.
6.(1)证明:过点C作CG⊥AB于点G,
∴∠DCG+∠CDG=90°,
∵BC=DC,
∴∠BCG=∠DCG=∠BCD,
∵BF⊥CD于点E,
∴∠ABF+∠CDG=90°,
∴∠ABF=∠DCG=∠BCD;
(2)解:△BCF是等腰三角形,
理由:如图,∵∠A=45°,CG⊥AB,
∴∠ACG=45°,
∵∠ACB=∠ACG+∠BCG,∠BFC=∠A+∠ABF,
∴∠ACB=45°+∠BCG,∠BFC=45°+∠ABF,
∵∠BCG=∠DCG=∠ABF,
∴∠BCF=∠BFC,
∴BC=BF,
∴△BCF是等腰三角形.
7.证明:(1)∵△ABC和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)△AMN是等边三角形,
理由如下:
∵点M,N分别为BD,CE的中点,BD=CE,
∴BM=CN,
∵△ABD≌△ACE,
∴∠ABM=∠ACN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴AM=AN,∠BAM=∠CAN,
∴∠MAN=∠BAC﹣∠BAM+∠CAN=60°,
∴△AMN是等边三角形.
8.解:(1)∵MN是AB的垂直平分线,
∴AD=BD,
∵AC=15,△BCD的周长等于25,
∴BC+CD+BD=BC+CD+AD=BC+AC=25,
∴BC=10.
(2)∵MN是AB的垂直平分线,∠ADB=108°,
∴,∠AED=90°.
∴∠A=36°,
∵AB=AC,
∴.
9.证明:(1)∵EF是AD的垂直平分线,
∴EA=ED,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴FA=FD,
∴∠FDA=∠FAD,
∵AD平分∠BAC,
∴∠FAD=∠CAD,
∴∠FDA=∠CAD,
∴DF∥AC.
10.(1)证明:如图,连接PA,PB,PC.
∵PE垂直平分AB,PM垂直平分AC,
∴PA=PB,PA=PC,
∴PB=PC,
∴点P在线段BC的垂直平分线上.
(2)证明:由(1)知PB=PC,
∴∠PBF=∠PCN,
∵PE垂直平分AB,
∴PA=PB,FA=FB,
∴∠PAB=∠PBA,∠FAB=∠FBA,
∴∠PAF=∠PBF,
同理∠PAN=∠PCN,
∴∠PAF=∠PAN,即AP平分∠FAN.
(3)解:∵PE垂直平分AB,PM垂直平分AC,
∴FA=FB,NA=NC,∠AEP=∠AMP=90°,
设∠B=x,∠C=y,
∴∠B=x=∠BAF,∠C=y=∠CAN,
在△ABC中,∠B+∠C+∠CAB=180°,∠FAN=α,
∴x+y+x+y+α=180°,即,
在四边形AEPM中,∠AEP+∠AMP+∠EAM+∠FPN=360°,
∴,
故答案为:.
11.(1)证明:∵DE⊥AC,
∴∠DEC=90°=∠ABC,
∴∠DEC+∠C=∠ABC+∠C,即∠BDE=∠MAB,
∵AB=BD,AM=DE,
∴△MAB≌△EDB(SAS),
∴∠MBA=∠EBD,BM=BE,
∴∠MBA+∠ABE=∠EBD+∠ABE=∠ABC=90°,即∠MBE=90°,
∴△MBE是等腰直角三角形,
∴∠AEB=45°;
(2)∵∠ABC=90°,AB=BD,
∴∠BAD=∠ADB=45°,
∴∠DAC+∠DCA=45°,
∵AD=CD,
∴∠DAC=∠DCA=22.5°,
∴∠BAE=∠BAD+∠DAC=67.5°,
由(1)知∠AEB=45°,
∴∠ABE=180°﹣∠AEB﹣∠BAE=67.5°,
∴∠EBC=∠ABC﹣∠ABE=90°﹣67.5°=22.5°.
12.证明:∵BC=BA,CN=BC,
∴BA=CN,
∵BC=BA,BD是AC边上的中线,
∴BD是AC边上的高线,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵CE是AB边上的高,
∴∠AEC=∠AEN=90°,
∴∠BAD+∠ACE=90°,∠BAN+∠N=90°,
∴∠ABM=∠NCA,
在△ABM与△NCA中,
,
∴△ABM≌△NCA(SAS),
∴∠MAB=∠N,
∴∠BAN+∠MAB=90°,
∴MA⊥NA.
13.(1)证明:在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=60°,,
∵DE是AB的垂直平分线,
∴,
∴AD=AC,
∴△ADC是等边三角形;
(2)证明:DE是AB的垂直平分线,
∴AE=BE,DE⊥AB,
∴∠EAB=∠B=30°,则∠EAC=∠BAC﹣∠EAB=30°,
∴∠BAE=∠CAE,
∴AE平分∠BAC,
∵DE⊥AB,AC⊥BC,
∴DE=EC,
∵△ADC是等边三角形,
∴AD=AC,
∴点E在线段CD的垂直平分线上.
14.解:(1)∵△ABC是等边三角形,E为AB的中点,
∴∠BCE=30°,BE=AE,
∵ED=EC,
∴∠EDB=∠BCE=30°,
∵∠ABD=120°,
∴∠DEB=30°,
∴DB=EB,
∴AE=DB;
(2)如图1,E在线段AB上时,
∵AB=2,AE=1,
∴点E是AB的中点,
由(1)知,BD=AE=1,
∴CD=BC+BD=3;
如图2,E在线段AB的反向延长线上时,
∵AE=1,AB=2,
∴BE=3,
∵△ABC是等边三角形,
∴∠BAC=∠BCA=60°,AB=BC=AC=2,
过E作EH∥AC交BC的延长线于H,
∴∠BEH=∠BHE=60°,
∴△BEH是等边三角形,
∴BE=EH=BH=3,∠B=∠H=60°,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠B+∠BED=∠H+∠HEC,
∴∠BED=∠HEC,
在△BDE和△HCE中,
,
∴△BDE≌△HCE(SAS),
∴BD=HC=BH﹣BC=3﹣2=1,
∴CD=BH﹣BD﹣HC=3﹣1﹣1=1.
综上所述,CD的长为1或3.
15.解:(1)∵DC平分∠ACB,
∴∠BCD=∠ACD,
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠EDC=∠ACD,
∴ED=EC,
∵点E是边AC的中点,AC=8,
∴EC=AC=4,
∴DE=4;
(2)∵DE∥BC,
∴∠ADE=∠B,∠CDE=∠BCD,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠B=∠BCD,
∴DB=DC.
如图2,作DG⊥BC于点G,
∵DB=DC,DG⊥BC,
∴GB=BC=×9=4.5,
∵∠ABC=30°,BF=DF,
∴∠BDF=∠B=30°,
∴∠DFG=∠B+∠BDF=60°,
∴∠FDG=30°,
∴BF=DF=2FG,
∴GF=1.5,
∴DF=2FG=3.
16.(1)证明:如图,连接BD、CD,
∵D是线段BC垂直平分线上的点,
∴BD=DC,
∵D是∠BAC平分线上的点,DG⊥AB,DH⊥AC,
∴DG=DH,∠DGB=∠H=90°,
在Rt△BDG与Rt△CDH中,
,
∴Rt△BDG≌Rt△CDH(HL),
∴BG=CH;
(2)解:∵Rt△ADG≌Rt△ADH(HL),
∴AG=AH,
∴AB﹣AC=AG+BG﹣(AH﹣CH)=2BG=8﹣6=2,
∴BG=1,
∴AG=AB﹣BG=8﹣1=7.
17.(1)证明:如图,连接AM,CM,
∵BM平分∠ABC,ME⊥BC于点E,MF⊥AB于点F,
∴ME=MF,
∵D为AC的中点,且MD⊥AC,
∴MA=MC,
在Rt△MAF和Rt△MCE中,
,
∴Rt△MAF≌Rt△MCE(HL),
∴AF=CE;
(2)解:在Rt△MBF和Rt△MBE中,
,
∴Rt△MBF≌Rt△MBE(HL),
∴BF=BE,
∵BC=8,AB=4,
∴BF=BE=AB+AF=4+CE,
∵BE=BC﹣CE=8﹣CE,
∴4+CE=8﹣CE,
∴CE=2,
∴BE=BC﹣CE=8﹣CE=6,
∴AF=CE=2.
∴BE,AF的长分别为6,2.
18.(1)证明:①∵∠BAC=90°,∠DAE=90°,
∴∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD.
②∵△ABD≌△ACE,
∴∠ABD=∠ACE.
在Rt△ABC中,∵∠BAC=90°,
∴∠ABC+∠ACB=90°,即∠ACB+∠ACE=90°,
∴BC⊥CE.
(2)解:①不成立.理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠BAD=∠CAE.
在△DAB与△EAC中,
∴△DAB≌△EAC(SAS),
∴DB=CE.
∵CD﹣DB=BC,
∴BC=CD﹣CE.
②成立.证明如下:
∵△DAB≌△EAC(SAS),
∴∠ABD=∠ACE.
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠ABD=∠ACE=135°,
∴∠BCE=∠ACE﹣∠ACB=135°﹣45°=90°,
即CE⊥BC.
19.解:(1)∵点P从点B出发,沿BC边以每秒1个单位长度的速度运动,到达点C后立即以每秒2个单位长度的速度返回点B,
∴点P返回点B时,共耗时为=4+2=6(秒).
故答案为6;
(2)当t=5时,BP=BC﹣PC=4﹣(5﹣4)×2=2;
(3)当点P到达点C之前,PC=4﹣t,AB=3,
∴S△ACP=AB×PC=×3×(4﹣t)=6﹣t;
(4)当△ABP是等腰三角形时,AB=BP=3,
若点P到达点C之前,BP=3,
即t=3秒时,△ABP是等腰三角形;
若点P到达点C之后,BP=3,CP=1,
即t=4+=(秒),△ABP是等腰三角形.
综合以上可得t=3或时,△ABP是等腰三角形.
20.(1)证明:∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,∠BAD=∠EAC=90°,AD=AE,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴BD=CE;
(2)解:∵△ADB≌△AEC,
∴∠ACE=∠ABD,
而在△CDF中,∠BFC=180°﹣∠ACE﹣∠CDF,
又∵∠CDF=∠BDA
∴∠BFC=180°﹣∠DBA﹣∠BDA
=∠DAB
=90°;
(3)解:BD=CE成立.理由如下:
如图2,
△ABC、△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=90°,
∵∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴BD=CE.
解答题专题训练(附答案)
1.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接AF.
(1)求证:DF=BF;
(2)连接CE,求证直线AF是线段CE的垂直平分线.
2.如图,点B、F、C、E在一条直线上,△ABC≌△DEF,连结AD交BE于O.
(1)求证:AC∥FD,AB∥ED;
(2)求证:AO=DO.
3.如图,已知,△ABC≌△ADE,AD与BC交于点F,点C在DE上,∠B=30°,∠AFC=70°.
(1)求∠FCD的度数;
(2)求证:AC=AF.
4.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当α为多少度时,△AOD是等腰三角形,请说明理由.
5.如图,在等边△ABC中,点D为边BC上一点,∠ABE=∠CAD,CF∥BE交AD的延长线于点F.
(1)求∠AEB的度数;
(2)若BE=10,AF=15,求AE的长.
6.如图,在△ABC中,AC>BC,∠A=45°,点D是AB边上一点,且CD=CB,过点B作BF⊥CD于点E,与AC交于点F点,画出∠DCB的角平分线交AB于G并回答以下问题:
(1)求证:∠ABF=∠BCD;
(2)判断△BCF的形状,并说明理由.
7.如图,△ABC和△ADE均为等边三角形,A,D,C在同一条直线上,连接BD,CE,点M,N分别为BD,CE的中点,顺次连接A,M,N.
(1)求证:BD=CE;
(2)判断△AMN的形状,并说明理由.
8.如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,连接BD,若AC=15,△BCD的周长等于25.
(1)求BC的长;
(2)若∠ADB=108°,AB=AC,求∠C的度数.
9.如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
(1)∠EAD=∠EDA;
(2)DF∥AC.
10.如图,在△ABC中,∠BAC>90°,AB的垂直平分线分别交AB,BC于点E,F,AC的垂直平分线分别交AC,BC于点M,N,直线EF,MN交于点P.
(1)求证:点P在线段BC的垂直平分线上;
(2)连接AP,求证:AP平分∠FAN;
(3)设∠FAN=α,其他条件不变时,∠FPN的度数是 .(用含α的代数式表示)
11.如图,在直角△ABC中,∠ABC=90°,边BC上有一点D满足AB=BD,过点D作DE⊥AC于点E,连接BE.
(1)如图1,在EA延长线上取AM=ED,连接BM.求证:∠AEB=45°.
(2)如图2,连接AD,若AD=CD,求∠EBC的度数.
12.如图,在△ABC中,BC=BA,BD是AC边上的中线,在射线BD上截取BM=AC,CE是AB边上的高,在射线CE上截取CN=BC,联结MA、NA,求证:MA⊥NA.
13.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,DE是AB的垂直平分线,交AB、BC于点D、E连接CD、AE.求证:
(1)△ADC是等边三角形;
(2)点E在线段CD的垂直平分线上.
14.如图,在等边△ABC中,已知点E在直线AB上(不与点A、B重合),点D在直线BC上,且ED=EC.
(1)若点E为线段AB的中点时,试说明DB=AE的理由;
(2)若△ABC的边长为2,AE=1,求CD的长.
15.已知△ABC中,∠ACB的平分线CD交AB于点D,DE∥BC.
(1)如图1,如果点E是边AC的中点,AC=8,求DE的长;
(2)如图2,若DE平分∠ADC,∠ABC=30°,在BC边上取点F使BF=DF,若BC=9,求DF的长.
16.如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线交于点D,DG⊥AB,DH⊥AC,G,H为垂足.
(1)求证:BG=CH;
(2)若AB=8,AC=6,求AG的长.
17.如图,BM平分∠ABC,D为AC的中点,且MD⊥AC,过点M作ME⊥BC于点E,MF⊥AB于点F.
(1)求证:AF=CE;
(2)如果BC=8,AB=4,求BE,AF的长.
18.在△ABC中,AB=AC,∠BAC=90°,点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰直角三角形ADE,使∠DAE=90°,AD=AE.
(1)当点D在线段BC上时,如图①,求证:①BC=CE+CD;②CE⊥BC.
(2)当点D在线段CB的延长线上时,如图②,(1)中的两个结论是否仍然成立.若成立,请给予证明;若不成立,请说明理由.
19.如图,在△ABC中,∠B=90°,AB=3,BC=4.点P从点B出发,沿BC边以每秒1个单位长度的速度运动,到达点C后立即以每秒2个单位长度的速度返回点B,点P运动的时间为t秒.
(1)点P返回点B时,共耗时 秒;
(2)当t=5时,求BP的长;
(3)当点P到达点C之前,求△ACP的面积(用含t的代数式表示);
(4)当△ABP是等腰三角形时,直接写出t的值.
20.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.
(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,只探究BD与CE之间的关系.(只写结论,不必说明理由)
参考答案
1.证明:(1)∵Rt△ABC≌Rt△ADE,
∴AB=AD,
在Rt△ADF与Rt△ABF中,
,
∴Rt△ADF≌Rt△ABF(HL),
∴DF=BF;
(2)连接CE,∵Rt△ABC≌Rt△ADE,
∴BC=DE,AC=AE,
∵DF=BF,
∴FC=FE,
∴点A和点F在CE的中垂线上,
∴AF是CE的中垂线.
2.(1)证明:∵△ABC≌△DEF,
∴∠B=∠E,∠ACB=∠EFD,
∴AB∥DE,AC∥DF;
(2)证明:∵△ABC≌△DEF,
∴∠ACB=∠EFD,AC=DF,
在△ACO和△DFO中,
,
∴△ACO≌△DFO(AAS),
∴AO=DO.
3.(1)解:∵△ABC≌△ADE,
∴∠B=∠D=30°,
∵∠AFC=70°,
∴∠FCD=∠AFC﹣∠D=70°﹣30°=40°;
(2)证明:∵△ABC≌△ADE,
∴AE=AC,∠E=∠ACB,
∴∠E=∠ACE=∠ACB,
由(1)知,∠FCD=40°,
∴∠ACF=(180°﹣∠FCD)=(180°﹣40°)=70°,
∵∠AFC=70°,
∴∠ACF=∠AFC,
∴AC=AF.
4.解:(1)△AOD是直角三角形,理由如下:
∵△BOC≌△ADC,∠α=150°,
∴OC=DC,∠ADC=∠BOC=∠α=150°,
∵∠OCD=60°,
∴△OCD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形;
(2)当α=110°或125°或140°时,△AOD是等腰三角形,理由如下:
∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.
5.解:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∵∠ABE=∠CAD,
∴∠CAD+∠BAE=∠ABE+∠BAE=∠BAC=60°,
∴∠AEB=120°;
(2)如图,在AF上截取FH=FC,连接CH,
∵∠AEB=120°,
∴∠BED=60°,
∵BE∥CF,
∴∠BED=∠F=60°,
又∵FH=FC,
∴△FCH是等边三角形,
∴CF=CH=FH,∠FCH=∠FHC=60°,
∴∠AHC=120°=∠AEB,
在△ABE和△CAH中,
,
∴△ABE≌△CAH(AAS),
∴BE=AH=10,AE=CH,
∴FH=CH=AE=5.
6.(1)证明:过点C作CG⊥AB于点G,
∴∠DCG+∠CDG=90°,
∵BC=DC,
∴∠BCG=∠DCG=∠BCD,
∵BF⊥CD于点E,
∴∠ABF+∠CDG=90°,
∴∠ABF=∠DCG=∠BCD;
(2)解:△BCF是等腰三角形,
理由:如图,∵∠A=45°,CG⊥AB,
∴∠ACG=45°,
∵∠ACB=∠ACG+∠BCG,∠BFC=∠A+∠ABF,
∴∠ACB=45°+∠BCG,∠BFC=45°+∠ABF,
∵∠BCG=∠DCG=∠ABF,
∴∠BCF=∠BFC,
∴BC=BF,
∴△BCF是等腰三角形.
7.证明:(1)∵△ABC和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)△AMN是等边三角形,
理由如下:
∵点M,N分别为BD,CE的中点,BD=CE,
∴BM=CN,
∵△ABD≌△ACE,
∴∠ABM=∠ACN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴AM=AN,∠BAM=∠CAN,
∴∠MAN=∠BAC﹣∠BAM+∠CAN=60°,
∴△AMN是等边三角形.
8.解:(1)∵MN是AB的垂直平分线,
∴AD=BD,
∵AC=15,△BCD的周长等于25,
∴BC+CD+BD=BC+CD+AD=BC+AC=25,
∴BC=10.
(2)∵MN是AB的垂直平分线,∠ADB=108°,
∴,∠AED=90°.
∴∠A=36°,
∵AB=AC,
∴.
9.证明:(1)∵EF是AD的垂直平分线,
∴EA=ED,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴FA=FD,
∴∠FDA=∠FAD,
∵AD平分∠BAC,
∴∠FAD=∠CAD,
∴∠FDA=∠CAD,
∴DF∥AC.
10.(1)证明:如图,连接PA,PB,PC.
∵PE垂直平分AB,PM垂直平分AC,
∴PA=PB,PA=PC,
∴PB=PC,
∴点P在线段BC的垂直平分线上.
(2)证明:由(1)知PB=PC,
∴∠PBF=∠PCN,
∵PE垂直平分AB,
∴PA=PB,FA=FB,
∴∠PAB=∠PBA,∠FAB=∠FBA,
∴∠PAF=∠PBF,
同理∠PAN=∠PCN,
∴∠PAF=∠PAN,即AP平分∠FAN.
(3)解:∵PE垂直平分AB,PM垂直平分AC,
∴FA=FB,NA=NC,∠AEP=∠AMP=90°,
设∠B=x,∠C=y,
∴∠B=x=∠BAF,∠C=y=∠CAN,
在△ABC中,∠B+∠C+∠CAB=180°,∠FAN=α,
∴x+y+x+y+α=180°,即,
在四边形AEPM中,∠AEP+∠AMP+∠EAM+∠FPN=360°,
∴,
故答案为:.
11.(1)证明:∵DE⊥AC,
∴∠DEC=90°=∠ABC,
∴∠DEC+∠C=∠ABC+∠C,即∠BDE=∠MAB,
∵AB=BD,AM=DE,
∴△MAB≌△EDB(SAS),
∴∠MBA=∠EBD,BM=BE,
∴∠MBA+∠ABE=∠EBD+∠ABE=∠ABC=90°,即∠MBE=90°,
∴△MBE是等腰直角三角形,
∴∠AEB=45°;
(2)∵∠ABC=90°,AB=BD,
∴∠BAD=∠ADB=45°,
∴∠DAC+∠DCA=45°,
∵AD=CD,
∴∠DAC=∠DCA=22.5°,
∴∠BAE=∠BAD+∠DAC=67.5°,
由(1)知∠AEB=45°,
∴∠ABE=180°﹣∠AEB﹣∠BAE=67.5°,
∴∠EBC=∠ABC﹣∠ABE=90°﹣67.5°=22.5°.
12.证明:∵BC=BA,CN=BC,
∴BA=CN,
∵BC=BA,BD是AC边上的中线,
∴BD是AC边上的高线,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵CE是AB边上的高,
∴∠AEC=∠AEN=90°,
∴∠BAD+∠ACE=90°,∠BAN+∠N=90°,
∴∠ABM=∠NCA,
在△ABM与△NCA中,
,
∴△ABM≌△NCA(SAS),
∴∠MAB=∠N,
∴∠BAN+∠MAB=90°,
∴MA⊥NA.
13.(1)证明:在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=60°,,
∵DE是AB的垂直平分线,
∴,
∴AD=AC,
∴△ADC是等边三角形;
(2)证明:DE是AB的垂直平分线,
∴AE=BE,DE⊥AB,
∴∠EAB=∠B=30°,则∠EAC=∠BAC﹣∠EAB=30°,
∴∠BAE=∠CAE,
∴AE平分∠BAC,
∵DE⊥AB,AC⊥BC,
∴DE=EC,
∵△ADC是等边三角形,
∴AD=AC,
∴点E在线段CD的垂直平分线上.
14.解:(1)∵△ABC是等边三角形,E为AB的中点,
∴∠BCE=30°,BE=AE,
∵ED=EC,
∴∠EDB=∠BCE=30°,
∵∠ABD=120°,
∴∠DEB=30°,
∴DB=EB,
∴AE=DB;
(2)如图1,E在线段AB上时,
∵AB=2,AE=1,
∴点E是AB的中点,
由(1)知,BD=AE=1,
∴CD=BC+BD=3;
如图2,E在线段AB的反向延长线上时,
∵AE=1,AB=2,
∴BE=3,
∵△ABC是等边三角形,
∴∠BAC=∠BCA=60°,AB=BC=AC=2,
过E作EH∥AC交BC的延长线于H,
∴∠BEH=∠BHE=60°,
∴△BEH是等边三角形,
∴BE=EH=BH=3,∠B=∠H=60°,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠B+∠BED=∠H+∠HEC,
∴∠BED=∠HEC,
在△BDE和△HCE中,
,
∴△BDE≌△HCE(SAS),
∴BD=HC=BH﹣BC=3﹣2=1,
∴CD=BH﹣BD﹣HC=3﹣1﹣1=1.
综上所述,CD的长为1或3.
15.解:(1)∵DC平分∠ACB,
∴∠BCD=∠ACD,
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠EDC=∠ACD,
∴ED=EC,
∵点E是边AC的中点,AC=8,
∴EC=AC=4,
∴DE=4;
(2)∵DE∥BC,
∴∠ADE=∠B,∠CDE=∠BCD,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠B=∠BCD,
∴DB=DC.
如图2,作DG⊥BC于点G,
∵DB=DC,DG⊥BC,
∴GB=BC=×9=4.5,
∵∠ABC=30°,BF=DF,
∴∠BDF=∠B=30°,
∴∠DFG=∠B+∠BDF=60°,
∴∠FDG=30°,
∴BF=DF=2FG,
∴GF=1.5,
∴DF=2FG=3.
16.(1)证明:如图,连接BD、CD,
∵D是线段BC垂直平分线上的点,
∴BD=DC,
∵D是∠BAC平分线上的点,DG⊥AB,DH⊥AC,
∴DG=DH,∠DGB=∠H=90°,
在Rt△BDG与Rt△CDH中,
,
∴Rt△BDG≌Rt△CDH(HL),
∴BG=CH;
(2)解:∵Rt△ADG≌Rt△ADH(HL),
∴AG=AH,
∴AB﹣AC=AG+BG﹣(AH﹣CH)=2BG=8﹣6=2,
∴BG=1,
∴AG=AB﹣BG=8﹣1=7.
17.(1)证明:如图,连接AM,CM,
∵BM平分∠ABC,ME⊥BC于点E,MF⊥AB于点F,
∴ME=MF,
∵D为AC的中点,且MD⊥AC,
∴MA=MC,
在Rt△MAF和Rt△MCE中,
,
∴Rt△MAF≌Rt△MCE(HL),
∴AF=CE;
(2)解:在Rt△MBF和Rt△MBE中,
,
∴Rt△MBF≌Rt△MBE(HL),
∴BF=BE,
∵BC=8,AB=4,
∴BF=BE=AB+AF=4+CE,
∵BE=BC﹣CE=8﹣CE,
∴4+CE=8﹣CE,
∴CE=2,
∴BE=BC﹣CE=8﹣CE=6,
∴AF=CE=2.
∴BE,AF的长分别为6,2.
18.(1)证明:①∵∠BAC=90°,∠DAE=90°,
∴∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD.
②∵△ABD≌△ACE,
∴∠ABD=∠ACE.
在Rt△ABC中,∵∠BAC=90°,
∴∠ABC+∠ACB=90°,即∠ACB+∠ACE=90°,
∴BC⊥CE.
(2)解:①不成立.理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠BAD=∠CAE.
在△DAB与△EAC中,
∴△DAB≌△EAC(SAS),
∴DB=CE.
∵CD﹣DB=BC,
∴BC=CD﹣CE.
②成立.证明如下:
∵△DAB≌△EAC(SAS),
∴∠ABD=∠ACE.
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠ABD=∠ACE=135°,
∴∠BCE=∠ACE﹣∠ACB=135°﹣45°=90°,
即CE⊥BC.
19.解:(1)∵点P从点B出发,沿BC边以每秒1个单位长度的速度运动,到达点C后立即以每秒2个单位长度的速度返回点B,
∴点P返回点B时,共耗时为=4+2=6(秒).
故答案为6;
(2)当t=5时,BP=BC﹣PC=4﹣(5﹣4)×2=2;
(3)当点P到达点C之前,PC=4﹣t,AB=3,
∴S△ACP=AB×PC=×3×(4﹣t)=6﹣t;
(4)当△ABP是等腰三角形时,AB=BP=3,
若点P到达点C之前,BP=3,
即t=3秒时,△ABP是等腰三角形;
若点P到达点C之后,BP=3,CP=1,
即t=4+=(秒),△ABP是等腰三角形.
综合以上可得t=3或时,△ABP是等腰三角形.
20.(1)证明:∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,∠BAD=∠EAC=90°,AD=AE,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴BD=CE;
(2)解:∵△ADB≌△AEC,
∴∠ACE=∠ABD,
而在△CDF中,∠BFC=180°﹣∠ACE﹣∠CDF,
又∵∠CDF=∠BDA
∴∠BFC=180°﹣∠DBA﹣∠BDA
=∠DAB
=90°;
(3)解:BD=CE成立.理由如下:
如图2,
△ABC、△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=90°,
∵∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△ADB和△AEC中,
,
∴△ADB≌△AEC(SAS),
∴BD=CE.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
