22.1.2 二次函数y=ax2的应用随堂过关练习(含答案)
文档属性
| 名称 | 22.1.2 二次函数y=ax2的应用随堂过关练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 316.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 00:00:00 | ||
图片预览

文档简介
二次函数y=ax 的应用随堂过关练习
一、选择题(本大题共6小题,每小题3分,共18分)
1. 对于抛物线y=x -与y = -x ,下列说法错误的是( ).
A. 两条抛物线关于 x 轴对称 B. 两条抛物线关于坐标原点对称
C. 两条抛物线各自关于 y轴对称 D. 两条抛物线没有公共点
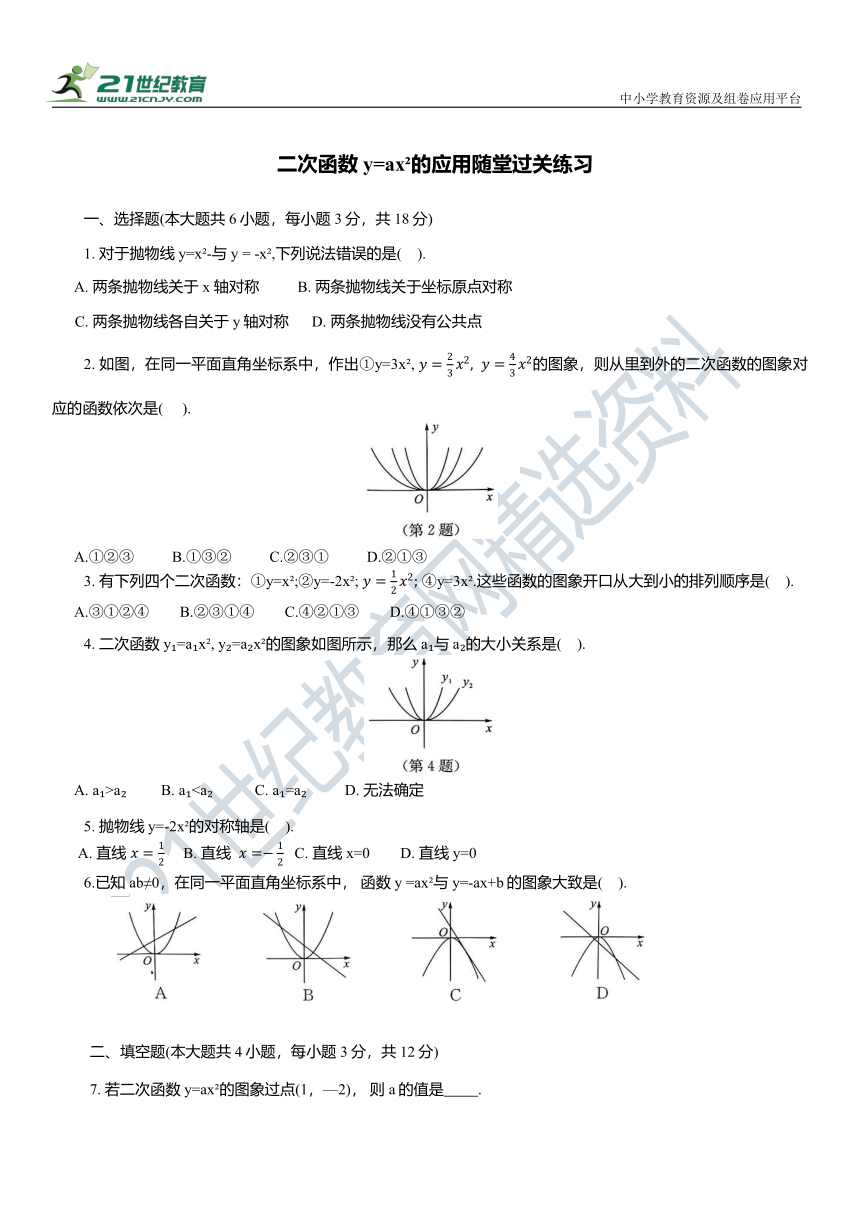
2. 如图,在同一平面直角坐标系中,作出①y=3x , 的图象,则从里到外的二次函数的图象对应的函数依次是( ).
A.①②③ B.①③② C.②③① D.②①③
3. 有下列四个二次函数:①y=x ;②y=-2x ; ④y=3x .这些函数的图象开口从大到小的排列顺序是( ).
A.③①②④ B.②③①④ C.④②①③ D.④①③②
4. 二次函数y =a x , y =a x 的图象如图所示,那么a 与a 的大小关系是( ).
A. a >a B. a 5. 抛物线y=-2x 的对称轴是( ).
A. 直线 B. 直线 C. 直线x=0 D. 直线y=0
6.已知ab≠0,在同一平面直角坐标系中, 函数y =ax 与y=-ax+b的图象大致是( ).
二、填空题(本大题共4小题,每小题3分,共12分)
7. 若二次函数y=ax 的图象过点(1,—2), 则a的值是 .
8.已知A( ,b);是抛物线y=x 上的一点,过点A作x轴的平行线交抛物线于另一点B, 则点B 的坐标是 .
9. 如图,A, B分别为抛物线y =ax 上的两点, 且AB⊥y轴于点(0, 6). 若AB=6, 则该抛物线的解析式为 .
10. 当m= 时, 抛物线 开口向下.
三、解答题(本大题共2小题,每小题 10分,共20分. 解答时应写出必要的文字说明、证明过程或演算步骤)
11. 已知二次函数y=ax 的图象与直线y=2x-3交于点 P(1, b).
(1)求a,b的值;
(2)写出二次函数的解析式,并指出x取何值时,该函数的y随x的增大而减小.
12. 已知抛物线y=ax 与直线y=x+2交于点A(m, 1),
(1)求抛物线的解析式;
中小学教育资源及组卷应用平台
(2)设抛物线与直线y=x+2的另一交点为 B,求点B 的坐标和△AOB 的面积.
1. D 2. B 3. A 4. A 5. C 6. B
7.-2 8.(- , ) 10. -1
11. (1)b= -1, a =-1.
(2)二次函数的解析式为y= -x ,当x>0时,该函数的y随x的增大而减小.
12. (1)y=x . (2)点B(2,4),S△AOB =3.
一、选择题(本大题共6小题,每小题3分,共18分)
1. 对于抛物线y=x -与y = -x ,下列说法错误的是( ).
A. 两条抛物线关于 x 轴对称 B. 两条抛物线关于坐标原点对称
C. 两条抛物线各自关于 y轴对称 D. 两条抛物线没有公共点
2. 如图,在同一平面直角坐标系中,作出①y=3x , 的图象,则从里到外的二次函数的图象对应的函数依次是( ).
A.①②③ B.①③② C.②③① D.②①③
3. 有下列四个二次函数:①y=x ;②y=-2x ; ④y=3x .这些函数的图象开口从大到小的排列顺序是( ).
A.③①②④ B.②③①④ C.④②①③ D.④①③②
4. 二次函数y =a x , y =a x 的图象如图所示,那么a 与a 的大小关系是( ).
A. a >a B. a 5. 抛物线y=-2x 的对称轴是( ).
A. 直线 B. 直线 C. 直线x=0 D. 直线y=0
6.已知ab≠0,在同一平面直角坐标系中, 函数y =ax 与y=-ax+b的图象大致是( ).
二、填空题(本大题共4小题,每小题3分,共12分)
7. 若二次函数y=ax 的图象过点(1,—2), 则a的值是 .
8.已知A( ,b);是抛物线y=x 上的一点,过点A作x轴的平行线交抛物线于另一点B, 则点B 的坐标是 .
9. 如图,A, B分别为抛物线y =ax 上的两点, 且AB⊥y轴于点(0, 6). 若AB=6, 则该抛物线的解析式为 .
10. 当m= 时, 抛物线 开口向下.
三、解答题(本大题共2小题,每小题 10分,共20分. 解答时应写出必要的文字说明、证明过程或演算步骤)
11. 已知二次函数y=ax 的图象与直线y=2x-3交于点 P(1, b).
(1)求a,b的值;
(2)写出二次函数的解析式,并指出x取何值时,该函数的y随x的增大而减小.
12. 已知抛物线y=ax 与直线y=x+2交于点A(m, 1),
(1)求抛物线的解析式;
中小学教育资源及组卷应用平台
(2)设抛物线与直线y=x+2的另一交点为 B,求点B 的坐标和△AOB 的面积.
1. D 2. B 3. A 4. A 5. C 6. B
7.-2 8.(- , ) 10. -1
11. (1)b= -1, a =-1.
(2)二次函数的解析式为y= -x ,当x>0时,该函数的y随x的增大而减小.
12. (1)y=x . (2)点B(2,4),S△AOB =3.
同课章节目录
