2008年中考能力型试题专项训练 (16页无答案)
文档属性
| 名称 | 2008年中考能力型试题专项训练 (16页无答案) |  | |
| 格式 | rar | ||
| 文件大小 | 147.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-24 12:17:00 | ||
图片预览




文档简介
跟蒋老师学数学 彰显数学魅力 呈现三维目标 电话:13542799054
能力型试题专项训练
一、方程与方程组
1.一元一次方程根的判别式与韦达定理综合题
例1. 已知一元二次方程有两个实数根,在数轴上表示的点在表示的点的右边,且距离为,求的值
例2.已知关于x的一元二次方程的两实根的倒数和大于零,求的取值范围
例3.已知函数的图像与轴的支点为,求的值
例4. 是否存在常数,使关于的方程的两个实根满足?如果存在,求出所有满足条件的k的值,如果不存在,请说明理由
例5.已知关于的方程有两个非0实根,问是否能同号,求出相应的m的取值范围,若不能同号,请说明理由
例6.已知关于的方程为(
(1).求证:此方程总有实数根
(2).当方程有两个实数根,且两根平方和为4时,求的值
例7.已知k为正整数,关于的一元二次方程有两个不相等实数根
(1).求k的值
(2).若一次函数与反比例函数的图像都经过点,
求这个一次函数和反比例的解析式。
例8.已知关于的一元二次方程
(1).求证:不论k为何值,方程总有两个不相等的实根
(2).设是方程两根,且,求k的值
例9.已知是关于的二次方程的两个实数根,是关于y的二次方程的两个实数根,且,求的值
例10.已知关于的方程=0
(1).求证:方程总有两个实数根
(2).设方程两个实数根为,且, 求的
2.方程与几何综合题
例11.如图,O为线段AB上一点,以OB为半径的圆O交AB于点C,以AO为直径的半圆交圆O于点C,过B作 BEAB交AD于E
(1).求证:AE切圆O于点D
(2).若AC=2,且AC,AD的长是关于x的方程=0的两根,求EB的长
(3).当点O位于AB上何处时ODC恰好为等边三角形。
例12.已知方程有两个相等实根,是的三边,且
(1).求
(2).若上述三角形最短边为5,而方程的两根平方和为最长边的3倍,求m 的值
例13.如图,在中,,为上一点,以O为圆心,OB为半径的半圆交AB于E,与
AC切于点D,AD=2,AE=1
求证:是方程的两个根
例14.如图,在梯形ABCD中,AD//BC,AD=AB,AE是高,且AE= ,,
(1).求
(2).设点M是对角线AC上一点,DM的延长线交BC与F,当时,求作以CF,DF的长为根的一元二次方程
例15.如图,AD是圆O的直径,直线交圆O于E、F两点,作AB于B,DC于C,CD交圆O于G
(1).求证:
(2).设AB=m,BC=n,CD=p,求证:是方程的两个根
(3).若(2)中方程满足,判断与圆O的位置关系
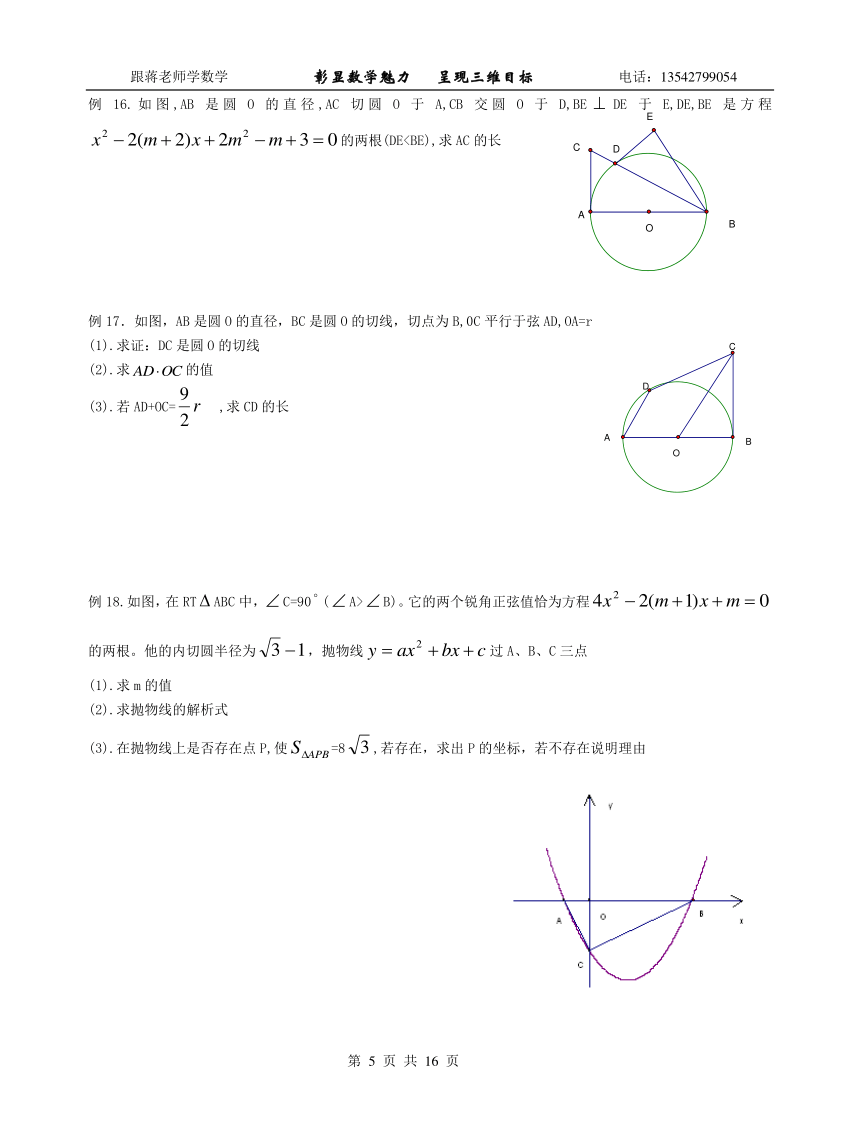
例16.如图,AB是圆O的直径,AC切圆O于A,CB交圆O于D,BEDE于E,DE,BE是方程的两根(DE例17.如图,AB是圆O的直径,BC是圆O的切线,切点为B,0C平行于弦AD,OA=r
(1).求证:DC是圆O的切线
(2).求的值
(3).若AD+OC= ,求CD的长
例18.如图,在RTABC中,C=90(A>B)。它的两个锐角正弦值恰为方程的两根。他的内切圆半径为,抛物线过A、B、C三点
(1).求m的值
(2).求抛物线的解析式
(3).在抛物线上是否存在点P,使=8,若存在,求出P的坐标,若不存在说明理由
二. 函数型综合题
1.函数与方程
例19.在平面直角坐标系内,O为坐标原点,二次函数的图像交x轴于点
,且
(1).求二次函数的解析式
(2).若将上述二次函数图像沿x轴向右平移2个单位,设平移后图像与y轴交点为X.顶点为p,求的面积。
例20.在RTABC中, ACB=90,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴建立直角坐标系,若,且线段OA,OB的长度是关于x的一元二次方程的两根
(1).求C点坐标
(2).以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E三点的抛物线的解析式
(3).抛物线上是否存在点P,使得与全等?若存在,求出符合条点的P点。若不存在,说明理由
例21.如图,在平面直角坐标系内,RTABC斜边AB在x轴上,点C坐标为(0,6),AB =15,CBA>CAB.
且tanCAB,tanCBA是关于x的方程的两根
(1).求m和n的值。
(2).若ACB的平分线交x轴于D.求直线CD的解析式
(3).在(2)的条件下,直线CD上是否存在点M,过点M做BC平行线,交y轴于N,使以M,N,B,C为顶点的四边形是平行四边形。若存在,请直接写出M的坐标,若不存在请说明理由
例22.如图,直径为13的圆O经过原点O,并且与x轴、y轴分别交于点A、B两点,线段OA、OB的长(OA>OB)是方程的两根
(1).求线段OA,OB的长
(2).已知C在劣弧OA上,连接BC交OA于D,当时,求点C的坐标
(3).在圆上是否存在点P,使得.若存在,求出P的坐标,若不存在,说明理由
2.函数与几何
例23.在中, ,圆A的半径为1。若点0在BC上运动(与b,c点不重合),设OB=x,AOC面积为y.
(1).求y关于x的函数解析式,并写出函数的定义域
(2).以0为圆心,BO长为半径做圆0,当圆0与圆A相切时,求AOC的面积
例24.如图,圆A与圆B外切于点C,DE是两圆的一条外公切线,切点为d、E.
(1).判断的形状并证明
(2).过C作C0De于E,以直线DE为x轴,OC为y轴建立直角坐标系,且OE=2,OD=8.求过D、C、E三点的抛物线的解析式,并求出抛物线的顶点坐标
(3).该抛物线定点是否在连心线AB上?如果在,请证明,如果不在说明理由
例25.如图,在ABC中,AC=14,Bc=,=45.点O在AC上移动,圆O始终与AB相切。切点为D.圆O与AC相交于E、F(F可能在AC延长线上)
(1).设圆O半径为r,在满足题意的点O中是否存在某一位置,使得圆O与AB,BF都相切?若不存在,说明理由,若存在,求出此时r的长
(2).设四边形BDOC的面积为S.求S与r的函数关系式及r的取值范围
例26.如图,圆O与x轴交于A,B两点,与y轴交于C,D两点,圆心坐标为(1,-1),半径为
(1).比较线段AB与CD的大小。
(2).求A、B、C、D四点的坐标
(3).过D作圆的切线,求这条切线的解析式
三.几何综合题
1.线段的相等关系、比例关系的证明
例27.如图,MN切圆O于P,AB是圆O的弦,于M,BNMN于N,PQAB于Q
求证:PQ=
例28.如图,PA为圆O的切线,A为切点,PBC为割线,APC的平分线交AB于D,交AC于E
(1).求证:AD=AE
(2).求证:
例29.如图,BC是圆O的直径,ADBC于D,过B作弦BF交AD于E,交圆于F,交AC于H,且AE=BE
(2).
例30.如图,圆与圆相交于A、B两点,点在圆上,过A的直线交两圆于C、D.过B点的直线
交两圆于E、F.AB与相交于P
求证:(1).CE//DF
(2).
例31.如图,已知弦AB等于圆O的半径,连接OB并延长使BC=OB
(1).求证:AC是圆O的切线
(2).请在圆上取点D,使AD=AC(自己完成作图并给出证明过程)
例32.如图,两圆内切于点P,大圆的弦切小圆于C,PC的延长线交大圆于D
求证:(1).APD=BPD
(2).
例33.如图,内接于圆O,AB延长线与过C点的切线GC相交于点D,BE与AC相交于点F.且CB=CE.
求证:(1).BE//DG
(2)
2.几何的证明与计算题
例34.如图,PAB是圆O的割线,AB是圆O的直径,PC为圆O的切线,C为切点,BDPC于点D.交圆O于E.PA=AO=OB=1
(1).求P的度数。(2).求DE的长
例35.如图,圆O的内接ABC中,.AB=AC,D是圆O上一点,AD延长线交BC的延长线于P.
(1).求证:
(2).若圆O的直径为25,AB=20,AD=15,求PC和DC的长
例36..如图,PAQ是直角,半径为5的圆O与AP相切于点T.与AQ相交于点B、C.
(1).BT是否平分OBA 证明你的结论
(2).若已知At=4,求AB的长
例37.已知如图,圆O是ABC的外接圆,且AB=Ac=13,Bc=24.PA切圆O于a.割线PBD过圆心,交圆O于点B、D.连接CD
(1).求证:PA//Bc
(2).求圆O的半径及Cd的长。
例38.如图,梯形abcd中,AD//BC,AD=2,BC=4,对角线AC=5,Bd=3,试求该梯形的面积
6例39..如图,RTABC中,C=,以BC为直径的圆O交AB于点D,连接Od并延长交CA的延长线于点E.过D作DFOE交EC点于F.
(1).求证:AF=CF
(2).若eD=2,,求AD的长
例40.已知,如图,四边形AbcD内接于圆o,AB是圆o的直径,ce切圆o于e,aece.,交圆o于D
(1).求证:DC=BC.
(2).若DC:AB=3:5,求sinCAD的值
四.代数、几何综合题
1.圆与直线综合题
例41).如图,直线与x轴,y轴分别交于点A、B,OA=4,且OA,OB的长是关于x的方程的两个根。以OB为直径的圆M交AB于C.连接CM并延长交x轴于N
(1).求AB的解析式.
(2).求线段AC的长.
(3)求证:
(4).如果D是OA的中点,求证CD是圆M的切线
例42.如图,在直角坐标系中,以(a,0)为圆心的圆与x轴交于C、D两点,与y轴交于A、B两点。
连接AC
(1).点E在AB上,EA=EC,求证:
(2).在(1)的结论下,延长EC到P,连接PB,若PB=PE,试判断PB与圆的位置关系,并说明理由
(3).如果a=2,圆半径为4,求(2)中直线PB的解析式。
2.圆与方程综合
例43.如图,,PB=PM
求证:(1).是等边三角形
(2).PA,PB是关于x的方程的两根
例44..在中,AB=,AC=6,BC=,P是AC上与A、C不重合的一动点,过P、B、C的圆O交AB于D
(1).设,求y与x的函数关系式,并确定x的取值范围
(2).P在AC上何处时y有最小值?最小值是多少?
(3).求y取最小值时圆O的面积
例45.如图,两同心圆,大圆的弦AD交小圆于B、C,AE切小圆于E,连接CE,直线BE交大圆于P、Q.
已知BE=AE, AB=a,AE=b.
(1).求证:CD、CE的长是方程的两根
(2).求PB的长
例46.如图,以RtABC的直角顶点C为原点,以两条直角边AC.AB为x轴、y轴建立直角坐标系,圆O是ABC的内切圆,半径为r.两条直角边a、b是一元二次方程的两根。AB=c
(1).确定c与r的关系,c与m的关系
(2).当圆O面积为4时,求c和m的值
(3).求在(2)的条件下直线EF的解析式
2.圆与二次函数的综合题
例47.如图,抛物线交x轴的正方向于A、B亮点,交y轴的正方向于C点。经过A、B、C三点作圆O.若圆O与y轴相切
(1).求a、c满足的关系式
(2).设ACB=,求
(3).设抛物线顶点为P判断直线PA与圆O的位置关系
例48.如图,直线y=-x+1与两轴分别交于A、B两点,以AB为边长在第一象限内作正三角形ABC.圆为ABC的外接圆与x轴交于另一点E
(1).求C点坐标
(2).求过C点与AB中点的直线的解析式
(3).求过点E、、A三点的二次函数的解析式
例4.9如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4).与x轴相交于A、B两点,且AB=6
(1).求sinACB的值
(2)求经过C、A、B三点的抛物线的解析式
(3)设抛物线的顶点为F,判断直线FA与圆D的关系
例50.如图,AB是弦,CD是直径,ABCD于H,点P在DC延长线上,且PAH=POA,OH:HC=1:2,PC=6
(1).求证:PA是圆O的切线
(2).求圆O的半径的长
(3).试在弧ACB上取一点E(E与A、B不重合).并延长PE与弧ADB交于F,设FH=x,PF=y,求y与x之间的解析式,并指出x的取值范围。
第 1 页 共 16 页
能力型试题专项训练
一、方程与方程组
1.一元一次方程根的判别式与韦达定理综合题
例1. 已知一元二次方程有两个实数根,在数轴上表示的点在表示的点的右边,且距离为,求的值
例2.已知关于x的一元二次方程的两实根的倒数和大于零,求的取值范围
例3.已知函数的图像与轴的支点为,求的值
例4. 是否存在常数,使关于的方程的两个实根满足?如果存在,求出所有满足条件的k的值,如果不存在,请说明理由
例5.已知关于的方程有两个非0实根,问是否能同号,求出相应的m的取值范围,若不能同号,请说明理由
例6.已知关于的方程为(
(1).求证:此方程总有实数根
(2).当方程有两个实数根,且两根平方和为4时,求的值
例7.已知k为正整数,关于的一元二次方程有两个不相等实数根
(1).求k的值
(2).若一次函数与反比例函数的图像都经过点,
求这个一次函数和反比例的解析式。
例8.已知关于的一元二次方程
(1).求证:不论k为何值,方程总有两个不相等的实根
(2).设是方程两根,且,求k的值
例9.已知是关于的二次方程的两个实数根,是关于y的二次方程的两个实数根,且,求的值
例10.已知关于的方程=0
(1).求证:方程总有两个实数根
(2).设方程两个实数根为,且, 求的
2.方程与几何综合题
例11.如图,O为线段AB上一点,以OB为半径的圆O交AB于点C,以AO为直径的半圆交圆O于点C,过B作 BEAB交AD于E
(1).求证:AE切圆O于点D
(2).若AC=2,且AC,AD的长是关于x的方程=0的两根,求EB的长
(3).当点O位于AB上何处时ODC恰好为等边三角形。
例12.已知方程有两个相等实根,是的三边,且
(1).求
(2).若上述三角形最短边为5,而方程的两根平方和为最长边的3倍,求m 的值
例13.如图,在中,,为上一点,以O为圆心,OB为半径的半圆交AB于E,与
AC切于点D,AD=2,AE=1
求证:是方程的两个根
例14.如图,在梯形ABCD中,AD//BC,AD=AB,AE是高,且AE= ,,
(1).求
(2).设点M是对角线AC上一点,DM的延长线交BC与F,当时,求作以CF,DF的长为根的一元二次方程
例15.如图,AD是圆O的直径,直线交圆O于E、F两点,作AB于B,DC于C,CD交圆O于G
(1).求证:
(2).设AB=m,BC=n,CD=p,求证:是方程的两个根
(3).若(2)中方程满足,判断与圆O的位置关系
例16.如图,AB是圆O的直径,AC切圆O于A,CB交圆O于D,BEDE于E,DE,BE是方程的两根(DE
(1).求证:DC是圆O的切线
(2).求的值
(3).若AD+OC= ,求CD的长
例18.如图,在RTABC中,C=90(A>B)。它的两个锐角正弦值恰为方程的两根。他的内切圆半径为,抛物线过A、B、C三点
(1).求m的值
(2).求抛物线的解析式
(3).在抛物线上是否存在点P,使=8,若存在,求出P的坐标,若不存在说明理由
二. 函数型综合题
1.函数与方程
例19.在平面直角坐标系内,O为坐标原点,二次函数的图像交x轴于点
,且
(1).求二次函数的解析式
(2).若将上述二次函数图像沿x轴向右平移2个单位,设平移后图像与y轴交点为X.顶点为p,求的面积。
例20.在RTABC中, ACB=90,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴建立直角坐标系,若,且线段OA,OB的长度是关于x的一元二次方程的两根
(1).求C点坐标
(2).以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E三点的抛物线的解析式
(3).抛物线上是否存在点P,使得与全等?若存在,求出符合条点的P点。若不存在,说明理由
例21.如图,在平面直角坐标系内,RTABC斜边AB在x轴上,点C坐标为(0,6),AB =15,CBA>CAB.
且tanCAB,tanCBA是关于x的方程的两根
(1).求m和n的值。
(2).若ACB的平分线交x轴于D.求直线CD的解析式
(3).在(2)的条件下,直线CD上是否存在点M,过点M做BC平行线,交y轴于N,使以M,N,B,C为顶点的四边形是平行四边形。若存在,请直接写出M的坐标,若不存在请说明理由
例22.如图,直径为13的圆O经过原点O,并且与x轴、y轴分别交于点A、B两点,线段OA、OB的长(OA>OB)是方程的两根
(1).求线段OA,OB的长
(2).已知C在劣弧OA上,连接BC交OA于D,当时,求点C的坐标
(3).在圆上是否存在点P,使得.若存在,求出P的坐标,若不存在,说明理由
2.函数与几何
例23.在中, ,圆A的半径为1。若点0在BC上运动(与b,c点不重合),设OB=x,AOC面积为y.
(1).求y关于x的函数解析式,并写出函数的定义域
(2).以0为圆心,BO长为半径做圆0,当圆0与圆A相切时,求AOC的面积
例24.如图,圆A与圆B外切于点C,DE是两圆的一条外公切线,切点为d、E.
(1).判断的形状并证明
(2).过C作C0De于E,以直线DE为x轴,OC为y轴建立直角坐标系,且OE=2,OD=8.求过D、C、E三点的抛物线的解析式,并求出抛物线的顶点坐标
(3).该抛物线定点是否在连心线AB上?如果在,请证明,如果不在说明理由
例25.如图,在ABC中,AC=14,Bc=,=45.点O在AC上移动,圆O始终与AB相切。切点为D.圆O与AC相交于E、F(F可能在AC延长线上)
(1).设圆O半径为r,在满足题意的点O中是否存在某一位置,使得圆O与AB,BF都相切?若不存在,说明理由,若存在,求出此时r的长
(2).设四边形BDOC的面积为S.求S与r的函数关系式及r的取值范围
例26.如图,圆O与x轴交于A,B两点,与y轴交于C,D两点,圆心坐标为(1,-1),半径为
(1).比较线段AB与CD的大小。
(2).求A、B、C、D四点的坐标
(3).过D作圆的切线,求这条切线的解析式
三.几何综合题
1.线段的相等关系、比例关系的证明
例27.如图,MN切圆O于P,AB是圆O的弦,于M,BNMN于N,PQAB于Q
求证:PQ=
例28.如图,PA为圆O的切线,A为切点,PBC为割线,APC的平分线交AB于D,交AC于E
(1).求证:AD=AE
(2).求证:
例29.如图,BC是圆O的直径,ADBC于D,过B作弦BF交AD于E,交圆于F,交AC于H,且AE=BE
(2).
例30.如图,圆与圆相交于A、B两点,点在圆上,过A的直线交两圆于C、D.过B点的直线
交两圆于E、F.AB与相交于P
求证:(1).CE//DF
(2).
例31.如图,已知弦AB等于圆O的半径,连接OB并延长使BC=OB
(1).求证:AC是圆O的切线
(2).请在圆上取点D,使AD=AC(自己完成作图并给出证明过程)
例32.如图,两圆内切于点P,大圆的弦切小圆于C,PC的延长线交大圆于D
求证:(1).APD=BPD
(2).
例33.如图,内接于圆O,AB延长线与过C点的切线GC相交于点D,BE与AC相交于点F.且CB=CE.
求证:(1).BE//DG
(2)
2.几何的证明与计算题
例34.如图,PAB是圆O的割线,AB是圆O的直径,PC为圆O的切线,C为切点,BDPC于点D.交圆O于E.PA=AO=OB=1
(1).求P的度数。(2).求DE的长
例35.如图,圆O的内接ABC中,.AB=AC,D是圆O上一点,AD延长线交BC的延长线于P.
(1).求证:
(2).若圆O的直径为25,AB=20,AD=15,求PC和DC的长
例36..如图,PAQ是直角,半径为5的圆O与AP相切于点T.与AQ相交于点B、C.
(1).BT是否平分OBA 证明你的结论
(2).若已知At=4,求AB的长
例37.已知如图,圆O是ABC的外接圆,且AB=Ac=13,Bc=24.PA切圆O于a.割线PBD过圆心,交圆O于点B、D.连接CD
(1).求证:PA//Bc
(2).求圆O的半径及Cd的长。
例38.如图,梯形abcd中,AD//BC,AD=2,BC=4,对角线AC=5,Bd=3,试求该梯形的面积
6例39..如图,RTABC中,C=,以BC为直径的圆O交AB于点D,连接Od并延长交CA的延长线于点E.过D作DFOE交EC点于F.
(1).求证:AF=CF
(2).若eD=2,,求AD的长
例40.已知,如图,四边形AbcD内接于圆o,AB是圆o的直径,ce切圆o于e,aece.,交圆o于D
(1).求证:DC=BC.
(2).若DC:AB=3:5,求sinCAD的值
四.代数、几何综合题
1.圆与直线综合题
例41).如图,直线与x轴,y轴分别交于点A、B,OA=4,且OA,OB的长是关于x的方程的两个根。以OB为直径的圆M交AB于C.连接CM并延长交x轴于N
(1).求AB的解析式.
(2).求线段AC的长.
(3)求证:
(4).如果D是OA的中点,求证CD是圆M的切线
例42.如图,在直角坐标系中,以(a,0)为圆心的圆与x轴交于C、D两点,与y轴交于A、B两点。
连接AC
(1).点E在AB上,EA=EC,求证:
(2).在(1)的结论下,延长EC到P,连接PB,若PB=PE,试判断PB与圆的位置关系,并说明理由
(3).如果a=2,圆半径为4,求(2)中直线PB的解析式。
2.圆与方程综合
例43.如图,,PB=PM
求证:(1).是等边三角形
(2).PA,PB是关于x的方程的两根
例44..在中,AB=,AC=6,BC=,P是AC上与A、C不重合的一动点,过P、B、C的圆O交AB于D
(1).设,求y与x的函数关系式,并确定x的取值范围
(2).P在AC上何处时y有最小值?最小值是多少?
(3).求y取最小值时圆O的面积
例45.如图,两同心圆,大圆的弦AD交小圆于B、C,AE切小圆于E,连接CE,直线BE交大圆于P、Q.
已知BE=AE, AB=a,AE=b.
(1).求证:CD、CE的长是方程的两根
(2).求PB的长
例46.如图,以RtABC的直角顶点C为原点,以两条直角边AC.AB为x轴、y轴建立直角坐标系,圆O是ABC的内切圆,半径为r.两条直角边a、b是一元二次方程的两根。AB=c
(1).确定c与r的关系,c与m的关系
(2).当圆O面积为4时,求c和m的值
(3).求在(2)的条件下直线EF的解析式
2.圆与二次函数的综合题
例47.如图,抛物线交x轴的正方向于A、B亮点,交y轴的正方向于C点。经过A、B、C三点作圆O.若圆O与y轴相切
(1).求a、c满足的关系式
(2).设ACB=,求
(3).设抛物线顶点为P判断直线PA与圆O的位置关系
例48.如图,直线y=-x+1与两轴分别交于A、B两点,以AB为边长在第一象限内作正三角形ABC.圆为ABC的外接圆与x轴交于另一点E
(1).求C点坐标
(2).求过C点与AB中点的直线的解析式
(3).求过点E、、A三点的二次函数的解析式
例4.9如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4).与x轴相交于A、B两点,且AB=6
(1).求sinACB的值
(2)求经过C、A、B三点的抛物线的解析式
(3)设抛物线的顶点为F,判断直线FA与圆D的关系
例50.如图,AB是弦,CD是直径,ABCD于H,点P在DC延长线上,且PAH=POA,OH:HC=1:2,PC=6
(1).求证:PA是圆O的切线
(2).求圆O的半径的长
(3).试在弧ACB上取一点E(E与A、B不重合).并延长PE与弧ADB交于F,设FH=x,PF=y,求y与x之间的解析式,并指出x的取值范围。
第 1 页 共 16 页
同课章节目录
