2023-2024学年苏科版数学八年级上册 第3章勾股定理(用勾股定理解决面积问题)讲义(无答案)
文档属性
| 名称 | 2023-2024学年苏科版数学八年级上册 第3章勾股定理(用勾股定理解决面积问题)讲义(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 258.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 08:45:21 | ||
图片预览


文档简介
第3章勾股定理(用勾股定理解决面积问题)
【学习目标】
掌握利用勾股定理求三角形面积
掌握利用勾股定理求正方形面积
掌握利用勾股定理求稍复杂的勾股树问题
【典型例题】
类型一、利用勾股定理求三角形面积
【例1】已知如图,以的三边为斜边分别向外作等腰直角三角形,若斜边,则图中阴影部分的面积为_______.
举一反三:
【变式1】如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为 .
【变式2】如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连接BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
【变式3】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
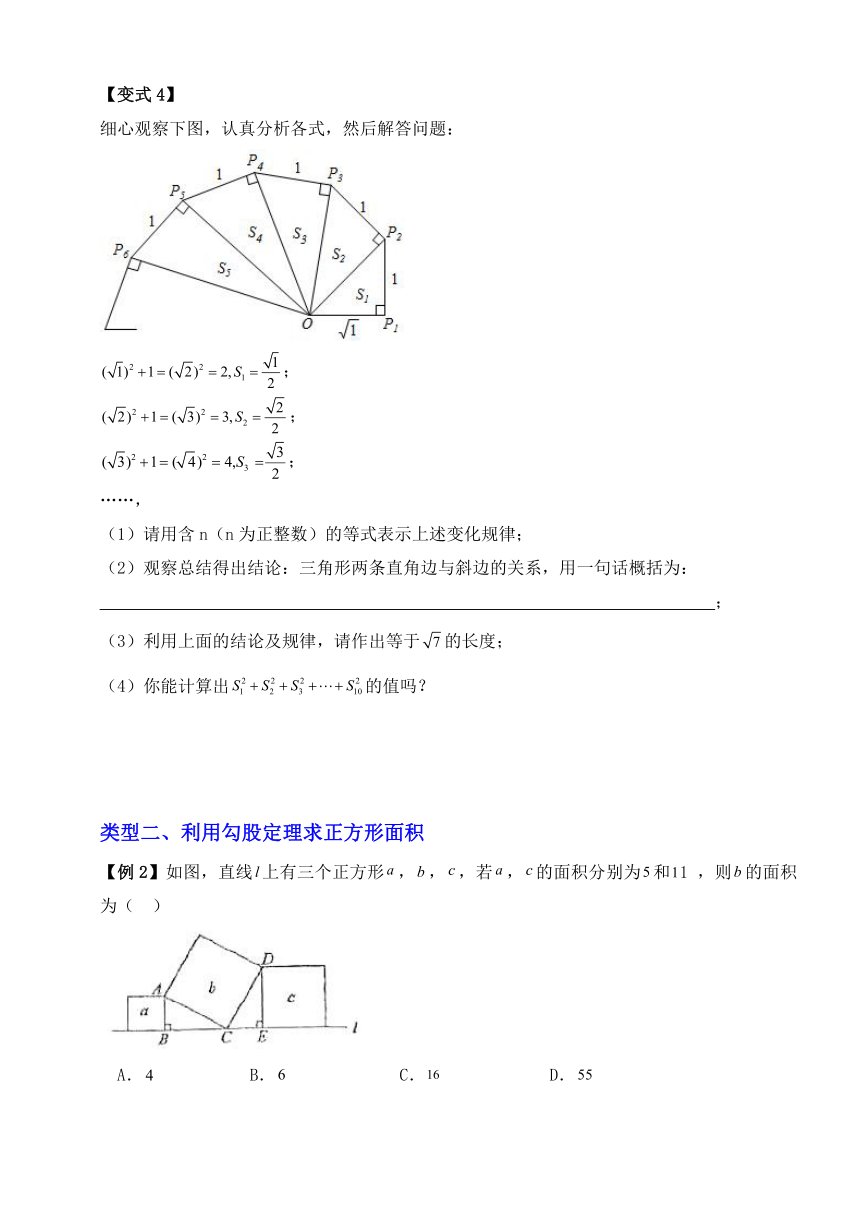
【变式4】
细心观察下图,认真分析各式,然后解答问题:
;
;
;
……,
(1)请用含n(n为正整数)的等式表示上述变化规律;
(2)观察总结得出结论:三角形两条直角边与斜边的关系,用一句话概括为:
;
(3)利用上面的结论及规律,请作出等于的长度;
(4)你能计算出的值吗?
类型二、利用勾股定理求正方形面积
【例2】如图,直线上有三个正方形,,,若,的面积分别为和1 ,则的面积为( )
A. B. C. D.
举一反三:
【变式1】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图, 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图 的方式放置在最大正方形内.若图中阴影部分的面积为,且 ,则 的长为( )
图1 图2
A. B. C. D.
【变式2】如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形,拼成如图2所示的“赵爽弦图”,得到大小两个正方形.
(1)用关于a的代数式表示图2中小正方形的边长;
(2)已知图2中小正方形面积为36,求大正方形的面积?
【变式3】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成. 将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为,,. 若, 则正方形EFGH的面积为_______.
【变式4】图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.
(1)在Rt△ABC中,AC=m,BC=n,∠ACB=90°,若图①中大正方形的面积为61,小正方形的面积为1,求(m+n)2;
(2)若将图①中的四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,求这个风车的外围周长(图中实线部分).
类型三、利用勾股定理求稍复杂的勾股树面积问题
【例3】如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
举一反三:
【变式1】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2022次后形成的图形中所有的正方形的面积和是( )
A.2022 B.2022 C.2022 D.2022
【变式2】如图,正方形的边长为2,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,…,按照此规律继续下去,则的值为___________.
【变式3】请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为____________(其中图 中出现的三角形均是直角三角形,四边形均是正方形).
【变式4】勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为,第二个正方形和第二个直角三角形的面积之和为,…,第个正方形和第个直角三角形的面积之和为.
设第一个正方形的边长为1.
请解答下列问题:
(1)______.
(2)通过探究,用含的代数式表示,则______.
【学习目标】
掌握利用勾股定理求三角形面积
掌握利用勾股定理求正方形面积
掌握利用勾股定理求稍复杂的勾股树问题
【典型例题】
类型一、利用勾股定理求三角形面积
【例1】已知如图,以的三边为斜边分别向外作等腰直角三角形,若斜边,则图中阴影部分的面积为_______.
举一反三:
【变式1】如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为 .
【变式2】如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连接BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
(1)求证:DF⊥AB;
(2)利用图中阴影部分面积完成勾股定理的证明,已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
【变式3】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法,证法如下:
把两个全等的直角三角形(Rt△ABC≌Rt△DAE)如图1放置,∠DAB=∠B=90°,AC⊥DE于点F,点E在边AB上,现设Rt△ACB两直角边长分别为CB=b、BA=a,斜边长为AC=c,请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理
(1)请根据上述图形的面积关系证明勾股定理;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,CD为两个村庄(看作直线上的两点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为多少千米.
【变式4】
细心观察下图,认真分析各式,然后解答问题:
;
;
;
……,
(1)请用含n(n为正整数)的等式表示上述变化规律;
(2)观察总结得出结论:三角形两条直角边与斜边的关系,用一句话概括为:
;
(3)利用上面的结论及规律,请作出等于的长度;
(4)你能计算出的值吗?
类型二、利用勾股定理求正方形面积
【例2】如图,直线上有三个正方形,,,若,的面积分别为和1 ,则的面积为( )
A. B. C. D.
举一反三:
【变式1】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图, 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图 的方式放置在最大正方形内.若图中阴影部分的面积为,且 ,则 的长为( )
图1 图2
A. B. C. D.
【变式2】如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形,拼成如图2所示的“赵爽弦图”,得到大小两个正方形.
(1)用关于a的代数式表示图2中小正方形的边长;
(2)已知图2中小正方形面积为36,求大正方形的面积?
【变式3】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成. 将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为,,. 若, 则正方形EFGH的面积为_______.
【变式4】图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.
(1)在Rt△ABC中,AC=m,BC=n,∠ACB=90°,若图①中大正方形的面积为61,小正方形的面积为1,求(m+n)2;
(2)若将图①中的四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,求这个风车的外围周长(图中实线部分).
类型三、利用勾股定理求稍复杂的勾股树面积问题
【例3】如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
举一反三:
【变式1】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2022次后形成的图形中所有的正方形的面积和是( )
A.2022 B.2022 C.2022 D.2022
【变式2】如图,正方形的边长为2,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,…,按照此规律继续下去,则的值为___________.
【变式3】请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为____________(其中图 中出现的三角形均是直角三角形,四边形均是正方形).
【变式4】勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为,第二个正方形和第二个直角三角形的面积之和为,…,第个正方形和第个直角三角形的面积之和为.
设第一个正方形的边长为1.
请解答下列问题:
(1)______.
(2)通过探究,用含的代数式表示,则______.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
