13.1轴对称 同步练习 (含答案) 2023—-2024学年人教版数学八年级上册
文档属性
| 名称 | 13.1轴对称 同步练习 (含答案) 2023—-2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 270.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 00:00:00 | ||
图片预览

文档简介
13.1轴对称 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列轴对称图形中,对称轴条数最少的是( )
A.等边三角形 B.正方形 C.正六边形 D.圆
2.下列图形中,不是轴对称图形的是( )
A. B. C. D.
3.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2 B.4 C.6 D.8
4.已知:如图,,点P在的内部,,点与点P关于对称,点与点P关于对称,那么以、O、三点为顶点的三角形面积是( )
A.4 B.8 C.16 D.无法确定
5.如图,锐角按下列步骤作图:①在射线OA上取一点,以点O为圆心,OC长为半径作圆弧DE,交射线OB于点F,连接;②以点F为圆心,CF长为半径作圆弧,交弧DE于点;③连接FG、CG,作射线OG.根据以上作图过程及所作图形,下列结论中错误的是( )
A.OG=OC B. C.OF垂直平分CG D.OC=2FG
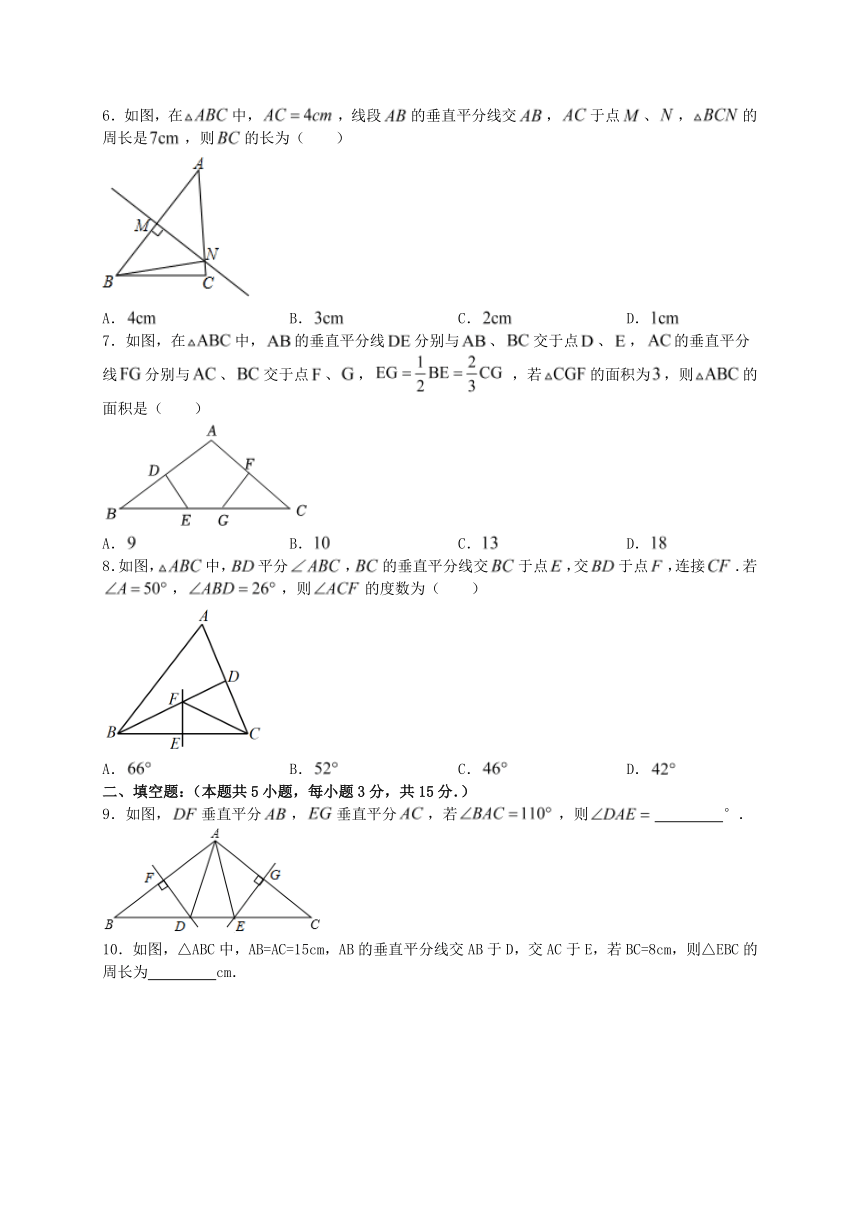
6.如图,在中,,线段的垂直平分线交,于点、,的周长是,则的长为( )
A. B. C. D.
7.如图,在中,的垂直平分线分别与、交于点、,的垂直平分线分别与、交于点、,,若的面积为,则的面积是( )
A. B. C. D.
8.如图,中,平分,的垂直平分线交于点,交于点,连接.若,,则的度数为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.如图,垂直平分,垂直平分,若,则 °.
10.如图,△ABC中,AB=AC=15cm,AB的垂直平分线交AB于D,交AC于E,若BC=8cm,则△EBC的周长为 cm.
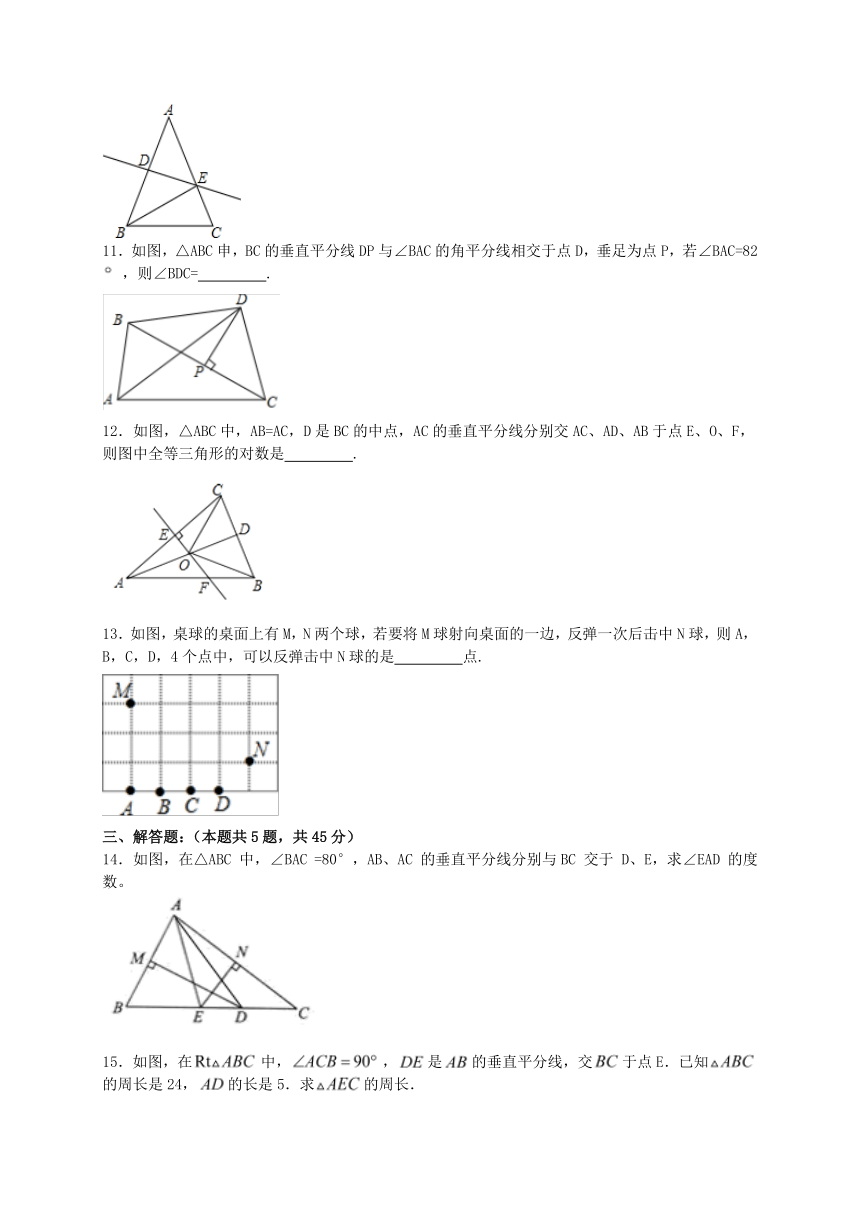
11.如图,△ABC申,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=82 ,则∠BDC= .
12.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是 .
13.如图,桌球的桌面上有M,N两个球,若要将M球射向桌面的一边,反弹一次后击中N球,则A,B,C,D,4个点中,可以反弹击中N球的是 点.
三、解答题:(本题共5题,共45分)
14.如图,在△ABC 中,∠BAC =80°,AB、AC 的垂直平分线分别与BC 交于 D、E,求∠EAD 的度数。
15.如图,在中,,是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
16.如图,ABC的边BC的垂直平分线DE交ABC的外角平分线AD于点D,DF⊥AB于点F,且AB>AC,试探究BF、AC、AF之间的数量关系,并说明理由.
17.如图,在中,,垂足为D,,垂足为E,,与相交于点F.
(1)请说明的理由.
(2)如果,说明的理由.
18.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
参考答案:
1.A 2.C 3.C 4.B 5.D 6.B 7.D 8.B
9.
10.23
11.
12.4
13.D
14.解:∵ AB,AC的垂直平分线MD和EN分别与BC交于D,E
∴ DA=DB,AE=CE,
∴∠ABD=∠BAD,∠EAC=∠ECA,
∴∠BAD+∠EAC=∠ABD+∠ECA=180°-∠BAC=100°,
又∵∠BAD+∠EAC=∠ BAE+∠EAD+∠DAC+∠EAD=∠BAC+∠EAD=80°+∠EAD=100°,
∴∠EAD=100°-80°=20°,
15.解:∵是的垂直平分线,
∴,,
∵,
∴,
∵的周长为24,
∴,
∵
∴的周长为14.
16.解: ,理由如下:
如图,过点D作DG⊥CA,交CA的延长线于点G,连接 , ,
平分 , , ,
, ,
垂直平分 ,
,
在 和 中,
,
∴ ,
,
在 和 中,
,
∴ ,
.
,
∴ .
17.(1)证明:∵,,
∴,
又,,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
又,
∴垂直平分,
∴.
18.(1)证明:∵BD=DE,AD⊥BC,
∴AD垂直平分BE,
∴AB=AE,
∴∠B=∠AEB;
∵∠B+∠AEB+∠BAE=180°,∠BAE=40°,
∴∠B=∠AEB=70°;
∵EF垂直平分AC,
∴AE=EC,
∴∠EAC=∠C
∵∠AEB=∠C+∠EAC,
∴∠C=∠AEB=35°.
(2)解:
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.下列轴对称图形中,对称轴条数最少的是( )
A.等边三角形 B.正方形 C.正六边形 D.圆
2.下列图形中,不是轴对称图形的是( )
A. B. C. D.
3.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2 B.4 C.6 D.8
4.已知:如图,,点P在的内部,,点与点P关于对称,点与点P关于对称,那么以、O、三点为顶点的三角形面积是( )
A.4 B.8 C.16 D.无法确定
5.如图,锐角按下列步骤作图:①在射线OA上取一点,以点O为圆心,OC长为半径作圆弧DE,交射线OB于点F,连接;②以点F为圆心,CF长为半径作圆弧,交弧DE于点;③连接FG、CG,作射线OG.根据以上作图过程及所作图形,下列结论中错误的是( )
A.OG=OC B. C.OF垂直平分CG D.OC=2FG
6.如图,在中,,线段的垂直平分线交,于点、,的周长是,则的长为( )
A. B. C. D.
7.如图,在中,的垂直平分线分别与、交于点、,的垂直平分线分别与、交于点、,,若的面积为,则的面积是( )
A. B. C. D.
8.如图,中,平分,的垂直平分线交于点,交于点,连接.若,,则的度数为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.如图,垂直平分,垂直平分,若,则 °.
10.如图,△ABC中,AB=AC=15cm,AB的垂直平分线交AB于D,交AC于E,若BC=8cm,则△EBC的周长为 cm.
11.如图,△ABC申,BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=82 ,则∠BDC= .
12.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是 .
13.如图,桌球的桌面上有M,N两个球,若要将M球射向桌面的一边,反弹一次后击中N球,则A,B,C,D,4个点中,可以反弹击中N球的是 点.
三、解答题:(本题共5题,共45分)
14.如图,在△ABC 中,∠BAC =80°,AB、AC 的垂直平分线分别与BC 交于 D、E,求∠EAD 的度数。
15.如图,在中,,是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
16.如图,ABC的边BC的垂直平分线DE交ABC的外角平分线AD于点D,DF⊥AB于点F,且AB>AC,试探究BF、AC、AF之间的数量关系,并说明理由.
17.如图,在中,,垂足为D,,垂足为E,,与相交于点F.
(1)请说明的理由.
(2)如果,说明的理由.
18.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
参考答案:
1.A 2.C 3.C 4.B 5.D 6.B 7.D 8.B
9.
10.23
11.
12.4
13.D
14.解:∵ AB,AC的垂直平分线MD和EN分别与BC交于D,E
∴ DA=DB,AE=CE,
∴∠ABD=∠BAD,∠EAC=∠ECA,
∴∠BAD+∠EAC=∠ABD+∠ECA=180°-∠BAC=100°,
又∵∠BAD+∠EAC=∠ BAE+∠EAD+∠DAC+∠EAD=∠BAC+∠EAD=80°+∠EAD=100°,
∴∠EAD=100°-80°=20°,
15.解:∵是的垂直平分线,
∴,,
∵,
∴,
∵的周长为24,
∴,
∵
∴的周长为14.
16.解: ,理由如下:
如图,过点D作DG⊥CA,交CA的延长线于点G,连接 , ,
平分 , , ,
, ,
垂直平分 ,
,
在 和 中,
,
∴ ,
,
在 和 中,
,
∴ ,
.
,
∴ .
17.(1)证明:∵,,
∴,
又,,
∴;
(2)解:∵,
∴,
∵,
∴,
∴,
又,
∴垂直平分,
∴.
18.(1)证明:∵BD=DE,AD⊥BC,
∴AD垂直平分BE,
∴AB=AE,
∴∠B=∠AEB;
∵∠B+∠AEB+∠BAE=180°,∠BAE=40°,
∴∠B=∠AEB=70°;
∵EF垂直平分AC,
∴AE=EC,
∴∠EAC=∠C
∵∠AEB=∠C+∠EAC,
∴∠C=∠AEB=35°.
(2)解:
