1.3 相似三角形的性质 同步练习(有答案) 2023—2024学年青岛版数学九年级上册
文档属性
| 名称 | 1.3 相似三角形的性质 同步练习(有答案) 2023—2024学年青岛版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 141.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 10:44:48 | ||
图片预览



文档简介
2023年青岛版数学九年级上册
《1.3 相似三角形的性质》同步练习
一 、选择题
1.已知△ABC∽△DEF,若△ABC与△DEF的面积比为4:9,则△ABC与△DEF的周长比为( )
A.16:81 B.4:9 C.3:2 D.2:3
2.如图,DE∥BC,分别交△ABC的边AB,AC于点D,E,=,若AE=5,则EC长度为( )
A.10 B.15 C.20 D.25
3.如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
A.5.5 B.5.25 C.6.5 D.7
4.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠BAC度数为( )
A.135° B.125° C.115° D. 105°
5.两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
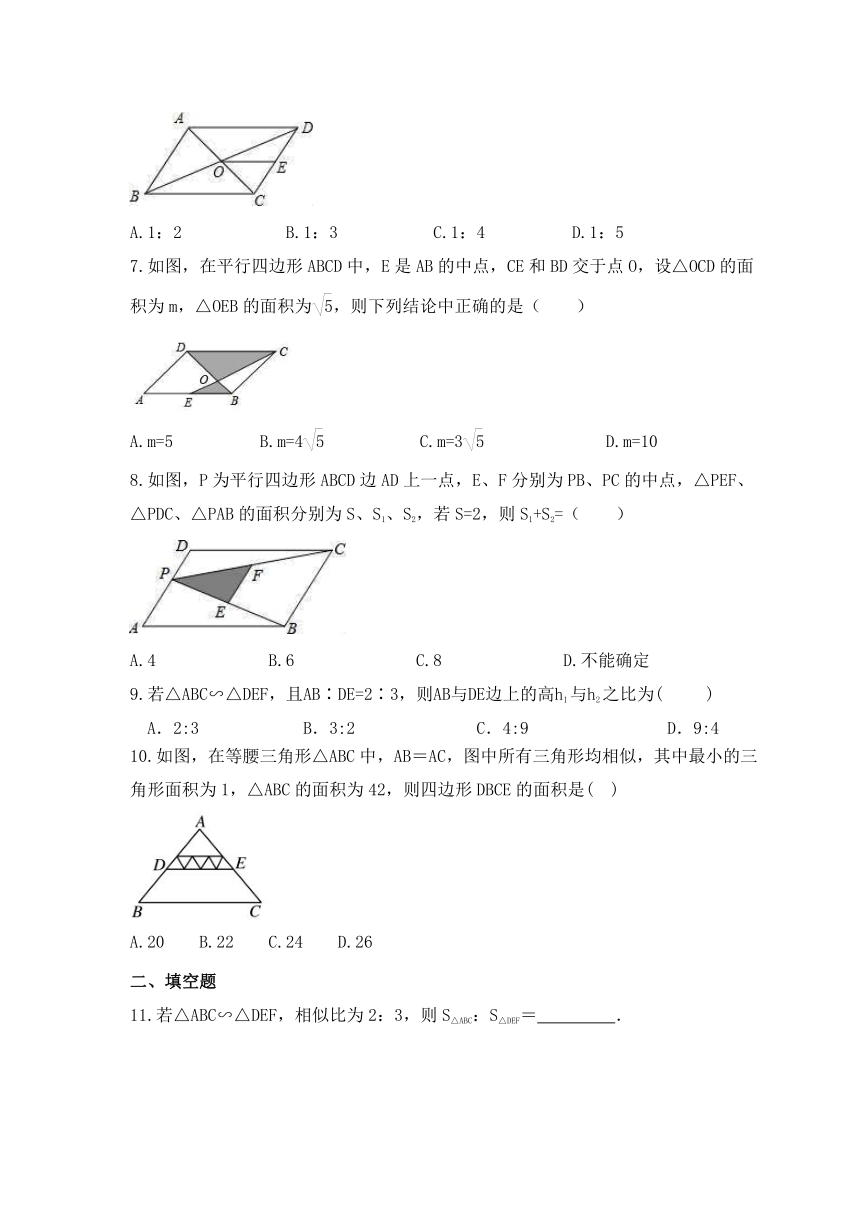
6.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
7.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m=4 C.m=3 D.m=10
8.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )
A.4 B.6 C.8 D.不能确定
9.若△ABC∽△DEF,且AB∶DE=2∶3,则AB与DE边上的高h1与h2之比为( )
A.2:3 B.3:2 C.4:9 D.9:4
10.如图,在等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为42,则四边形DBCE的面积是( )
A.20 B.22 C.24 D.26
二 、填空题
11.若△ABC∽△DEF,相似比为2:3,则S△ABC:S△DEF= .
12.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE= .
13.若△ABC∽△A′B′C′,且AB:A′B′=3:4,△ABC的周长为12 cm,则△A′B′C′的周长为____________.
14.两个相似三角形面积比是9:25,其中较小一个三角形的周长为18cm,则另一个三角形的周长是 cm.
15.如图,在Rt△ABC中,∠ACB=90°,直线EF∥BD交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则=____.
16.如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为 .
三 、解答题
17.如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
18.如图,在△ABC 中,D,E 分别是边 AB,AC 上的点,连接 DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)如果 E 是 AC 的中点,AD=8,AB=10,求 AE 的长.
19.为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
20.一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度,如图,当李明走到点A处时,张龙测得李明直立身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m.已知李明直立时的身高为1.75m,求路灯CD的高.
21.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图①,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1) 求证:△AEF∽△ABC;
(2) 求这个正方形零件的边长;
(3) 如果把它加工成矩形零件如图②,问这个矩形的最大面积是多少?
答案
1.D
2.A
3.B.
4.B
5.A
6.A.
7.B.
8.C.
9.A
10.D.
11.答案为:4:9.
12.答案为:1:3.
13.答案为:16cm.
14.答案为:30.
15.答案为:.
16.答案为:()2022.
17.解:(1)∵AB=AC,AD为BC边上的中线,
∴AD⊥BC,∠B=∠C.
∵DE⊥AB,∴∠DEB=∠ADC=90°,
∴△BDE∽△CAD;
(2)由(1)知,∠ADB=90°.
在Rt△ADB中,BD=BC=5,
∴AD===12.
∵S△ABD=AD·BD=AB·DE,
∴DE=.
18.解:(1)∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB;
(2)由(1)可知:△ADE∽△ACB,
∴ = ,
∵点 E 是 AC 的中点,
设 AE=x,
∴AC=2AE=2x,
∵AD=8,AB=10,
∴ = ,解得:x=2 ,
∴AE=2 .
19.解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得=(米).
答:两岸间的大致距离为100米.
20.解:由题意知AM=BN=1.75m,设CD=xm.
∵AE=AM,AM⊥EC,
∴∠E=45°,
∴EC=CD=xm,AC=(x-1.75)m.
∵CD⊥EC,BN⊥EC,
∴BN∥CD,
∴△ABN∽△ACD,
解得x=6.125.
答:路灯CD的高为6.125m.
21.解:(1)∵四边形EFHG为正方形,
∴BC∥EF,
∴△AEF∽△ABC
(2)∵四边形EFHG为正方形,
∴EF∥BC,EG⊥BC,
又∵AD⊥BC,
∴EG∥AD,
设EG=EF=x,则KD=x,
∵BC=120 mm,AD=80 mm,
∴AK=80-x,
∵△AEF∽△ABC,
∴=,即=,解得x=48,
∴这个正方形零件的边长是48 mm
(3)设EG=KD=m,则AK=80-m,
∵△AEF∽△ABC,
∴=,即=,
∴EF=120-m,
∴S矩形EFHG=EG·EF=m·(120-m)=-m2+120m=-(m-40)2+2400,
故当m=40时,矩形EFHG的面积最大,最大面积为2400 mm2
《1.3 相似三角形的性质》同步练习
一 、选择题
1.已知△ABC∽△DEF,若△ABC与△DEF的面积比为4:9,则△ABC与△DEF的周长比为( )
A.16:81 B.4:9 C.3:2 D.2:3
2.如图,DE∥BC,分别交△ABC的边AB,AC于点D,E,=,若AE=5,则EC长度为( )
A.10 B.15 C.20 D.25
3.如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
A.5.5 B.5.25 C.6.5 D.7
4.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠BAC度数为( )
A.135° B.125° C.115° D. 105°
5.两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
6.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
7.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m=4 C.m=3 D.m=10
8.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )
A.4 B.6 C.8 D.不能确定
9.若△ABC∽△DEF,且AB∶DE=2∶3,则AB与DE边上的高h1与h2之比为( )
A.2:3 B.3:2 C.4:9 D.9:4
10.如图,在等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为42,则四边形DBCE的面积是( )
A.20 B.22 C.24 D.26
二 、填空题
11.若△ABC∽△DEF,相似比为2:3,则S△ABC:S△DEF= .
12.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE= .
13.若△ABC∽△A′B′C′,且AB:A′B′=3:4,△ABC的周长为12 cm,则△A′B′C′的周长为____________.
14.两个相似三角形面积比是9:25,其中较小一个三角形的周长为18cm,则另一个三角形的周长是 cm.
15.如图,在Rt△ABC中,∠ACB=90°,直线EF∥BD交AB于点E,交AC于点G,交AD于点F.若S△AEG=S四边形EBCG,则=____.
16.如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为 .
三 、解答题
17.如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
18.如图,在△ABC 中,D,E 分别是边 AB,AC 上的点,连接 DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)如果 E 是 AC 的中点,AD=8,AB=10,求 AE 的长.
19.为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.
20.一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度,如图,当李明走到点A处时,张龙测得李明直立身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m.已知李明直立时的身高为1.75m,求路灯CD的高.
21.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图①,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1) 求证:△AEF∽△ABC;
(2) 求这个正方形零件的边长;
(3) 如果把它加工成矩形零件如图②,问这个矩形的最大面积是多少?
答案
1.D
2.A
3.B.
4.B
5.A
6.A.
7.B.
8.C.
9.A
10.D.
11.答案为:4:9.
12.答案为:1:3.
13.答案为:16cm.
14.答案为:30.
15.答案为:.
16.答案为:()2022.
17.解:(1)∵AB=AC,AD为BC边上的中线,
∴AD⊥BC,∠B=∠C.
∵DE⊥AB,∴∠DEB=∠ADC=90°,
∴△BDE∽△CAD;
(2)由(1)知,∠ADB=90°.
在Rt△ADB中,BD=BC=5,
∴AD===12.
∵S△ABD=AD·BD=AB·DE,
∴DE=.
18.解:(1)∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB;
(2)由(1)可知:△ADE∽△ACB,
∴ = ,
∵点 E 是 AC 的中点,
设 AE=x,
∴AC=2AE=2x,
∵AD=8,AB=10,
∴ = ,解得:x=2 ,
∴AE=2 .
19.解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,
∴△ABD∽△ECD,
∴,,
解得=(米).
答:两岸间的大致距离为100米.
20.解:由题意知AM=BN=1.75m,设CD=xm.
∵AE=AM,AM⊥EC,
∴∠E=45°,
∴EC=CD=xm,AC=(x-1.75)m.
∵CD⊥EC,BN⊥EC,
∴BN∥CD,
∴△ABN∽△ACD,
解得x=6.125.
答:路灯CD的高为6.125m.
21.解:(1)∵四边形EFHG为正方形,
∴BC∥EF,
∴△AEF∽△ABC
(2)∵四边形EFHG为正方形,
∴EF∥BC,EG⊥BC,
又∵AD⊥BC,
∴EG∥AD,
设EG=EF=x,则KD=x,
∵BC=120 mm,AD=80 mm,
∴AK=80-x,
∵△AEF∽△ABC,
∴=,即=,解得x=48,
∴这个正方形零件的边长是48 mm
(3)设EG=KD=m,则AK=80-m,
∵△AEF∽△ABC,
∴=,即=,
∴EF=120-m,
∴S矩形EFHG=EG·EF=m·(120-m)=-m2+120m=-(m-40)2+2400,
故当m=40时,矩形EFHG的面积最大,最大面积为2400 mm2
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
