2.5.1 直线与圆的位置关系(第1课时) 课件(共21张PPT)
文档属性
| 名称 | 2.5.1 直线与圆的位置关系(第1课时) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 46.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 22:13:45 | ||
图片预览







文档简介
(共21张PPT)
2.5.1 直线与圆的位置关系
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1.理解直线和圆的三种位置关系.
2.会用圆心到直线的距离来判断直线与圆的位置关系.
3.会用代数法来判断直线与圆的位置关系
4.能解决直线与圆位置关系的求切线方程、求弦长等综合问题.
情景导入
“海上生明月,天涯共此时。”,表达了诗人望月怀人的深厚情谊。在海天交于一线的天际,一轮明月慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着迷人的风采.
这个过程中,月亮看作一个圆,海天交线看作一条直线,月出的过程中也体现了直线与圆的三种位置关系:相交、相切和相离.
在平面几何中,我们研究过直线与圆这两类图形的位置关系,前面我们学习了直线的方程,圆的方程,已经用方程研究两条直线的位置关系,下面我们类比用方程研究两条直线位置关系的方法,利用直线和圆的方程通过定量计算研究直线与圆的位置关系。
直线与圆的位置关系
探究1:怎样用几何法即用圆心到直线的距离d同圆的半径r的大小关系来判断直线与圆的位置关系?
提示:利用圆心到直线的距离d与圆半径r的大小关系判断它们之间的位置关系如下:
若d>r,则直线与圆相离;若d=r,则直线与圆相切;若d直线与圆的位置关系
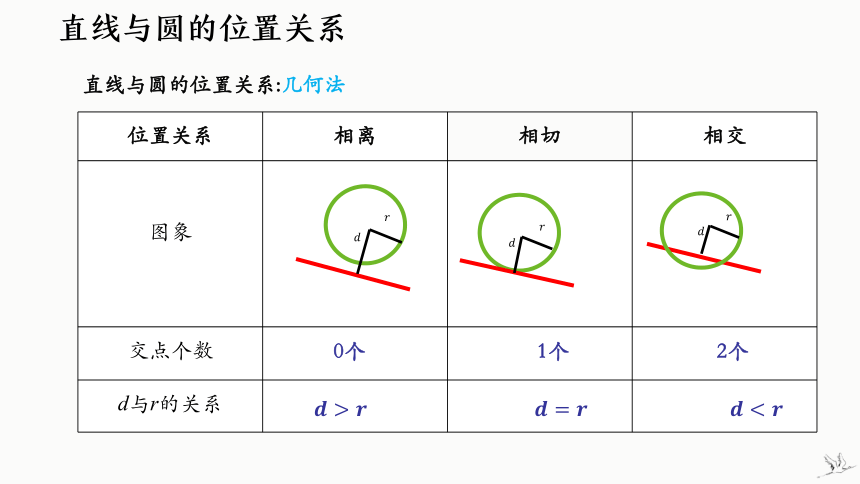
直线与圆的位置关系:几何法
位置关系 相离 相切 相交
图象
交点个数
d与r的关系
0个
1个
2个
直线与圆的位置关系
探究2:直线l:Ax+By+C=0(A,B不同时为0),圆C:(x-a)2+(y-b)2=r2(r>0),如何用直线和圆的方程判断它们之间的位置关系?
提示:联立直线l和圆C的方程得方程组,
联立方程组消去x(或y)得一元二次方程。当方程组无解即Δ<0时,直线与圆相离;方程组有一解即Δ=0时,直线与圆相切;方程组有两解即Δ>0时,直线与圆相交.
直线与圆的位置关系
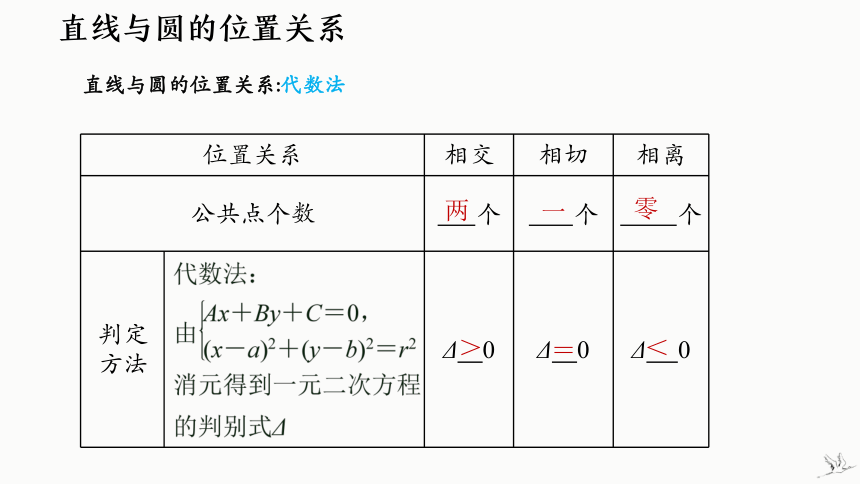
位置关系 相交 相切 相离
公共点个数 个 个 个
判定 方法 Δ 0 Δ 0 Δ 0
>
=
<
两
一
零
直线与圆的位置关系:代数法
直线与圆的位置关系
1.直线3x+4y=5与圆x2+y2=16的位置关系是( )
A.相交 B.相切 C.相离 D.相切或相交
A
2.直线y=x+1与圆x2+y2=1的位置关系是( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
B
直线与圆的位置关系
例1:已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求出它们交点的坐标.
解:方法一:由直线与圆的方程得方程组
消去y,得x2-3x+2=0.
∵Δ=(-3)2-4×1×2=1>0,
∴直线与圆相交,有两个交点.
由方程组解得交点坐标为(2,0),(1,3).
直线与圆的位置关系
解:方法二:圆的方程可化为x2+(y-1)2=5,其圆心为(0,1),半径为.圆心到直线l的距离为d,
∴直线与圆相交,有两个交点.
由直线与圆的方程得方程组
解得交点坐标为(2,0),(1,3).
直线与圆的位置关系
例2 已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点
分析:法一可联立方程组,由方程组解的个数判断,
法二也可求出圆心到直线的距离,通过与半径比较大小判断.
直线与圆的位置关系
解:(方法1)将直线mx-y-m-1=0代入圆的方程,
得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
直线与圆的位置关系
直线与圆的位置关系
直线与圆的位置关系的判断方法
直线与圆的位置关系反映在三个方面:
一是点到直线的距离与半径大小的关系;
二是直线与圆的公共点的个数;
三是两方程组成的方程组解的个数.
因此,若给出图形,可根据公共点的个数判断;若给出直线与圆的方程,可选择用几何法或代数法,几何法计算量小,代数法可一同求出交点.解题时可根据条件作出恰当的选择.
圆的弦长
求直线与圆相交时弦长的两种方法:
(1)几何法:如图1,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有+d2=r2.即|AB|=2 .一般地出现直线与圆相交的弦长问题常用几何法.
(2)代数法:如图2所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),则|AB|=,其中k为直线l的斜率.此代数法运算较麻烦.
圆的弦长
例1. 求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长.
解:法一:由得交点A(1,3),B(2,0),
∴弦AB的长为|AB|== .
法二:圆C:x2+y2-2y-4=0可化为x2+(y-1)2=5,其圆心坐标(0,1),半径r=,点(0,1)到直线l的距离为d==,所以半弦长为 ===,所以弦长|AB|=.
圆的弦长
练习.若过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为4,
则直线l的方程为________.
解:将圆的方程写成标准形式,得x2+(y+2)2=25.
①直线l斜率不存在,则直线方程为x=-3.圆心到该直线距离为3,又圆半径为5,所以求得弦长为8,不合题意,舍去.
②直线l的斜率存在,设直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.
圆心到直线l的距离为d=,
则+(2)2=25.解得k=- 或k=2.
所求直线的方程为y+3=-(x+3)或y+3=2(x+3),即x+2y+9=0或2x-y+3=0.
圆的切线
切线方程的求法
1.求过圆上一点P(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,则由垂直关系,切线斜率为- ,由点斜式方程可求得切线方程.若k=0或斜率不存在,则由图形可直接得切线方程为y=b或x=a.
2.求过圆外一点P(x0,y0)的圆的切线时,常用几何方法求解
设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0,由圆心到直线的距离等于半径,可求得k,进而切线方程即可求出.但要注意,此时的切线有两条,若求出的k值只有一个时,则另一条切线的斜率一定不存在,可通过数形结合求出.
圆的切线
例2.若直线l过点P(2,3),且与圆(x-1)2+(y+2)2=1相切,求直线l的方程.
【解析】∵(2-1)2+(3+2)2>1,∴点P在圆外.
法一:①若直线l的斜率存在,设l:y-3=k(x-2),
即kx-y+3-2k=0,因为直线l与圆(x-1)2+(y+2)2=1相切,所以 =1,所以k=.
所以直线l的方程为y-3= (x-2),
即12x-5y-9=0.
②若直线l的斜率不存在,则直线l:x=2也符合要求.
所以直线l的方程为12x-5y-9=0或x=2.
圆的切线
练习: 过点Q(3,0)作圆x2+y2=4的切线,求此切线方程.
课堂小结
2.5.1 直线与圆的位置关系
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1.理解直线和圆的三种位置关系.
2.会用圆心到直线的距离来判断直线与圆的位置关系.
3.会用代数法来判断直线与圆的位置关系
4.能解决直线与圆位置关系的求切线方程、求弦长等综合问题.
情景导入
“海上生明月,天涯共此时。”,表达了诗人望月怀人的深厚情谊。在海天交于一线的天际,一轮明月慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着迷人的风采.
这个过程中,月亮看作一个圆,海天交线看作一条直线,月出的过程中也体现了直线与圆的三种位置关系:相交、相切和相离.
在平面几何中,我们研究过直线与圆这两类图形的位置关系,前面我们学习了直线的方程,圆的方程,已经用方程研究两条直线的位置关系,下面我们类比用方程研究两条直线位置关系的方法,利用直线和圆的方程通过定量计算研究直线与圆的位置关系。
直线与圆的位置关系
探究1:怎样用几何法即用圆心到直线的距离d同圆的半径r的大小关系来判断直线与圆的位置关系?
提示:利用圆心到直线的距离d与圆半径r的大小关系判断它们之间的位置关系如下:
若d>r,则直线与圆相离;若d=r,则直线与圆相切;若d
直线与圆的位置关系:几何法
位置关系 相离 相切 相交
图象
交点个数
d与r的关系
0个
1个
2个
直线与圆的位置关系
探究2:直线l:Ax+By+C=0(A,B不同时为0),圆C:(x-a)2+(y-b)2=r2(r>0),如何用直线和圆的方程判断它们之间的位置关系?
提示:联立直线l和圆C的方程得方程组,
联立方程组消去x(或y)得一元二次方程。当方程组无解即Δ<0时,直线与圆相离;方程组有一解即Δ=0时,直线与圆相切;方程组有两解即Δ>0时,直线与圆相交.
直线与圆的位置关系
位置关系 相交 相切 相离
公共点个数 个 个 个
判定 方法 Δ 0 Δ 0 Δ 0
>
=
<
两
一
零
直线与圆的位置关系:代数法
直线与圆的位置关系
1.直线3x+4y=5与圆x2+y2=16的位置关系是( )
A.相交 B.相切 C.相离 D.相切或相交
A
2.直线y=x+1与圆x2+y2=1的位置关系是( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
B
直线与圆的位置关系
例1:已知直线l:3x+y-6=0和圆C:x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求出它们交点的坐标.
解:方法一:由直线与圆的方程得方程组
消去y,得x2-3x+2=0.
∵Δ=(-3)2-4×1×2=1>0,
∴直线与圆相交,有两个交点.
由方程组解得交点坐标为(2,0),(1,3).
直线与圆的位置关系
解:方法二:圆的方程可化为x2+(y-1)2=5,其圆心为(0,1),半径为.圆心到直线l的距离为d,
∴直线与圆相交,有两个交点.
由直线与圆的方程得方程组
解得交点坐标为(2,0),(1,3).
直线与圆的位置关系
例2 已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,直线与圆
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点
分析:法一可联立方程组,由方程组解的个数判断,
法二也可求出圆心到直线的距离,通过与半径比较大小判断.
直线与圆的位置关系
解:(方法1)将直线mx-y-m-1=0代入圆的方程,
得(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
直线与圆的位置关系
直线与圆的位置关系
直线与圆的位置关系的判断方法
直线与圆的位置关系反映在三个方面:
一是点到直线的距离与半径大小的关系;
二是直线与圆的公共点的个数;
三是两方程组成的方程组解的个数.
因此,若给出图形,可根据公共点的个数判断;若给出直线与圆的方程,可选择用几何法或代数法,几何法计算量小,代数法可一同求出交点.解题时可根据条件作出恰当的选择.
圆的弦长
求直线与圆相交时弦长的两种方法:
(1)几何法:如图1,直线l与圆C交于A,B两点,设弦心距为d,圆的半径为r,弦长为|AB|,则有+d2=r2.即|AB|=2 .一般地出现直线与圆相交的弦长问题常用几何法.
(2)代数法:如图2所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A(x1,y1),B(x2,y2),则|AB|=,其中k为直线l的斜率.此代数法运算较麻烦.
圆的弦长
例1. 求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长.
解:法一:由得交点A(1,3),B(2,0),
∴弦AB的长为|AB|== .
法二:圆C:x2+y2-2y-4=0可化为x2+(y-1)2=5,其圆心坐标(0,1),半径r=,点(0,1)到直线l的距离为d==,所以半弦长为 ===,所以弦长|AB|=.
圆的弦长
练习.若过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为4,
则直线l的方程为________.
解:将圆的方程写成标准形式,得x2+(y+2)2=25.
①直线l斜率不存在,则直线方程为x=-3.圆心到该直线距离为3,又圆半径为5,所以求得弦长为8,不合题意,舍去.
②直线l的斜率存在,设直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.
圆心到直线l的距离为d=,
则+(2)2=25.解得k=- 或k=2.
所求直线的方程为y+3=-(x+3)或y+3=2(x+3),即x+2y+9=0或2x-y+3=0.
圆的切线
切线方程的求法
1.求过圆上一点P(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,则由垂直关系,切线斜率为- ,由点斜式方程可求得切线方程.若k=0或斜率不存在,则由图形可直接得切线方程为y=b或x=a.
2.求过圆外一点P(x0,y0)的圆的切线时,常用几何方法求解
设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0,由圆心到直线的距离等于半径,可求得k,进而切线方程即可求出.但要注意,此时的切线有两条,若求出的k值只有一个时,则另一条切线的斜率一定不存在,可通过数形结合求出.
圆的切线
例2.若直线l过点P(2,3),且与圆(x-1)2+(y+2)2=1相切,求直线l的方程.
【解析】∵(2-1)2+(3+2)2>1,∴点P在圆外.
法一:①若直线l的斜率存在,设l:y-3=k(x-2),
即kx-y+3-2k=0,因为直线l与圆(x-1)2+(y+2)2=1相切,所以 =1,所以k=.
所以直线l的方程为y-3= (x-2),
即12x-5y-9=0.
②若直线l的斜率不存在,则直线l:x=2也符合要求.
所以直线l的方程为12x-5y-9=0或x=2.
圆的切线
练习: 过点Q(3,0)作圆x2+y2=4的切线,求此切线方程.
课堂小结
