4.3角(共20张PPT) 2023-2024学年人教版数学七年级上学期
文档属性
| 名称 | 4.3角(共20张PPT) 2023-2024学年人教版数学七年级上学期 |

|
|
| 格式 | pptx | ||
| 文件大小 | 895.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
角
第四章 几何图形初步
角的定义
你能归纳出角的特点吗?用自己的话描述一下角是由什么组成的图形?
观察与思考
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
角的有关概念
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
始边
终边
O
A
B
(B)
平角
周角
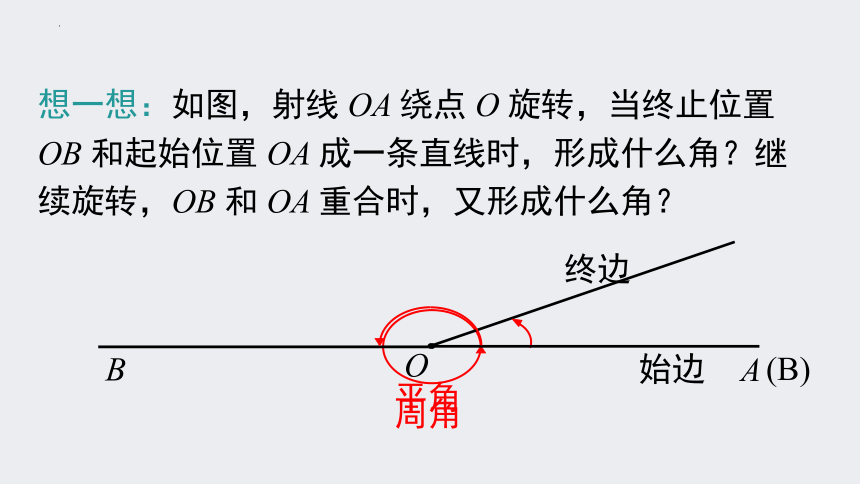
想一想:如图,射线 OA 绕点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
说明:
在不做特别说明的情况下,我们说的角都指不大于平角的角
判断题:
(1)两条射线组成的图形叫角。
(2)角的大小与边的长短无关。
(3)角的 两边是两条射线。
A
B
C
.
.
.
1.角通常用三个大写字母及符号“∠”表示.三个大写字母应分别是顶点和两边上的任意点,顶点的字母必须写在中间.
角的表示
O
A
B
记作:
∠AOB
或
∠BOA
注意:顶点字母写在中间.
2.角也可用一个大写字母来表示,这个字母是表示顶点的大写字母,但当两个或两个以上的角有同一个顶点时,不能用一个大写字母表示.
O
∠O
记作:
条件:顶点处只有一个角.
3.角还可用一个数字或一个希腊字母表示,在角的内部靠近角的顶点处画一弧线,写上数字或希腊字母.
1
记作:∠1
有以新的方式出现的角吗
归纳:角也可以看成是由一条射线绕着它的端点旋转而形成的图形.
1. 图中有 个角,你能把它们表示出来吗?
3
练一练
A
E
C
O
∠AOE,∠COE,∠AOC.
2. 填写下表,将图中的角用不同方法表示出来.
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
角的度量
角的度量工具:
量角器
怎么知道这个角的大小?
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是 1 度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
A
O
B
如图,已知∠AOB,画∠EOF = ∠AOB,你有什么方法?
300
18000
38
9
0.6
0.01
38.25
5°= ′= ″;38.15°= ° ′;36″= ′= °;
38°15′= °.
练一练
例 如图,时钟显示为10:10时,时针与分针所夹
角度是 ( )
A.90° B.100° C.105° D.115°
解析:时针每小时旋转的夹角360°
÷12=30°,故10分钟,时针旋转的角度为5°,即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
练习
从蜂巢的入口处看,蜂巢由许多正六边形(六条边相等,六个角也相等)构成,按图示的方法,利用三角尺和圆规画出一个正
六边形.
小结
角
定义
表示方法
有公共端点的两条射线组成的图形
一个数字或一个希腊字母表示
用一个大写字母表示
一条射线绕着它的端点旋转而成的图形
用三个大写字母表示
角
第四章 几何图形初步
角的定义
你能归纳出角的特点吗?用自己的话描述一下角是由什么组成的图形?
观察与思考
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
角的有关概念
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
始边
终边
O
A
B
(B)
平角
周角
想一想:如图,射线 OA 绕点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
说明:
在不做特别说明的情况下,我们说的角都指不大于平角的角
判断题:
(1)两条射线组成的图形叫角。
(2)角的大小与边的长短无关。
(3)角的 两边是两条射线。
A
B
C
.
.
.
1.角通常用三个大写字母及符号“∠”表示.三个大写字母应分别是顶点和两边上的任意点,顶点的字母必须写在中间.
角的表示
O
A
B
记作:
∠AOB
或
∠BOA
注意:顶点字母写在中间.
2.角也可用一个大写字母来表示,这个字母是表示顶点的大写字母,但当两个或两个以上的角有同一个顶点时,不能用一个大写字母表示.
O
∠O
记作:
条件:顶点处只有一个角.
3.角还可用一个数字或一个希腊字母表示,在角的内部靠近角的顶点处画一弧线,写上数字或希腊字母.
1
记作:∠1
有以新的方式出现的角吗
归纳:角也可以看成是由一条射线绕着它的端点旋转而形成的图形.
1. 图中有 个角,你能把它们表示出来吗?
3
练一练
A
E
C
O
∠AOE,∠COE,∠AOC.
2. 填写下表,将图中的角用不同方法表示出来.
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
角的度量
角的度量工具:
量角器
怎么知道这个角的大小?
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是 1 度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
A
O
B
如图,已知∠AOB,画∠EOF = ∠AOB,你有什么方法?
300
18000
38
9
0.6
0.01
38.25
5°= ′= ″;38.15°= ° ′;36″= ′= °;
38°15′= °.
练一练
例 如图,时钟显示为10:10时,时针与分针所夹
角度是 ( )
A.90° B.100° C.105° D.115°
解析:时针每小时旋转的夹角360°
÷12=30°,故10分钟,时针旋转的角度为5°,即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
练习
从蜂巢的入口处看,蜂巢由许多正六边形(六条边相等,六个角也相等)构成,按图示的方法,利用三角尺和圆规画出一个正
六边形.
小结
角
定义
表示方法
有公共端点的两条射线组成的图形
一个数字或一个希腊字母表示
用一个大写字母表示
一条射线绕着它的端点旋转而成的图形
用三个大写字母表示
