新课标高中数学常用公式及结论大全(理)
文档属性
| 名称 | 新课标高中数学常用公式及结论大全(理) |  | |
| 格式 | zip | ||
| 文件大小 | 687.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-03 19:23:49 | ||
图片预览




文档简介
PAGE
21
湖南省江华一中高考第二轮复习教学案-------新课标高中数学常用公式及结论大全(高考要必胜!基础是关键!)
必修1
1、集合的含义与表示
一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合。它具有三大特性:确定性、互异性、无序性。集合的表示有列举法、描述法。
描述法格式为:{元素|元素的特征},例如
2、常用数集及其表示方法
(1)自然数集N(又称非负整数集):0、1、2、3、……
(2)正整数集N*或N+ :1、2、3、……
(3)整数集Z:-2、-1、0、1、……
(4)有理数集Q:包含分数、整数、有限小数等
(5)实数集R:全体实数的集合
(6)空集Ф:不含任何元素的集合
3、元素与集合的关系:属于∈,不属于
例如:a是集合A的元素,就说a属于A,记作a∈A
4、集合与集合的关系:子集、真子集、相等
(1)子集的概念
如果集合A中的每一个元素都是集合B中的元素,那么集合A叫做集合B的子集(如图1),记作或.
若集合P中存在元素不是集合Q的元素,那么P不包含于Q,记作
(2)真子集的概念
若集合A是集合B的子集,且B中至少有一个元素不属于A,那么集合A叫做集合B的真子集(如图2). AB或BA.
(3)集合相等:若集合A中的元素与集合B中的元素完全相同则称集合A等于集合B,记作A=B.
5、重要结论
(1)传递性:若,,则
(2)空集Ф是任意集合的子集,是任意非空集合的真子集.
6、含有个元素的集合,它的子集个数共有 个;真子集有–1个;非空子集有–1个(即不计空集);非空的真子集有–2个.
7、集合的运算:交集、并集、补集
(1)一般地,由所有属于A又属于B的元素所组成的集合,叫做A,B的交集.记作A∩B(读作"A交B"),即A∩B={x|x∈A,且x∈B}.
(2)一般地,对于给定的两个集合A,B把它们所有的元素并在一起所组成的集合,叫做A,B的并集.记作A∪B(读作"A并B"),
即A∪B={x|x∈A,或x∈B}.
(3)若A是全集U的子集,由U中不属于A的元素构成的集合,叫做A在U中的补集,记作,
注:讨论集合的情况时,不要发遗忘了的情况。
8、映射与函数
(1)函数:如果A,B都是非空的数集,对于A中的任一元素x,在集合B中都有唯一确定的元素y与它对应f:A→B就叫做A到B的函数,记作y=f(x),其中x∈A,y∈B.集合A叫做函数y=f(x)的定义域,所有y组成的集合C(CB)叫做函数y=f(x)的值域.函数符号y=f(x)表示“y是x的函数”,有时简记作函数f(x).(2)映射:映射是函数的推广(A,B都是非空的集合)。
9、分段函数:在定义域的不同部分,有不同的对应法则的函数。如
10、求函数的定义域的原则:
(解决任何函数问题,必须要考虑其定义域)
①分式的分母不为零;
②偶次方根的被开方数大于或等于零;
③对数的底数大于0且不等于1;
④对数的真数大于0;
⑤指数为0的底不能为零;,则
11、函数的奇偶性(在整个定义域内考虑)
(1)奇函数满足,
奇函数的图象关于原点对称;
(2)偶函数满足,
偶函数的图象关于y轴对称;
注:①具有奇偶性的函数,其定义域关于原点对称; ②若奇函数在原点有定义,则
③根据奇偶性可将函数分为四类:奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数。
12、函数的单调性(在定义域的某个区间内考虑)
当时,都有,则在该区间上是增函数,图象从左到右上升;
当时,都有,则在该区间上是减函数,图象从左到右下降。
函数在某区间上是增函数或减函数,那么说在该区间具有单调性,该区间叫做单调(增/减)区间。
13、一元二次方程
(1)求根公式:
(2)判别式:
(3)时方程有两个不等实根;时方程有一个实根;时方程无实根。
(4)根与系数的关系——韦达定理:
,
14、二次函数:一般式;
顶点式
两根式
(1)顶点坐标为;
(2)对称轴方程为:x=;
(3)当时,图象是开口向上的抛物线,在x=处取得最小值
当时,图象是开口向下的抛物线,在x=处取得最大值
(4)二次函数图象与轴的交点个数和判别式的关系:
时,有两个交点;时,有一个交点(即顶点);时,无交点。
15、函数的零点
使的实数叫做函数的零点。例如是函数的一个零点。
注:函数有零点 函数的图象与轴有交点 方程有实根
16、函数零点的判定:
如果函数在区间上的图象是连续不断的一条曲线,并且有。那么,函数在区间内有零点,即存在。
17、分数指数幂 (,且)
(1).如;
(2) . 如;
(3);
(4)当为奇数时,;
当为偶数时,.
18、有理指数幂的运算性质()
(1); (2);
(3)
19、指数函数(且),其中
是自变量,叫做底数,定义域是R
图象
性质 (1)定义域:R
(2)值域:(0,+∞)
(3)过定点(0,1),即x=0时,y=1
(4)在 R上是增函数 (4)在R上是减函数
20、若,则 叫做以 为底的对数。
记作:(,) 其中,叫做对数的底数,叫做对数的真数。
注:指数式与对数式的互化公式:
21、对数的性质
(1)零和负数没有对数,即中;
(2)1的对数等于0,即 ;
底数的对数等于1,即
22、常用对数:以10为底的对数叫做常用对数,记为:
自然对数:以e(e=2.71828…)为底的对数叫做自然对数,记为:
23、对数恒等式:
24、对数的运算性质(a>0,a≠1,M>0,N>0)
(1);
(2) ;
(3) (注意公式的逆用)
25、对数的换底公式
(,且,,且, ).
推论①或; ②.
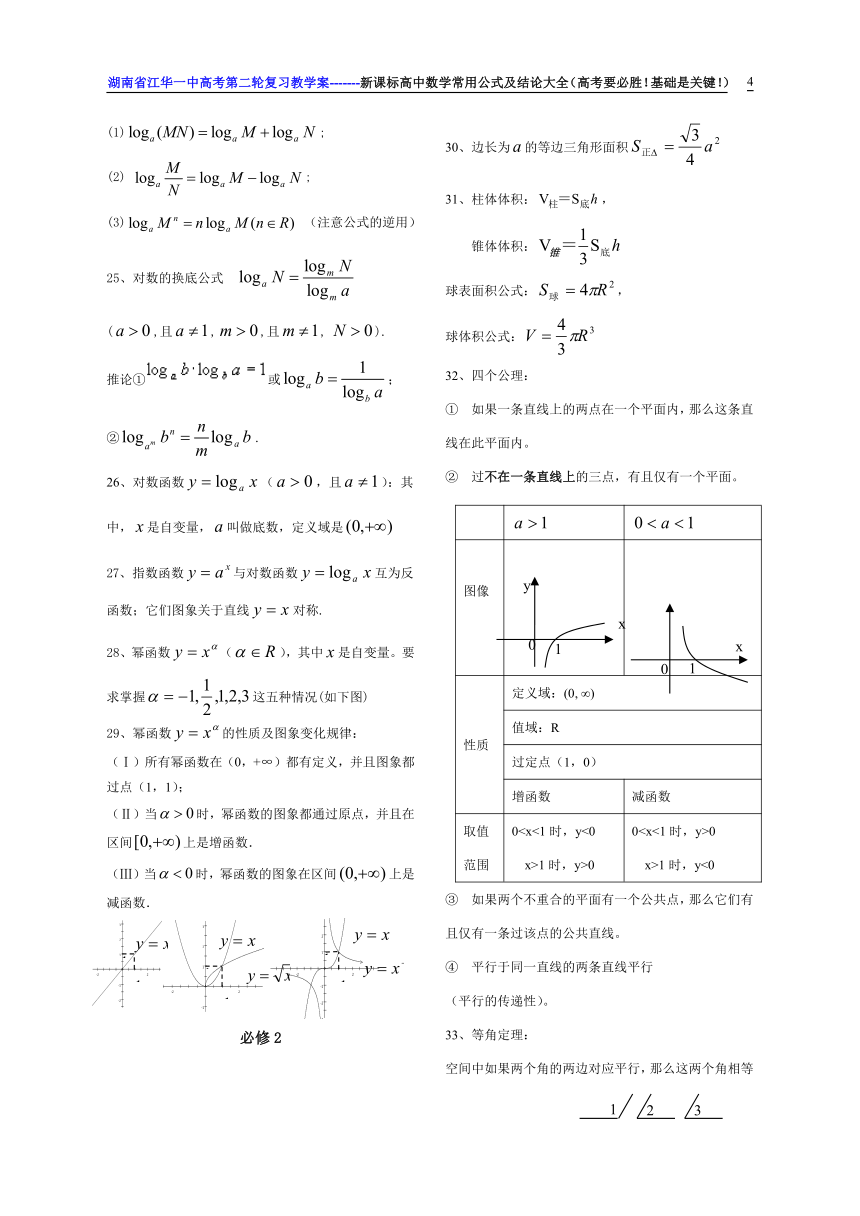
图像
性质 定义域:(0, ∞)
值域:R
过定点(1,0)
增函数 减函数
取值范围 01时,y>0 00 x>1时,y<0
26、对数函数(,且):其中,是自变量,叫做底数,定义域是
27、指数函数与对数函数互为反函数;它们图象关于直线对称.
28、幂函数(),其中是自变量。要求掌握这五种情况(如下图)
29、幂函数的性质及图象变化规律:
(Ⅰ)所有幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
(Ⅱ)当时,幂函数的图象都通过原点,并且在区间上是增函数.
(Ⅲ)当时,幂函数的图象在区间上是减函数.
必修2
30、边长为的等边三角形面积
31、柱体体积:,
锥体体积:
球表面积公式:,
球体积公式:
32、四个公理:
① 如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
② 过不在一条直线上的三点,有且仅有一个平面。
③ 如果两个不重合的平面有一个公共点,那么它们有且仅有一条过该点的公共直线。
④ 平行于同一直线的两条直线平行
(平行的传递性)。
33、等角定理:
空间中如果两个角的两边对应平行,那么这两个角相等或互补(如图)
34、两条直线的位置关系:
直线与平面的位置关系:
(1)直线在平面上;
(2)直线在平面外(包括直线与平面平行,直线与平面相交)
两个平面的位置关系:(1)两个平面平行;
(2)两个平面相交
35、直线与平面平行:
定义 一条直线与一个平面没有公共点,则这条直线与这个平面平行。
判定 平面外一条直线与此平面内的一直线平行,则该直线与此平面平行。
性质 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
36、平面与平面平行:
定义 两个平面没有公共点,则这两平面平行。
判定 若一个平面内有两条相交直线与另一个平面平行,则这两个平面平行。
性质 ① 如果两个平面平行,则其中一个面内的任一直线与另一个平面平行。
② 如果两个平行平面同时与第三个平面相交,那么它们交线平行。
37、直线与平面垂直:
定义 如果一条直线与一个平面内的任一直线都垂直,则这条直线与这个平面垂直。
判定 一条直线与一个平面内的两相交直线垂直,则这条直线与这个平面垂直。
性质 ①垂直于同一平面的两条直线平行。
②两平行直线中的一条与一个平面垂直,则另
一条也与这个平面垂直。
38、平面与平面垂直:
定义 两个平行相交,如果它们所成的二面角是直二面角,则这两个平面垂直。
判定 一个平面过另一个平面的垂线,则这两个平面垂直。
性质 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
39、三角形中“心”
(1)为的外心(各边垂直平分线的交点).外心到三个顶点的距离相等
(2)为的重心(各边中线的交点).重心将中线分成2:1的两段
(3)为的垂心(各边高的交点).
(4)为的内心(各内角平分线的交点). 内心到三边的距离相等
40、直线的斜率:
(1) 过两点的直线,斜率,()
(2)已知倾斜角为的直线,斜率(
(3)曲线在点(处的切线,其斜率
41、直线位置关系:已知两直线,则
特殊情况:(1)当都不存在时,;
(2)当不存在而时,
42、直线的五种方程 :
①点斜式
(直线过点,斜率为).
②斜截式
(直线在轴上的截距为,斜率为).
③两点式
(直线过两点与).
④截距式
(分别是直线在轴和轴上的截距,均不为0)
⑤一般式 (其中A、B不同时为0);可化为斜截式:
43、(1)平面上两点间的距离公式:|AB|=
(2)空间两点距离公式|AB|=
(3)点到直线的距离
(点,直线:).
44、两条平行直线与间的距离公式:
注:求直线的平行线,可设平行线为,求出即得。
45、求两相交直线与的交点:
解方程组
46、圆的方程:
①圆的标准方程 .
其中圆心为,半径为
②圆的一般方程 .
其中圆心为,半径为
,其中>0
47、直线与圆的位置关系
(1);
(2);
(3).
48、直线与圆相交于两点,求弦AB长度的公式:(1)
(2)
(结合韦达定理使用),其中是直线的斜率
49、两个圆的位置关系:设两圆的圆心分别为O1,O2,半径分别为r1,r2,
1);
2);
3); 4);
5)
必修③公式表
50、算法:是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
51、程序框图及结构
程序框 名称 功能
起止框 表示一个算法的起始和结束,是任何流程图不可少的。
输入、输出框 表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框 赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。
判断框 判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”。
52、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
53、三种抽样方法的区别与联系
类别 共同 各自特点 相互联系 适用范围
简单随机抽样 抽取过程中每个个体被抽取的概率相等 从总体中逐个抽取 总体中个体数较少
分层抽样 将总体分成几层进行抽取 各层抽样可采用简单随机抽样或系统抽样 总体有差异明显的几部分组成
系统抽样 将总体平均分成几部分,按事先确定的规则分别在各部分抽取 在起始部分抽样时采用简单随机抽样 总体中的个体较多
54、(1)频率分布直方图(注意其纵坐标是“频率/组距) , ,
。
(2)数字特征
众数:一组数据中,出现次数最多的数。
中位数:一组数从小到大排列,最中间的那个数
(若最中间有两个数,则取其平均数)。
平均数: 方差: =
标准差: 注:通过标准差或方差可以判断一组数据的分散程度;其值越小,数据越集中;其值越大,数据越分散。
回归直线方程:,其中,
55、事件的分类:
(1)必然事件:必然事件是每次试验都一定出现的事件。P(必然事件)=1
(2)不可能事件:任何一次试验都不可能出现的事件称为不可能事件。P(不可能事件)=0
(3)随机事件:随机试验的每一种结果或随机现象的每一种表现称作随机事件,简称为事件
基本事件:一个事件如果不能再被分解为两个或两个以上事件,称作基本事件。
56、在n次重复实验中,事件A发生的次数为m,则事件A发生的频率为m/n,当n很大时,m总是在某个常数值附近摆动,就把这个常数叫做事件A的概率。(概率范围:)
57、互斥事件概念:在一次随机事件中,不可能同时发生的两个事件,叫做互斥事件(如图1)。
如果事件A、B是互斥事件,
则P(A+B)=P(A)+P(B)
58、对立事件(如图2):指两个事件不可能同时发生,但必有一个发生。
0
sin 0 1
cos 1 0
0 1 不存在
sin 0 -1
cos - - - -1 0
- -1 - 0 不存在
对立事件性质:
P(A)+P()=1,其中表示事件A的对立事件。
59、古典概型是最简单的随机试验模型,古典概型有两个特征:
(1)基本事件个数是有限的;
(2)各基本事件的出现是等可能的,即它们发生的概率相同.
60、设一试验有n个等可能的基本事件,而事件A恰包含其中的m个基本事件,则事件A的概率P(A)公式为 =
运用互斥事件的概率加法公式时,首先要判断它们是否互斥,再由随机事件的概率公式分别求它们的概率,然后计算。 在计算某些事件的概率较复杂时,可转而先示对立事件的概率。
61、几何概型的概率公式:
必修④公式表
62、终边相同角构成的集合:
63、弧度计算公式:
64、扇形面积公式:
(为弧度)
65、三角函数的定义:
已知是的终边上除原点外的任一点
则
其中
66、三角函数值的符号
67、特殊角的三角函数值:
68、同角三角函数的关系:
69、和角与差角公式:
;
;
二倍角公式:
70、诱导公式 记忆口诀:奇变偶不变,符号看象限;其中,奇偶是指的个数,符号参考第66条.
71、辅助角公式:=(辅助角所在象限与点的象限相同,且 ).主要在求周期、单调性、最值时运用。 如
72、半角公式(降幂公式):
,
73、三角函数的性质()
(1)最小正周期;振幅为A;频率;相位:;初相:;值域:;
对称轴:由解得;
对称中心:由解得组成的点
(2)图象平移:左加右减、上加下减。
例如:向左平移1个单位,解析式变为
向下平移3个单位,解析式变为
(3)函数的最小正周期.
74、正弦定理:
在一个三角形中,各边与对应角正弦的比相等。
(R是三角形外接圆半径)
75、余弦定理:
推论
76、三角形的面积公式:
77、三角函数的图象与性质和性质
函数
图象
定义域
值域 [-1,1] [-1,1]
最大值 , ,
最小值 , ,
周期
奇偶性 奇函数 偶函数
单调性 在上是增函数 在上是增函数
在上是减函数 在上是减函数
三角函数
图象
定义域
值域
周期
奇偶性 奇函数
单调性 在上都是增函数
78、向量的三角形法则:
79、向量的平行四边形法则:
80、平面向量的坐标运算:
设向量a=,向量b=
(1)加法a+b=.
(2)减法a-b=.
(3)数乘a=
(4)数量积a·b=|a||b|cosθ=,
其中是这两个向量的夹角
(5)已知两点A,B,
则向量.
81、向量a=的模:|a|=,
即
82、两向量的夹角公式
83、向量的平行与垂直 (b0)
a||b b=λa .
记法: a=,b=
ab a·b=0 .
记法: a=,b=
必修⑤公式表
84、数列前项和与通项公式的关系:
( 数列的前n项和为).
85、等差、等比数列公式对比
等差数列 等比数列
定义式 ()
通项公式及推广式
中项公式 若成等差,则 若成等比,则
运算性质 ,则 若则
前项和公式
一个性质 成等差数列 成等比数列
86、解不等式
(1)、解一元二次不等式 :
①求判别式
②求一元二次方程的解 两相异实根 一个实根 没有实根
③画二次函数的图象
④结合图象写出解集
解集 R
解集
注:解集为R 对恒成立
(2)、含有绝对值的不等式 当a > 0时,有.[小于取中间]
或.
[大于取两边]
(3)分式不等式:先移项通分,化一边为0,再将除变乘,化为整式不等式,求解。
如解分式不等式 :先移项 通分
再除变乘,解出。
87、线性规划:
(1)一条直线将平面分为三部分(如图):
(2)不等式表示直线某一侧的平面区域,验证方法:取原点(0,0)代入不等式,若不等式成立,则平面区域在原点所在的一侧。假如直线恰好经过原点,则取其它点来验证,例如取点(1,0)。
(3)线性规划求最值问题:一般情况可以求出平面区域各个顶点的坐标,代入目标函数,最大的为最大值。
选修2-1
88、充要条件
(1)若则是的充分条件,是的必要条件.
(2)若,且,则是充要条件.
注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.
89、逻辑联结词。“p或q”记作:p∨q; “p且q”记作:p∧q; 非p记作:┐p
90、四种命题:
原命题:若p,则q 逆命题:若q,则p
否命题:若┐p,则┐q 逆否命题:若┐q,则┐p
注意:
(1)原命题与逆否命题同真同假,但逆命题的真假与否命题之间没有关系;
(2)┐p是指命题P的否定,注意区别“否命题”。例如命题P:“若,则”,那么P的“否命题”是:“若,则”,而┐p是:“若,则”。
91、全称命题:含有“任意”、“所有”等全称量词(记为)的命题,如P:
特称命题:含有“存在”、“有些”等存在量词(记为)的命题,如q:
注:全称命题的否定是特称命题,特称命题的否定是全称命题,
如上述命题p和q的否定:┐p:, ┐q:
92、椭圆
①定义:若F1,F2是两定点,P为动点,且(为常数)则P点的轨迹是椭圆。
②标准方程:焦点在x轴: ; 焦点在y轴: ;
长轴长=,短轴长=2b 焦距:2c 恒等式:a2-b2=c2 离心率:
93、双曲线
①定义:若F1,F2是两定点,(为常数),则动点P的轨迹是双曲线。
②图形:如图
③标准方程:
焦点在x轴:
焦点在y轴:
实轴长=,虚轴长=2b, 焦距:2c
恒等式:a2+b2=c2 离心率:
渐近线方程:当焦点在x轴时,渐近线方程为;当焦点在y轴时,渐近线方程为
等轴双曲线:当时,双曲线称为等轴双曲线,可设为。
94、抛物线
①定义:到定点F距离与到定直线的距离相等的点M的轨迹是抛物线(如左下图MF=MH)。
②图形:
方程 焦点: F F 准线方程:
图形:
方程:
焦点: F F
准线方程:
注意:几何特征:焦点到顶点的距离=;焦点到准线的距离=;
95. 空间向量与立体几何
(1).直线垂直,取直线的方向向量,则向量称为平面的法向量.
(2).若空间不重合两条直线,的方向向量分别为,,则,.
,
,,则
.
(3)若直线的方向向量为,平面的法向量为,且,则
,
.
(4).若空间不重合的两个平面,的法向量分别为,,则,
.
(5)设异面直线,的夹角为,方向向量为,,其夹角为,则有.
(6)设直线的方向向量为,平面的法向量为,与所成的角为,与的夹角为,则有.
(7)设,是二面角的两个面,的法向量,则向量,的夹角(或其补角)就是二面角的平面角的大小.若二面角的平面角为,则.
(8)、在直线上找一点,过定点且垂直于直线的向量为,则定点到直线的距离为.
(9)、点是平面外一点,是平面内的一定点,为平面的一个法向量,则点到平面的距离为.
选修2-2
96.导数的几何意义: 表示曲线在处的切线的斜率;
导数的物理意义: 表示运动物体在时刻处的瞬时速度。
97、几种常见函数的导数
(1) (C为常数).(2) .
(3) . (4) .
(5) ;
(6) ;;
(7)
导数的运算法则:
(1). (2).
(3).
复合函数求导法:
设函数y=f(u),u=(x),已知(x)在x处可导,f(u)在对应的点u(u=(x))处可导,则复合函数y=f[(x)]在点x处可导,且(f[(x)]=.
98.函数的单调性与其导函数的正负的关系:
在某个区间(a , b)内,如果,那么函数在这个区间内单调递增;
如果,那么函数在这个区间内单调递减。
注:若函数在这个区间内单调递增,则; 若函数在这个区间内单调递减,则
99、判别是极大(小)值的方法
(1)求导;
(2)令=0,
解方程,求出所有实根
(3)列表,判断每一个根左右两侧的正负情况: 如果在附近的左侧,右侧,则是极大值; 如果在附近的左侧,右侧,则是极小值.
100、求函数在闭区间[a , b]上的最值的步骤:
(1)求函数的所有极值;
(2)求闭区间端点函数值;
(3)将各极值与比较,其中最大的为最大值,最小的为最小值。
注意:(1)无论是极值还是最值,都是函数值,即,千万不能写成导数值。
(2)若在某区间内只有一个极值,则不用与端点比较也知道这个极值就是函数的最值。
101.定积分及应用
102、复数,
其中叫做实部,叫做虚部
(1)复数的相等 .()
(2)当a=0,b≠0时,z=bi为纯虚数;
(3)当b=0时,z=a为实数;
(4)复数z的共轭复数是
(5)复数的模=.
(6)i2 =-1, (-i)2 =-1.
(7) 复数对应复平面上的点,
103.复数的四则运算法则
(1)加:;
(2)减:;
(3)乘:;
类似多项式相乘
(4)除:(分子、分母乘分母共轭复数,此法称为“分母实数化”)
104、推理:
(1)合情推理:包含归纳推理(从特殊到一般)和类比推理(从特殊到特殊)
(2)演绎推理:从一般到特殊。三段论是演绎推理的一般模式,包括:大前提(已知的一般原理)、小前提(所研究的特殊情况)、结论(根据一般原理,对特殊情况得出的判断)
105、证明:
(1)直接证明:包括综合法(又叫由因导果法)和分析法(又叫执果索因法)
(2)间接证明:又叫反证法,通常假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立。
(3)用数学归纳法证明一个与正整数有关的命题的步骤:①证明:当取第一个值结论正确;②假设当(,≥)时结论正确,证明当时结论也正确由①②可知,命题对于从开始的所有正整数都正确.
数学归纳法被用来证明与自然数有关的命题:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
用数学归纳法证题时,两步缺一不可.
选修2-3
106.排列组合
(1)分类加法计数原理:做一件事情,完成它有N类办法,在第一类办法中有M1种不同的方法,在第二类办法中有M2种不同的方法,……,在第N类办法中有MN种不同的方法,那么完成这件事情共有M1+M2+……+MN种不同的方法。
(2)分步乘法计数原理:做一件事,完成它需要分成N个步骤,做第一 步有m1种不同的方法,做第二步有M2不同的方法,……,做第N步有MN不同的方法.那么完成这件事共有 N=M1M2...MN 种不同的方法。
(3)排列:从n个不同的元素中任取m(m≤n)个元素,按照一定顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列
(4)排列数:从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的一个排列. 从n个不同元素中取出m个元素的一个排列数,用符号表示。
当时为全排列.
(5)组合:从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合。组合数公式:
,
.
组合数性质:;.
(6).排列组合主要解题方法:
①优先法:特殊元素优先或特殊位置优先;
②捆绑法(相邻问题);
③插空法(不相邻问题);
④间接扣除法;(对有限制条件的问题,先从总体考虑,再把不符合条件的所有情况去掉)
⑤多排问题单排法;
⑥相同元素分组可采用隔板法(适用与指标分配,每部分至少有一个);
⑦先选后排,先分再排(注意等分分组问题);
⑧涂色问题(先分步考虑至某一步时再分类).
107.二项式定理:
⑴掌握二项展开式的通项:
;
⑵注意第r+1项二项式系数与第r+1项系数的区别.
(3)二项式系数具有下列性质:
①与首末两端等距离的二项式系数相等;
②若为偶数,中间一项(第项)的二项式系数最大;若为奇数,中间两项(第和项)的二项式系数最大.
③;
.
(4)二项式定理应用:用赋值法求展开式的某些项的系数的和如展开式的各项系数和为,奇数项系数和为 ,偶数项的系数和为.
108.概率与统计
(1)理解随机变量,离散型随机变量的定义,能够写出离散型随机变量的分布列。
(2)离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,..... ,xi ,......,xn
X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列
由概率的性质可知,任意离散型随机变量的分布列都具有下述两个性质:⑴; ⑵.
(2)二点分布:如果随机变量X的分布列为:
其中0(3)二项分布:记作为参数),
记.
… …
… …
(4)记住以下重要公式和结论:
⑴期望值.
⑵方差
.
⑶标准差;
.
⑷若(二项分布),则, .
⑸若(几何分布),则
,.
109.等可能事件的概率公式:
⑴; ⑵互斥事件有一个发生的概率公式为:;
⑶相互独立事件(事件A(或B)是否发生对事件B(或A)发生的概率没有影响)同时发生的概率公式为;
⑷独立重复试验概率公式;
⑸如果事件与互斥,那么事件与、与及事件与也都是互斥事件;
⑹如果事件、相互独立,那么事件、至少有一个不发生的概率是;
(7)如果事件与相互独立,那么事件与至少有 一个发生的概率是.
(8)条件概率:对任意事件A和事件B,在已知事件A发生的条件下事件B发生的概率,叫做条件概率.记作P(B|A),读作A发生的条件下B的概率
公式:
110.总体分布的估计:用样本估计总体,是研究统计问题的一个基本思想方法,一般地,样本容量越大,
这种估计就越精确,要求能画出频率分布表和频率分布直方图;
1 学会用样本平均数
估计总体平均数;
⑵会用样本方差
去估计总体方差及总体标准差;
(3).正态总体的概率密度函数:
,式中是参数,分别表示总体的平均数与标准差;
(4).正态曲线的性质:⑴曲线在时处于最高点,由这一点向左、向右两边延伸时,曲线逐渐降低;⑵曲线的对称轴位置由确定;曲线的形状由确定,越大,曲线越矮胖;反过来曲线越高瘦. ⑶曲线在轴上方,并且关于直线x= 对称;
(5).假设检验的基本思想(3原则):
正态总体在 以外取值的概率 只有4.6%,在 以外取值的概率只有0.3% 由于这些概率很小,通常称这些情况发生为小概率事件.也就是说,通常认为这些情况在一次试验中几乎是不可能发生的.
⑴提出统计假设,确定随机变量服从正态分布;
⑵确定一次试验中的取值是否落入范围;
⑶作出推断:如果,接受统计假设;如果,由于这是小概率事件,就拒绝假设.
111. 独立性检验
假设有两个分类变量X和Y,它们的值域分另为{x1, x2}和{y1, y2},其样本频数列联表为:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
若要推断的论述为H1:“X与Y有关系”,可以利用独立性检验来考察两个变量是否有关系,并且能较精确地给出这种判断的可靠程度。具体的做法是,由表中的数据算出随机变量K^2的值(即K的平方) K2 = n (ad - bc) 2 / [(a+b)(c+d)(a+c)(b+d)],其中n=a+b+c+d为样本容量,K2的值越大,说明“X与Y有关系”成立的可能性越大。
K2≤3.841时,X与Y无关; K2>3.841时,X与Y有95%可能性有关;K2>6.635时X与Y有99%可能性有关
回归分析: 回归直线方程 , 其中
,
选修4-1几何证明选讲
112.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边
推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰
113.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例
推论:平行于三角形的一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
114.判定两个三角形相似的方法:
预备定理:平行于三角形一边的直线和其他两边(或延长线)相交,所构成的三角形相似
判定定理1:两角对应相等,两三角形相似
判定定理2:两边对应成比例且夹角相等两三角形相似
判定定理3:三边对应成比例,两三角形相似
引理:若一条直线截三角形两边(或延长线)所得的对应线段成比例,那么直线平行第三边
相似三角形的性质定理:
1)相似三角形对应高、中线、角平分线的比都等于相似比; 2)相似三角形周长的比等于相似比
3)相似三角形面积的比等于相似比的平方
115.直角三角形的射影定理
如图△ABC中,CD是斜边AB上的高,则
(1)
(2)
(3);
116.圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半
圆心角定理:圆心角的度数等于它所对弧的度数
推论1:同弧或等弧所对的圆周角相等
推论2:半圆(或直径)所对的圆周角为直角
117.圆的切线的性质定理:圆的切线垂直于经过切点的半径
推论1:经过圆心垂直于切线的直线必经过切点
推论2:经过切点垂直于切线的直线必经过圆心
圆的切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线
118.弦切角定理:弦切角等于它所夹的弧所对的圆周角, 如图:
119.与圆有关的定理:
(1)相交弦定理:圆内两条相交弦,
被交点分成的两条线段长的积相等;
(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等;
(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项;
(4)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
选修4-4坐标系与参数方程
120、极坐标系:其中
(1)如图,
点M的极坐标为
(2)极坐标与直角坐标的互化公式:
①;
②,
121、参数方程形如………(*)
参数方程是借助参数,间接给出之间的关系,而普通方程是直接给出与的关系,如
(1)圆的参数方程是
(2)椭圆的参数方程
(3)参数方程与普通方程的互化:消去参数方程的参数,得到普通方程。
消去参数的方法有:
①公式法:用公式等
②代入法:方程(*)中,由解出,代入
③加减消元法:方程(*)中,两式相加(减)消去参数;请将圆的参数方程,化为圆的标准方程__________________,说说你用的是什么方法?
提示:解参数方程问题,通常先将参数方程化为普通方程,再求解。
选修4—5不等式选讲
122、几个重要不等式
①(当且仅当时取).
②(基本不等式) ,(当且仅当时取到等号).
变形公式:
用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.
③(三个正数的算术—几何平均不等式)(当且仅当时取到等号).
④绝对值三角不等式
⑤二维形式的柯西不等式: 当且仅当时,等号成立.
三维形式的柯西不等式:
123.含有两个(或两个以上)绝对值的不等式的解法:
规律:找零点、划区间、分段讨论去绝对值、每段中取交集,最后取各段的并集.
124、恒成立问题
⑴不等式的解集是全体实数(或恒成立)的条件是:①当时
②当时
⑵不等式的解集是全体实数(或恒成立)的条件是:①当时
②当时
⑶恒成立
恒成立
⑷恒成立
恒成立
选修4-7 优选法
0
B
+
)
—
—
+
+
准线
F
x
1
0
y
1
1
x
F
A
A,B
(图1)
或
AB
(图2)
AB
A
B
A
2
3
—
—
+
—
+
—
+
直线
·
极点O
极径
点M
)极角
极轴
y
x
x
y
0
x
0
1
y
1
0
y
x
1
1
1
1
1
1
:(不同在任何一个平面内的两条直线,
没有公共点)
:(在同一平面内,没有公共点)
:(在同一平面内,有一个公共点)
其中是圆心到直线的距离,且
x
)
P(x,y)
y
r
-
0
y
x
x
0
1
-1
-
y
a+b
a
-1
1
0
x
y
b
b-a
b
a
M
H
2
^
1(
D
B
A
C
图(2)
A B
图1
A
B
C
B
A
a+b
b
a
直线
极小值
极大值
PAGE
21
湖南省江华一中高考第二轮复习教学案-------新课标高中数学常用公式及结论大全(高考要必胜!基础是关键!)
必修1
1、集合的含义与表示
一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合。它具有三大特性:确定性、互异性、无序性。集合的表示有列举法、描述法。
描述法格式为:{元素|元素的特征},例如
2、常用数集及其表示方法
(1)自然数集N(又称非负整数集):0、1、2、3、……
(2)正整数集N*或N+ :1、2、3、……
(3)整数集Z:-2、-1、0、1、……
(4)有理数集Q:包含分数、整数、有限小数等
(5)实数集R:全体实数的集合
(6)空集Ф:不含任何元素的集合
3、元素与集合的关系:属于∈,不属于
例如:a是集合A的元素,就说a属于A,记作a∈A
4、集合与集合的关系:子集、真子集、相等
(1)子集的概念
如果集合A中的每一个元素都是集合B中的元素,那么集合A叫做集合B的子集(如图1),记作或.
若集合P中存在元素不是集合Q的元素,那么P不包含于Q,记作
(2)真子集的概念
若集合A是集合B的子集,且B中至少有一个元素不属于A,那么集合A叫做集合B的真子集(如图2). AB或BA.
(3)集合相等:若集合A中的元素与集合B中的元素完全相同则称集合A等于集合B,记作A=B.
5、重要结论
(1)传递性:若,,则
(2)空集Ф是任意集合的子集,是任意非空集合的真子集.
6、含有个元素的集合,它的子集个数共有 个;真子集有–1个;非空子集有–1个(即不计空集);非空的真子集有–2个.
7、集合的运算:交集、并集、补集
(1)一般地,由所有属于A又属于B的元素所组成的集合,叫做A,B的交集.记作A∩B(读作"A交B"),即A∩B={x|x∈A,且x∈B}.
(2)一般地,对于给定的两个集合A,B把它们所有的元素并在一起所组成的集合,叫做A,B的并集.记作A∪B(读作"A并B"),
即A∪B={x|x∈A,或x∈B}.
(3)若A是全集U的子集,由U中不属于A的元素构成的集合,叫做A在U中的补集,记作,
注:讨论集合的情况时,不要发遗忘了的情况。
8、映射与函数
(1)函数:如果A,B都是非空的数集,对于A中的任一元素x,在集合B中都有唯一确定的元素y与它对应f:A→B就叫做A到B的函数,记作y=f(x),其中x∈A,y∈B.集合A叫做函数y=f(x)的定义域,所有y组成的集合C(CB)叫做函数y=f(x)的值域.函数符号y=f(x)表示“y是x的函数”,有时简记作函数f(x).(2)映射:映射是函数的推广(A,B都是非空的集合)。
9、分段函数:在定义域的不同部分,有不同的对应法则的函数。如
10、求函数的定义域的原则:
(解决任何函数问题,必须要考虑其定义域)
①分式的分母不为零;
②偶次方根的被开方数大于或等于零;
③对数的底数大于0且不等于1;
④对数的真数大于0;
⑤指数为0的底不能为零;,则
11、函数的奇偶性(在整个定义域内考虑)
(1)奇函数满足,
奇函数的图象关于原点对称;
(2)偶函数满足,
偶函数的图象关于y轴对称;
注:①具有奇偶性的函数,其定义域关于原点对称; ②若奇函数在原点有定义,则
③根据奇偶性可将函数分为四类:奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数。
12、函数的单调性(在定义域的某个区间内考虑)
当时,都有,则在该区间上是增函数,图象从左到右上升;
当时,都有,则在该区间上是减函数,图象从左到右下降。
函数在某区间上是增函数或减函数,那么说在该区间具有单调性,该区间叫做单调(增/减)区间。
13、一元二次方程
(1)求根公式:
(2)判别式:
(3)时方程有两个不等实根;时方程有一个实根;时方程无实根。
(4)根与系数的关系——韦达定理:
,
14、二次函数:一般式;
顶点式
两根式
(1)顶点坐标为;
(2)对称轴方程为:x=;
(3)当时,图象是开口向上的抛物线,在x=处取得最小值
当时,图象是开口向下的抛物线,在x=处取得最大值
(4)二次函数图象与轴的交点个数和判别式的关系:
时,有两个交点;时,有一个交点(即顶点);时,无交点。
15、函数的零点
使的实数叫做函数的零点。例如是函数的一个零点。
注:函数有零点 函数的图象与轴有交点 方程有实根
16、函数零点的判定:
如果函数在区间上的图象是连续不断的一条曲线,并且有。那么,函数在区间内有零点,即存在。
17、分数指数幂 (,且)
(1).如;
(2) . 如;
(3);
(4)当为奇数时,;
当为偶数时,.
18、有理指数幂的运算性质()
(1); (2);
(3)
19、指数函数(且),其中
是自变量,叫做底数,定义域是R
图象
性质 (1)定义域:R
(2)值域:(0,+∞)
(3)过定点(0,1),即x=0时,y=1
(4)在 R上是增函数 (4)在R上是减函数
20、若,则 叫做以 为底的对数。
记作:(,) 其中,叫做对数的底数,叫做对数的真数。
注:指数式与对数式的互化公式:
21、对数的性质
(1)零和负数没有对数,即中;
(2)1的对数等于0,即 ;
底数的对数等于1,即
22、常用对数:以10为底的对数叫做常用对数,记为:
自然对数:以e(e=2.71828…)为底的对数叫做自然对数,记为:
23、对数恒等式:
24、对数的运算性质(a>0,a≠1,M>0,N>0)
(1);
(2) ;
(3) (注意公式的逆用)
25、对数的换底公式
(,且,,且, ).
推论①或; ②.
图像
性质 定义域:(0, ∞)
值域:R
过定点(1,0)
增函数 减函数
取值范围 0
26、对数函数(,且):其中,是自变量,叫做底数,定义域是
27、指数函数与对数函数互为反函数;它们图象关于直线对称.
28、幂函数(),其中是自变量。要求掌握这五种情况(如下图)
29、幂函数的性质及图象变化规律:
(Ⅰ)所有幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
(Ⅱ)当时,幂函数的图象都通过原点,并且在区间上是增函数.
(Ⅲ)当时,幂函数的图象在区间上是减函数.
必修2
30、边长为的等边三角形面积
31、柱体体积:,
锥体体积:
球表面积公式:,
球体积公式:
32、四个公理:
① 如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
② 过不在一条直线上的三点,有且仅有一个平面。
③ 如果两个不重合的平面有一个公共点,那么它们有且仅有一条过该点的公共直线。
④ 平行于同一直线的两条直线平行
(平行的传递性)。
33、等角定理:
空间中如果两个角的两边对应平行,那么这两个角相等或互补(如图)
34、两条直线的位置关系:
直线与平面的位置关系:
(1)直线在平面上;
(2)直线在平面外(包括直线与平面平行,直线与平面相交)
两个平面的位置关系:(1)两个平面平行;
(2)两个平面相交
35、直线与平面平行:
定义 一条直线与一个平面没有公共点,则这条直线与这个平面平行。
判定 平面外一条直线与此平面内的一直线平行,则该直线与此平面平行。
性质 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
36、平面与平面平行:
定义 两个平面没有公共点,则这两平面平行。
判定 若一个平面内有两条相交直线与另一个平面平行,则这两个平面平行。
性质 ① 如果两个平面平行,则其中一个面内的任一直线与另一个平面平行。
② 如果两个平行平面同时与第三个平面相交,那么它们交线平行。
37、直线与平面垂直:
定义 如果一条直线与一个平面内的任一直线都垂直,则这条直线与这个平面垂直。
判定 一条直线与一个平面内的两相交直线垂直,则这条直线与这个平面垂直。
性质 ①垂直于同一平面的两条直线平行。
②两平行直线中的一条与一个平面垂直,则另
一条也与这个平面垂直。
38、平面与平面垂直:
定义 两个平行相交,如果它们所成的二面角是直二面角,则这两个平面垂直。
判定 一个平面过另一个平面的垂线,则这两个平面垂直。
性质 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
39、三角形中“心”
(1)为的外心(各边垂直平分线的交点).外心到三个顶点的距离相等
(2)为的重心(各边中线的交点).重心将中线分成2:1的两段
(3)为的垂心(各边高的交点).
(4)为的内心(各内角平分线的交点). 内心到三边的距离相等
40、直线的斜率:
(1) 过两点的直线,斜率,()
(2)已知倾斜角为的直线,斜率(
(3)曲线在点(处的切线,其斜率
41、直线位置关系:已知两直线,则
特殊情况:(1)当都不存在时,;
(2)当不存在而时,
42、直线的五种方程 :
①点斜式
(直线过点,斜率为).
②斜截式
(直线在轴上的截距为,斜率为).
③两点式
(直线过两点与).
④截距式
(分别是直线在轴和轴上的截距,均不为0)
⑤一般式 (其中A、B不同时为0);可化为斜截式:
43、(1)平面上两点间的距离公式:|AB|=
(2)空间两点距离公式|AB|=
(3)点到直线的距离
(点,直线:).
44、两条平行直线与间的距离公式:
注:求直线的平行线,可设平行线为,求出即得。
45、求两相交直线与的交点:
解方程组
46、圆的方程:
①圆的标准方程 .
其中圆心为,半径为
②圆的一般方程 .
其中圆心为,半径为
,其中>0
47、直线与圆的位置关系
(1);
(2);
(3).
48、直线与圆相交于两点,求弦AB长度的公式:(1)
(2)
(结合韦达定理使用),其中是直线的斜率
49、两个圆的位置关系:设两圆的圆心分别为O1,O2,半径分别为r1,r2,
1);
2);
3); 4);
5)
必修③公式表
50、算法:是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
51、程序框图及结构
程序框 名称 功能
起止框 表示一个算法的起始和结束,是任何流程图不可少的。
输入、输出框 表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置。
处理框 赋值、计算,算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。
判断框 判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时标明“否”或“N”。
52、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
53、三种抽样方法的区别与联系
类别 共同 各自特点 相互联系 适用范围
简单随机抽样 抽取过程中每个个体被抽取的概率相等 从总体中逐个抽取 总体中个体数较少
分层抽样 将总体分成几层进行抽取 各层抽样可采用简单随机抽样或系统抽样 总体有差异明显的几部分组成
系统抽样 将总体平均分成几部分,按事先确定的规则分别在各部分抽取 在起始部分抽样时采用简单随机抽样 总体中的个体较多
54、(1)频率分布直方图(注意其纵坐标是“频率/组距) , ,
。
(2)数字特征
众数:一组数据中,出现次数最多的数。
中位数:一组数从小到大排列,最中间的那个数
(若最中间有两个数,则取其平均数)。
平均数: 方差: =
标准差: 注:通过标准差或方差可以判断一组数据的分散程度;其值越小,数据越集中;其值越大,数据越分散。
回归直线方程:,其中,
55、事件的分类:
(1)必然事件:必然事件是每次试验都一定出现的事件。P(必然事件)=1
(2)不可能事件:任何一次试验都不可能出现的事件称为不可能事件。P(不可能事件)=0
(3)随机事件:随机试验的每一种结果或随机现象的每一种表现称作随机事件,简称为事件
基本事件:一个事件如果不能再被分解为两个或两个以上事件,称作基本事件。
56、在n次重复实验中,事件A发生的次数为m,则事件A发生的频率为m/n,当n很大时,m总是在某个常数值附近摆动,就把这个常数叫做事件A的概率。(概率范围:)
57、互斥事件概念:在一次随机事件中,不可能同时发生的两个事件,叫做互斥事件(如图1)。
如果事件A、B是互斥事件,
则P(A+B)=P(A)+P(B)
58、对立事件(如图2):指两个事件不可能同时发生,但必有一个发生。
0
sin 0 1
cos 1 0
0 1 不存在
sin 0 -1
cos - - - -1 0
- -1 - 0 不存在
对立事件性质:
P(A)+P()=1,其中表示事件A的对立事件。
59、古典概型是最简单的随机试验模型,古典概型有两个特征:
(1)基本事件个数是有限的;
(2)各基本事件的出现是等可能的,即它们发生的概率相同.
60、设一试验有n个等可能的基本事件,而事件A恰包含其中的m个基本事件,则事件A的概率P(A)公式为 =
运用互斥事件的概率加法公式时,首先要判断它们是否互斥,再由随机事件的概率公式分别求它们的概率,然后计算。 在计算某些事件的概率较复杂时,可转而先示对立事件的概率。
61、几何概型的概率公式:
必修④公式表
62、终边相同角构成的集合:
63、弧度计算公式:
64、扇形面积公式:
(为弧度)
65、三角函数的定义:
已知是的终边上除原点外的任一点
则
其中
66、三角函数值的符号
67、特殊角的三角函数值:
68、同角三角函数的关系:
69、和角与差角公式:
;
;
二倍角公式:
70、诱导公式 记忆口诀:奇变偶不变,符号看象限;其中,奇偶是指的个数,符号参考第66条.
71、辅助角公式:=(辅助角所在象限与点的象限相同,且 ).主要在求周期、单调性、最值时运用。 如
72、半角公式(降幂公式):
,
73、三角函数的性质()
(1)最小正周期;振幅为A;频率;相位:;初相:;值域:;
对称轴:由解得;
对称中心:由解得组成的点
(2)图象平移:左加右减、上加下减。
例如:向左平移1个单位,解析式变为
向下平移3个单位,解析式变为
(3)函数的最小正周期.
74、正弦定理:
在一个三角形中,各边与对应角正弦的比相等。
(R是三角形外接圆半径)
75、余弦定理:
推论
76、三角形的面积公式:
77、三角函数的图象与性质和性质
函数
图象
定义域
值域 [-1,1] [-1,1]
最大值 , ,
最小值 , ,
周期
奇偶性 奇函数 偶函数
单调性 在上是增函数 在上是增函数
在上是减函数 在上是减函数
三角函数
图象
定义域
值域
周期
奇偶性 奇函数
单调性 在上都是增函数
78、向量的三角形法则:
79、向量的平行四边形法则:
80、平面向量的坐标运算:
设向量a=,向量b=
(1)加法a+b=.
(2)减法a-b=.
(3)数乘a=
(4)数量积a·b=|a||b|cosθ=,
其中是这两个向量的夹角
(5)已知两点A,B,
则向量.
81、向量a=的模:|a|=,
即
82、两向量的夹角公式
83、向量的平行与垂直 (b0)
a||b b=λa .
记法: a=,b=
ab a·b=0 .
记法: a=,b=
必修⑤公式表
84、数列前项和与通项公式的关系:
( 数列的前n项和为).
85、等差、等比数列公式对比
等差数列 等比数列
定义式 ()
通项公式及推广式
中项公式 若成等差,则 若成等比,则
运算性质 ,则 若则
前项和公式
一个性质 成等差数列 成等比数列
86、解不等式
(1)、解一元二次不等式 :
①求判别式
②求一元二次方程的解 两相异实根 一个实根 没有实根
③画二次函数的图象
④结合图象写出解集
解集 R
解集
注:解集为R 对恒成立
(2)、含有绝对值的不等式 当a > 0时,有.[小于取中间]
或.
[大于取两边]
(3)分式不等式:先移项通分,化一边为0,再将除变乘,化为整式不等式,求解。
如解分式不等式 :先移项 通分
再除变乘,解出。
87、线性规划:
(1)一条直线将平面分为三部分(如图):
(2)不等式表示直线某一侧的平面区域,验证方法:取原点(0,0)代入不等式,若不等式成立,则平面区域在原点所在的一侧。假如直线恰好经过原点,则取其它点来验证,例如取点(1,0)。
(3)线性规划求最值问题:一般情况可以求出平面区域各个顶点的坐标,代入目标函数,最大的为最大值。
选修2-1
88、充要条件
(1)若则是的充分条件,是的必要条件.
(2)若,且,则是充要条件.
注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.
89、逻辑联结词。“p或q”记作:p∨q; “p且q”记作:p∧q; 非p记作:┐p
90、四种命题:
原命题:若p,则q 逆命题:若q,则p
否命题:若┐p,则┐q 逆否命题:若┐q,则┐p
注意:
(1)原命题与逆否命题同真同假,但逆命题的真假与否命题之间没有关系;
(2)┐p是指命题P的否定,注意区别“否命题”。例如命题P:“若,则”,那么P的“否命题”是:“若,则”,而┐p是:“若,则”。
91、全称命题:含有“任意”、“所有”等全称量词(记为)的命题,如P:
特称命题:含有“存在”、“有些”等存在量词(记为)的命题,如q:
注:全称命题的否定是特称命题,特称命题的否定是全称命题,
如上述命题p和q的否定:┐p:, ┐q:
92、椭圆
①定义:若F1,F2是两定点,P为动点,且(为常数)则P点的轨迹是椭圆。
②标准方程:焦点在x轴: ; 焦点在y轴: ;
长轴长=,短轴长=2b 焦距:2c 恒等式:a2-b2=c2 离心率:
93、双曲线
①定义:若F1,F2是两定点,(为常数),则动点P的轨迹是双曲线。
②图形:如图
③标准方程:
焦点在x轴:
焦点在y轴:
实轴长=,虚轴长=2b, 焦距:2c
恒等式:a2+b2=c2 离心率:
渐近线方程:当焦点在x轴时,渐近线方程为;当焦点在y轴时,渐近线方程为
等轴双曲线:当时,双曲线称为等轴双曲线,可设为。
94、抛物线
①定义:到定点F距离与到定直线的距离相等的点M的轨迹是抛物线(如左下图MF=MH)。
②图形:
方程 焦点: F F 准线方程:
图形:
方程:
焦点: F F
准线方程:
注意:几何特征:焦点到顶点的距离=;焦点到准线的距离=;
95. 空间向量与立体几何
(1).直线垂直,取直线的方向向量,则向量称为平面的法向量.
(2).若空间不重合两条直线,的方向向量分别为,,则,.
,
,,则
.
(3)若直线的方向向量为,平面的法向量为,且,则
,
.
(4).若空间不重合的两个平面,的法向量分别为,,则,
.
(5)设异面直线,的夹角为,方向向量为,,其夹角为,则有.
(6)设直线的方向向量为,平面的法向量为,与所成的角为,与的夹角为,则有.
(7)设,是二面角的两个面,的法向量,则向量,的夹角(或其补角)就是二面角的平面角的大小.若二面角的平面角为,则.
(8)、在直线上找一点,过定点且垂直于直线的向量为,则定点到直线的距离为.
(9)、点是平面外一点,是平面内的一定点,为平面的一个法向量,则点到平面的距离为.
选修2-2
96.导数的几何意义: 表示曲线在处的切线的斜率;
导数的物理意义: 表示运动物体在时刻处的瞬时速度。
97、几种常见函数的导数
(1) (C为常数).(2) .
(3) . (4) .
(5) ;
(6) ;;
(7)
导数的运算法则:
(1). (2).
(3).
复合函数求导法:
设函数y=f(u),u=(x),已知(x)在x处可导,f(u)在对应的点u(u=(x))处可导,则复合函数y=f[(x)]在点x处可导,且(f[(x)]=.
98.函数的单调性与其导函数的正负的关系:
在某个区间(a , b)内,如果,那么函数在这个区间内单调递增;
如果,那么函数在这个区间内单调递减。
注:若函数在这个区间内单调递增,则; 若函数在这个区间内单调递减,则
99、判别是极大(小)值的方法
(1)求导;
(2)令=0,
解方程,求出所有实根
(3)列表,判断每一个根左右两侧的正负情况: 如果在附近的左侧,右侧,则是极大值; 如果在附近的左侧,右侧,则是极小值.
100、求函数在闭区间[a , b]上的最值的步骤:
(1)求函数的所有极值;
(2)求闭区间端点函数值;
(3)将各极值与比较,其中最大的为最大值,最小的为最小值。
注意:(1)无论是极值还是最值,都是函数值,即,千万不能写成导数值。
(2)若在某区间内只有一个极值,则不用与端点比较也知道这个极值就是函数的最值。
101.定积分及应用
102、复数,
其中叫做实部,叫做虚部
(1)复数的相等 .()
(2)当a=0,b≠0时,z=bi为纯虚数;
(3)当b=0时,z=a为实数;
(4)复数z的共轭复数是
(5)复数的模=.
(6)i2 =-1, (-i)2 =-1.
(7) 复数对应复平面上的点,
103.复数的四则运算法则
(1)加:;
(2)减:;
(3)乘:;
类似多项式相乘
(4)除:(分子、分母乘分母共轭复数,此法称为“分母实数化”)
104、推理:
(1)合情推理:包含归纳推理(从特殊到一般)和类比推理(从特殊到特殊)
(2)演绎推理:从一般到特殊。三段论是演绎推理的一般模式,包括:大前提(已知的一般原理)、小前提(所研究的特殊情况)、结论(根据一般原理,对特殊情况得出的判断)
105、证明:
(1)直接证明:包括综合法(又叫由因导果法)和分析法(又叫执果索因法)
(2)间接证明:又叫反证法,通常假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立。
(3)用数学归纳法证明一个与正整数有关的命题的步骤:①证明:当取第一个值结论正确;②假设当(,≥)时结论正确,证明当时结论也正确由①②可知,命题对于从开始的所有正整数都正确.
数学归纳法被用来证明与自然数有关的命题:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
用数学归纳法证题时,两步缺一不可.
选修2-3
106.排列组合
(1)分类加法计数原理:做一件事情,完成它有N类办法,在第一类办法中有M1种不同的方法,在第二类办法中有M2种不同的方法,……,在第N类办法中有MN种不同的方法,那么完成这件事情共有M1+M2+……+MN种不同的方法。
(2)分步乘法计数原理:做一件事,完成它需要分成N个步骤,做第一 步有m1种不同的方法,做第二步有M2不同的方法,……,做第N步有MN不同的方法.那么完成这件事共有 N=M1M2...MN 种不同的方法。
(3)排列:从n个不同的元素中任取m(m≤n)个元素,按照一定顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列
(4)排列数:从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的一个排列. 从n个不同元素中取出m个元素的一个排列数,用符号表示。
当时为全排列.
(5)组合:从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合。组合数公式:
,
.
组合数性质:;.
(6).排列组合主要解题方法:
①优先法:特殊元素优先或特殊位置优先;
②捆绑法(相邻问题);
③插空法(不相邻问题);
④间接扣除法;(对有限制条件的问题,先从总体考虑,再把不符合条件的所有情况去掉)
⑤多排问题单排法;
⑥相同元素分组可采用隔板法(适用与指标分配,每部分至少有一个);
⑦先选后排,先分再排(注意等分分组问题);
⑧涂色问题(先分步考虑至某一步时再分类).
107.二项式定理:
⑴掌握二项展开式的通项:
;
⑵注意第r+1项二项式系数与第r+1项系数的区别.
(3)二项式系数具有下列性质:
①与首末两端等距离的二项式系数相等;
②若为偶数,中间一项(第项)的二项式系数最大;若为奇数,中间两项(第和项)的二项式系数最大.
③;
.
(4)二项式定理应用:用赋值法求展开式的某些项的系数的和如展开式的各项系数和为,奇数项系数和为 ,偶数项的系数和为.
108.概率与统计
(1)理解随机变量,离散型随机变量的定义,能够写出离散型随机变量的分布列。
(2)离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,..... ,xi ,......,xn
X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列
由概率的性质可知,任意离散型随机变量的分布列都具有下述两个性质:⑴; ⑵.
(2)二点分布:如果随机变量X的分布列为:
其中0
记.
… …
… …
(4)记住以下重要公式和结论:
⑴期望值.
⑵方差
.
⑶标准差;
.
⑷若(二项分布),则, .
⑸若(几何分布),则
,.
109.等可能事件的概率公式:
⑴; ⑵互斥事件有一个发生的概率公式为:;
⑶相互独立事件(事件A(或B)是否发生对事件B(或A)发生的概率没有影响)同时发生的概率公式为;
⑷独立重复试验概率公式;
⑸如果事件与互斥,那么事件与、与及事件与也都是互斥事件;
⑹如果事件、相互独立,那么事件、至少有一个不发生的概率是;
(7)如果事件与相互独立,那么事件与至少有 一个发生的概率是.
(8)条件概率:对任意事件A和事件B,在已知事件A发生的条件下事件B发生的概率,叫做条件概率.记作P(B|A),读作A发生的条件下B的概率
公式:
110.总体分布的估计:用样本估计总体,是研究统计问题的一个基本思想方法,一般地,样本容量越大,
这种估计就越精确,要求能画出频率分布表和频率分布直方图;
1 学会用样本平均数
估计总体平均数;
⑵会用样本方差
去估计总体方差及总体标准差;
(3).正态总体的概率密度函数:
,式中是参数,分别表示总体的平均数与标准差;
(4).正态曲线的性质:⑴曲线在时处于最高点,由这一点向左、向右两边延伸时,曲线逐渐降低;⑵曲线的对称轴位置由确定;曲线的形状由确定,越大,曲线越矮胖;反过来曲线越高瘦. ⑶曲线在轴上方,并且关于直线x= 对称;
(5).假设检验的基本思想(3原则):
正态总体在 以外取值的概率 只有4.6%,在 以外取值的概率只有0.3% 由于这些概率很小,通常称这些情况发生为小概率事件.也就是说,通常认为这些情况在一次试验中几乎是不可能发生的.
⑴提出统计假设,确定随机变量服从正态分布;
⑵确定一次试验中的取值是否落入范围;
⑶作出推断:如果,接受统计假设;如果,由于这是小概率事件,就拒绝假设.
111. 独立性检验
假设有两个分类变量X和Y,它们的值域分另为{x1, x2}和{y1, y2},其样本频数列联表为:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
若要推断的论述为H1:“X与Y有关系”,可以利用独立性检验来考察两个变量是否有关系,并且能较精确地给出这种判断的可靠程度。具体的做法是,由表中的数据算出随机变量K^2的值(即K的平方) K2 = n (ad - bc) 2 / [(a+b)(c+d)(a+c)(b+d)],其中n=a+b+c+d为样本容量,K2的值越大,说明“X与Y有关系”成立的可能性越大。
K2≤3.841时,X与Y无关; K2>3.841时,X与Y有95%可能性有关;K2>6.635时X与Y有99%可能性有关
回归分析: 回归直线方程 , 其中
,
选修4-1几何证明选讲
112.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推论1:经过三角形一边的中点与另一边平行的直线必平分第三边
推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰
113.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例
推论:平行于三角形的一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
114.判定两个三角形相似的方法:
预备定理:平行于三角形一边的直线和其他两边(或延长线)相交,所构成的三角形相似
判定定理1:两角对应相等,两三角形相似
判定定理2:两边对应成比例且夹角相等两三角形相似
判定定理3:三边对应成比例,两三角形相似
引理:若一条直线截三角形两边(或延长线)所得的对应线段成比例,那么直线平行第三边
相似三角形的性质定理:
1)相似三角形对应高、中线、角平分线的比都等于相似比; 2)相似三角形周长的比等于相似比
3)相似三角形面积的比等于相似比的平方
115.直角三角形的射影定理
如图△ABC中,CD是斜边AB上的高,则
(1)
(2)
(3);
116.圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半
圆心角定理:圆心角的度数等于它所对弧的度数
推论1:同弧或等弧所对的圆周角相等
推论2:半圆(或直径)所对的圆周角为直角
117.圆的切线的性质定理:圆的切线垂直于经过切点的半径
推论1:经过圆心垂直于切线的直线必经过切点
推论2:经过切点垂直于切线的直线必经过圆心
圆的切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线
118.弦切角定理:弦切角等于它所夹的弧所对的圆周角, 如图:
119.与圆有关的定理:
(1)相交弦定理:圆内两条相交弦,
被交点分成的两条线段长的积相等;
(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等;
(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项;
(4)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
选修4-4坐标系与参数方程
120、极坐标系:其中
(1)如图,
点M的极坐标为
(2)极坐标与直角坐标的互化公式:
①;
②,
121、参数方程形如………(*)
参数方程是借助参数,间接给出之间的关系,而普通方程是直接给出与的关系,如
(1)圆的参数方程是
(2)椭圆的参数方程
(3)参数方程与普通方程的互化:消去参数方程的参数,得到普通方程。
消去参数的方法有:
①公式法:用公式等
②代入法:方程(*)中,由解出,代入
③加减消元法:方程(*)中,两式相加(减)消去参数;请将圆的参数方程,化为圆的标准方程__________________,说说你用的是什么方法?
提示:解参数方程问题,通常先将参数方程化为普通方程,再求解。
选修4—5不等式选讲
122、几个重要不等式
①(当且仅当时取).
②(基本不等式) ,(当且仅当时取到等号).
变形公式:
用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.
③(三个正数的算术—几何平均不等式)(当且仅当时取到等号).
④绝对值三角不等式
⑤二维形式的柯西不等式: 当且仅当时,等号成立.
三维形式的柯西不等式:
123.含有两个(或两个以上)绝对值的不等式的解法:
规律:找零点、划区间、分段讨论去绝对值、每段中取交集,最后取各段的并集.
124、恒成立问题
⑴不等式的解集是全体实数(或恒成立)的条件是:①当时
②当时
⑵不等式的解集是全体实数(或恒成立)的条件是:①当时
②当时
⑶恒成立
恒成立
⑷恒成立
恒成立
选修4-7 优选法
0
B
+
)
—
—
+
+
准线
F
x
1
0
y
1
1
x
F
A
A,B
(图1)
或
AB
(图2)
AB
A
B
A
2
3
—
—
+
—
+
—
+
直线
·
极点O
极径
点M
)极角
极轴
y
x
x
y
0
x
0
1
y
1
0
y
x
1
1
1
1
1
1
:(不同在任何一个平面内的两条直线,
没有公共点)
:(在同一平面内,没有公共点)
:(在同一平面内,有一个公共点)
其中是圆心到直线的距离,且
x
)
P(x,y)
y
r
-
0
y
x
x
0
1
-1
-
y
a+b
a
-1
1
0
x
y
b
b-a
b
a
M
H
2
^
1(
D
B
A
C
图(2)
A B
图1
A
B
C
B
A
a+b
b
a
直线
极小值
极大值
PAGE
同课章节目录
