4.1.1 n次方根与分数指数幂 课件(共32张PPT)
文档属性
| 名称 | 4.1.1 n次方根与分数指数幂 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 05:59:38 | ||
图片预览










文档简介
(共32张PPT)
第四章 指数函数与对数函数
4.1.1 n次方根与分数指数幂
学习目标
1.理解n次方根及根式的概念,掌握根式的性质.(重点)
2.能利用根式的性质对根式进行运算.(重点、难点、易错点)
3.理解分数指数幂的含义,掌握根式与分数指数幂的互化.(重点、难点)
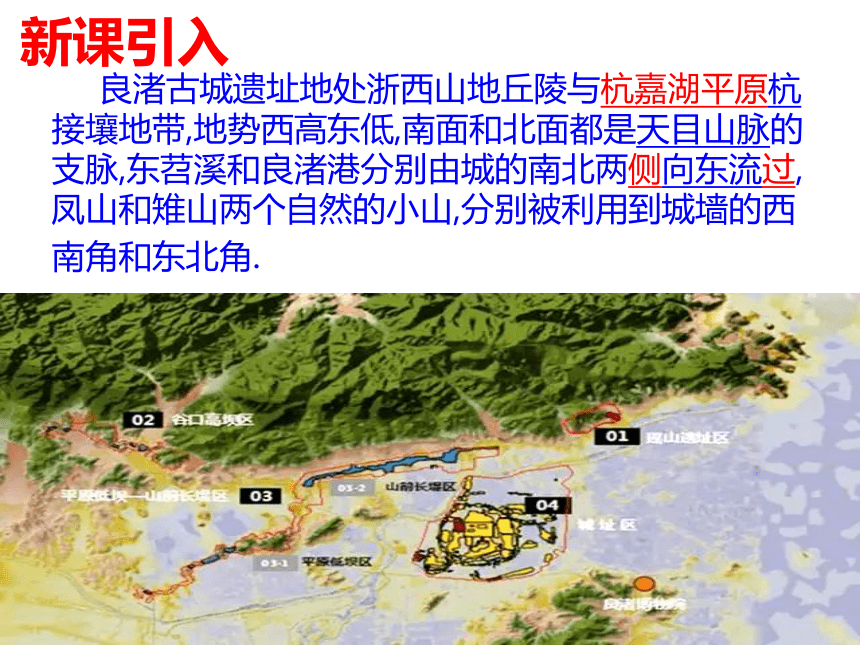
良渚古城遗址地处浙西山地丘陵与杭嘉湖平原杭接壤地带,地势西高东低,南面和北面都是天目山脉的支脉,东苕溪和良渚港分别由城的南北两侧向东流过,凤山和雉山两个自然的小山,分别被利用到城墙的西南角和东北角.
新课引入
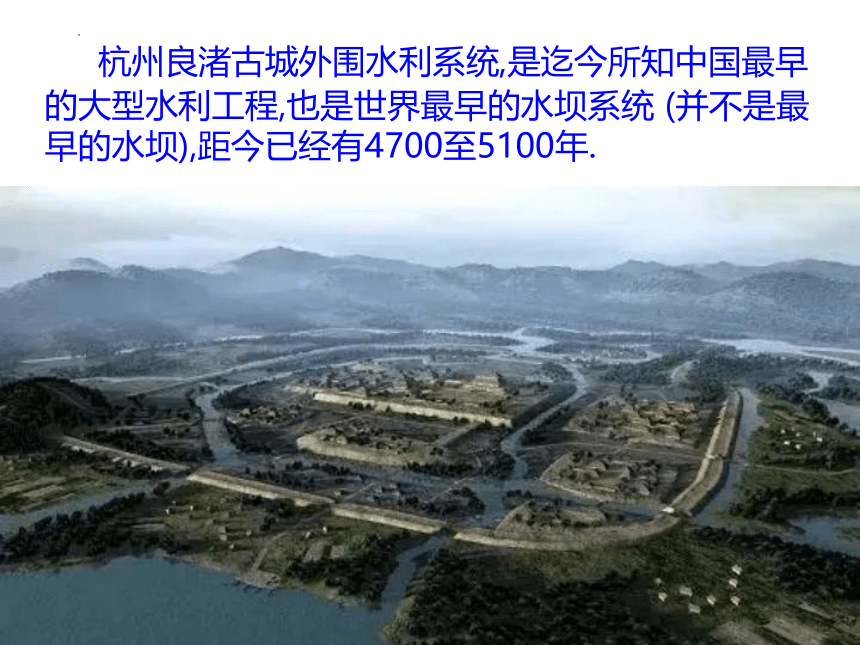
杭州良渚古城外围水利系统,是迄今所知中国最早的大型水利工程,也是世界最早的水坝系统 (并不是最早的水坝),距今已经有4700至5100年.
2019年7月6日下午,在阿塞拜疆首都巴库举行的联合国教科文组织第43届世界遗产委员会会议上,随着大会主席阿布法斯·加拉耶夫落槌,位于浙江杭州的“良渚古城遗址”成功列入《世界遗产名录》,中华文明五千多年历史得到实证,遗产地的价值以及真实性、完整性得到了世界范围的认可.
你知道考古学家在测定遗址年代时用了什么数学知识吗
在学习幂函数时,我们把正方形场地边长c关于面积S的函数 ,像 这样分数为指数的幂,其意义是什么呢?下面从已知的平方根、
立方根的意义入手展开研究.
为了研究指数函数,我们需要把指数的范围拓展
到全体实数.初中我们已经学过整数指数幂.
温故知新
思考1:4的平方根是多少?任何一个实数都有平方根吗?一个数的平方根有几个?
思考2:-27的立方根是多少?任何一个实数都有立方根吗?一个数的立方根有几个?
±2;
非负数才有平方根;
2个
-3;
任何实数都有立方根;
1个
温故知新
思考3:一般地,实常数a的平方根、立方根是什么概念?
平方根:如果x2=a,那么x叫做a的平方根.
立方根:如果x3=a,那么x叫做a的立方根.
平方根:如果x2=a,那么x叫做a的平方根.
立方根:如果x3=a,那么x叫做a的立方根.
思考5:如果 , , ,
类比上面的说法,你有什么结论?
思考6:推广到一般情形,a的n次方根
是一个什么概念?试给出其定义。
探究新知
探究新知
n次方根:一般地,如果xn=a,那么x叫做a的n次方根,其中,n>1,且n∈N*
a
a的平方根
4
9
0
-4
-9
a
a的立方根
27
8
0
-8
-27
a
a的五次方根
32
1
0
-1
-32
±2
±3
0
3
2
0
-2
-3
2
1
0
-1
-2
a
a的四次方根
81
16
0
-16
-81
±3
±2
0
探究新知
a=
x
n
a
a的立方根
27
8
0
-8
-27
3
2
0
-2
-3
a
a的五次方根
32
1
0
-1
-32
2
1
0
-1
-2
n为奇数时:
a只有一个n次方根
a是正数时,a的奇数次方根是正数
a是负数时,a的奇数次方根是负数
探究新知
n为偶数时:
a是正数时,有两个互为相反数
的偶数次方根
负的偶数次方根记为:
正的偶数次方根记为:
a
a的平方根
4
9
0
-4
-9
±2
±3
0
a
a的四次方根
81
16
0
-16
-81
±3
±2
0
a是负数时,没有偶数次方根
探究新知
a
a的平方根
4
9
0
-4
-9
a
a的立方根
27
8
0
-8
-27
a
a的五次方根
32
1
0
-1
-32
±2
±3
0
3
2
0
-2
-3
2
1
0
-1
-2
a
a的四次方根
81
16
0
-16
-81
±3
±2
0
0的任何次方根都是0,即=0
(当n是奇数)
(当n是偶数,且a>0)
(1)
(2)0的任何次方根是
(3)负数没有偶次方根.
0
归纳总结:
根指数
根式
被开方数
式子 叫做根式,这里 n 叫做根指数, a 叫做被开方数
学习新知
结论: .
1.根据方根的意义确定下面式子的值:
练一练
(1)= ;
(2)= ;
(3)= .
a
探究新知
结论:
学习新知
探究 根据n次方根的定义和运算,我们知道
___________________(a>0)
___________________(a>0)
也就是说,当根式的被开方数(看成幂的形式)的指数能被根指数整除时,根式可以表示成分数指数幂的形式.
思考 当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
事实上,任何一个根式都可以表示为分数指数幂的形式
例如:
, .
一般地
规定正数的正分数指数幂的意义是:
所以,在条件的下,根式都可以写成分数指数幂的形式. 正数的负分数指数幂的意义与负整数指数幂的意义相仿.
规定正数的负分数指数幂的意义是:
例如,
规定0的正分数指数幂等于0,0的负分数指数幂没意义.
把下列的分数指数式化为根式,把根式化成分数指数式.
练一练
(1)= ; (2)= ;
(3)= ; (4)= .
答案:(1) ; (2) ;
(3) ; (4) .
练习:课本第107页练习1
整数指数幂的运算性质对于有理指数幂也同样适用,有如下运算性质:
例2 求值:(1) ;(2) .
解:
(1)法一;
(2)法一.
法二;
法二.
法三.
练一练
(1)= ; (2)
(3) (4)
求值:
答案:(1)8 ; (2) ;
(3) ; (4) 2 .
解:
例3 用分数指数幂的形式表示并计算下列各式( 其中a>0).
; .
(1) ;
(2) .
例4 计算下式各式(式中字母均是正数).
教材P107页练习1,2,3
解:
解:
解:
请同学们谈谈本节课的收获与体会.
本节课你学到了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题?
课堂小结
第四章 指数函数与对数函数
4.1.1 n次方根与分数指数幂
学习目标
1.理解n次方根及根式的概念,掌握根式的性质.(重点)
2.能利用根式的性质对根式进行运算.(重点、难点、易错点)
3.理解分数指数幂的含义,掌握根式与分数指数幂的互化.(重点、难点)
良渚古城遗址地处浙西山地丘陵与杭嘉湖平原杭接壤地带,地势西高东低,南面和北面都是天目山脉的支脉,东苕溪和良渚港分别由城的南北两侧向东流过,凤山和雉山两个自然的小山,分别被利用到城墙的西南角和东北角.
新课引入
杭州良渚古城外围水利系统,是迄今所知中国最早的大型水利工程,也是世界最早的水坝系统 (并不是最早的水坝),距今已经有4700至5100年.
2019年7月6日下午,在阿塞拜疆首都巴库举行的联合国教科文组织第43届世界遗产委员会会议上,随着大会主席阿布法斯·加拉耶夫落槌,位于浙江杭州的“良渚古城遗址”成功列入《世界遗产名录》,中华文明五千多年历史得到实证,遗产地的价值以及真实性、完整性得到了世界范围的认可.
你知道考古学家在测定遗址年代时用了什么数学知识吗
在学习幂函数时,我们把正方形场地边长c关于面积S的函数 ,像 这样分数为指数的幂,其意义是什么呢?下面从已知的平方根、
立方根的意义入手展开研究.
为了研究指数函数,我们需要把指数的范围拓展
到全体实数.初中我们已经学过整数指数幂.
温故知新
思考1:4的平方根是多少?任何一个实数都有平方根吗?一个数的平方根有几个?
思考2:-27的立方根是多少?任何一个实数都有立方根吗?一个数的立方根有几个?
±2;
非负数才有平方根;
2个
-3;
任何实数都有立方根;
1个
温故知新
思考3:一般地,实常数a的平方根、立方根是什么概念?
平方根:如果x2=a,那么x叫做a的平方根.
立方根:如果x3=a,那么x叫做a的立方根.
平方根:如果x2=a,那么x叫做a的平方根.
立方根:如果x3=a,那么x叫做a的立方根.
思考5:如果 , , ,
类比上面的说法,你有什么结论?
思考6:推广到一般情形,a的n次方根
是一个什么概念?试给出其定义。
探究新知
探究新知
n次方根:一般地,如果xn=a,那么x叫做a的n次方根,其中,n>1,且n∈N*
a
a的平方根
4
9
0
-4
-9
a
a的立方根
27
8
0
-8
-27
a
a的五次方根
32
1
0
-1
-32
±2
±3
0
3
2
0
-2
-3
2
1
0
-1
-2
a
a的四次方根
81
16
0
-16
-81
±3
±2
0
探究新知
a=
x
n
a
a的立方根
27
8
0
-8
-27
3
2
0
-2
-3
a
a的五次方根
32
1
0
-1
-32
2
1
0
-1
-2
n为奇数时:
a只有一个n次方根
a是正数时,a的奇数次方根是正数
a是负数时,a的奇数次方根是负数
探究新知
n为偶数时:
a是正数时,有两个互为相反数
的偶数次方根
负的偶数次方根记为:
正的偶数次方根记为:
a
a的平方根
4
9
0
-4
-9
±2
±3
0
a
a的四次方根
81
16
0
-16
-81
±3
±2
0
a是负数时,没有偶数次方根
探究新知
a
a的平方根
4
9
0
-4
-9
a
a的立方根
27
8
0
-8
-27
a
a的五次方根
32
1
0
-1
-32
±2
±3
0
3
2
0
-2
-3
2
1
0
-1
-2
a
a的四次方根
81
16
0
-16
-81
±3
±2
0
0的任何次方根都是0,即=0
(当n是奇数)
(当n是偶数,且a>0)
(1)
(2)0的任何次方根是
(3)负数没有偶次方根.
0
归纳总结:
根指数
根式
被开方数
式子 叫做根式,这里 n 叫做根指数, a 叫做被开方数
学习新知
结论: .
1.根据方根的意义确定下面式子的值:
练一练
(1)= ;
(2)= ;
(3)= .
a
探究新知
结论:
学习新知
探究 根据n次方根的定义和运算,我们知道
___________________(a>0)
___________________(a>0)
也就是说,当根式的被开方数(看成幂的形式)的指数能被根指数整除时,根式可以表示成分数指数幂的形式.
思考 当根式的被开方数的指数不能被根指数整除时,根式是否也能表示为分数指数幂的形式呢?
事实上,任何一个根式都可以表示为分数指数幂的形式
例如:
, .
一般地
规定正数的正分数指数幂的意义是:
所以,在条件的下,根式都可以写成分数指数幂的形式. 正数的负分数指数幂的意义与负整数指数幂的意义相仿.
规定正数的负分数指数幂的意义是:
例如,
规定0的正分数指数幂等于0,0的负分数指数幂没意义.
把下列的分数指数式化为根式,把根式化成分数指数式.
练一练
(1)= ; (2)= ;
(3)= ; (4)= .
答案:(1) ; (2) ;
(3) ; (4) .
练习:课本第107页练习1
整数指数幂的运算性质对于有理指数幂也同样适用,有如下运算性质:
例2 求值:(1) ;(2) .
解:
(1)法一;
(2)法一.
法二;
法二.
法三.
练一练
(1)= ; (2)
(3) (4)
求值:
答案:(1)8 ; (2) ;
(3) ; (4) 2 .
解:
例3 用分数指数幂的形式表示并计算下列各式( 其中a>0).
; .
(1) ;
(2) .
例4 计算下式各式(式中字母均是正数).
教材P107页练习1,2,3
解:
解:
解:
请同学们谈谈本节课的收获与体会.
本节课你学到了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题?
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
