人教A版(2019)选择性必修第一册 3.1.1椭圆及其标准方程 课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 3.1.1椭圆及其标准方程 课件(共24张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
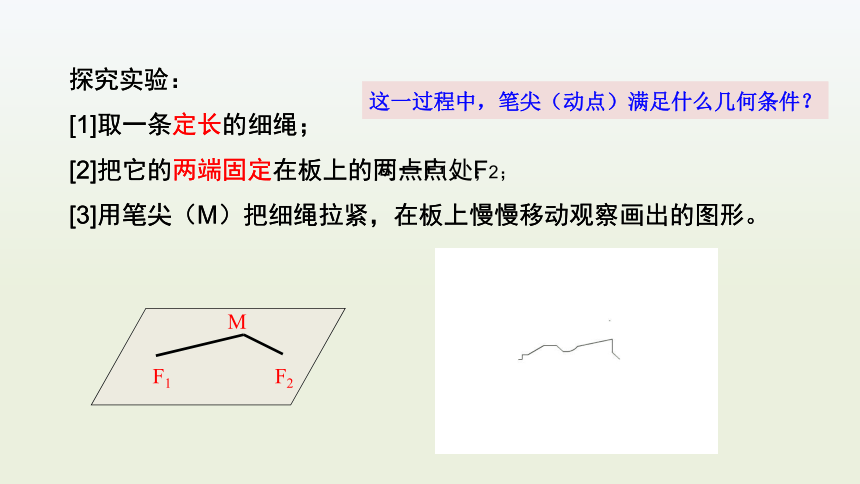
吊坠
镜子
对称的车标
美丽的建筑外观
生活中的椭圆
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
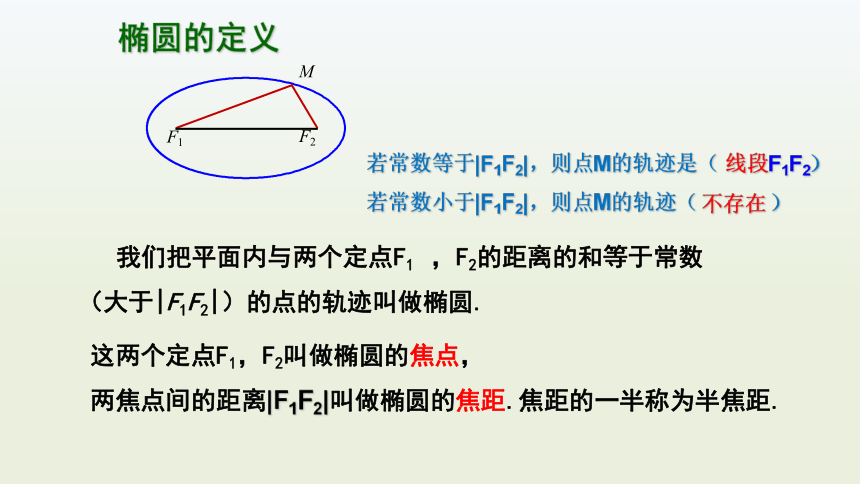
探究实验:
[1]取一条定长的细绳;
[2]把它的两端固定在板上的同一点处;
[3]用笔尖(M)把细绳拉紧,在板上慢慢移动观察画出的图形。
探究实验:
[1]取一条定长的细绳;
[2]把它的两端固定在板上的两点F1、F2;
[3]用笔尖(M)把细绳拉紧,在板上慢慢移动观察画出的图形。
F1
F2
M
这一过程中,笔尖(动点)满足什么几何条件?
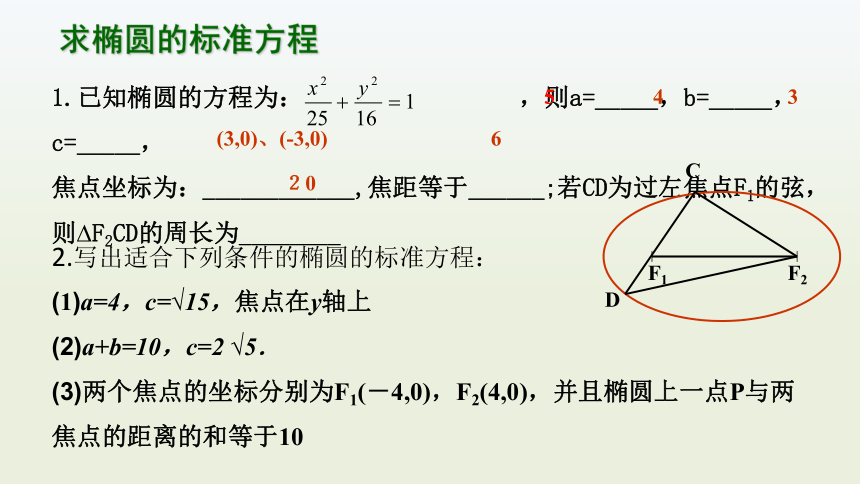
我们把平面内与两个定点F1 ,F2的距离的和等于常数
(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点F1,F2叫做椭圆的焦点,
两焦点间的距离|F1F2|叫做椭圆的焦距.焦距的一半称为半焦距.
椭圆的定义
F1
F2
M
若常数等于|F1F2|,则点M的轨迹是( )
若常数小于|F1F2|,则点M的轨迹( )
线段F1F2
不存在
椭圆的方程的推导
如图,已知焦点为F1,F2的椭圆,M是椭圆上任一点,试推导椭圆的方程.
解:以经过椭圆焦点 F1,F2 的直线为 x 轴,线段F1F2的中垂线为y轴,建立直角坐标系xoy.
设 M(x,y)是椭圆上任一点,
设椭圆的焦距为 2c,点M与两焦点的距离之和为常数 2a.
我们把它叫做的椭圆的标准方程.它的焦点在 轴上.
则方程可化为
令
焦点在y轴:
焦点在x轴:
y
o
F1
F2
M
x
两类标准方程
o
F2
y
x
F1
M
(x,y)
(x,y)
a, b, c三者中a最大,
哪个变量对应的分母大,焦点就在哪个轴上
1.已知椭圆的方程为: ,则a=_____,b=_____,c=_____,
焦点坐标为:____________,焦距等于______;若CD为过左焦点F1的弦,
则 F2CD的周长为________
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
2.写出适合下列条件的椭圆的标准方程:
(1)a=4,c=√15,焦点在y轴上
(2)a+b=10,c=2 √5.
(3)两个焦点的坐标分别为F1(-4,0),F2(4,0),并且椭圆上一点P与两焦点的距离的和等于10
求椭圆的标准方程
解法一:因为椭圆的焦点在x轴上,所以设它
的标准方程为:
①
②
联立①②,
因此, 所求椭圆的标准方程为:
又∵焦点的坐标为
3.已知椭圆的两个焦点坐标分别是(-2,0), (2,0), 并且经过点 .求它的标准方程.
3.已知椭圆的两个焦点坐标分别是(-2,0), (2,0), 并且经过点 .求它的标准方程.
解法二:因为椭圆的焦点在x轴上,所以设
它的标准方程为
由椭圆的定义知
因此, 所求椭圆的标准方程为
所以
又因为 ,所以
5.(1)若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆,求k的取值范围.
∵方程表示的曲线是焦点在y轴上的椭圆
解之得:0∴k的取值范围为0平面内与两个定点F1,F2的距离的和等于常数(大于| F1F2 |)的点的轨迹叫做椭圆.
标准方程
不 同 点
相 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
x
y
F1
F2
M
O
x
y
F1
F2
M
O
△椭圆中的焦点三角形问题
y
o
F1
F2
x
△与椭圆有关的轨迹问题
△与椭圆有关的轨迹问题
△与椭圆有关的轨迹问题
吊坠
镜子
对称的车标
美丽的建筑外观
生活中的椭圆
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
探究实验:
[1]取一条定长的细绳;
[2]把它的两端固定在板上的同一点处;
[3]用笔尖(M)把细绳拉紧,在板上慢慢移动观察画出的图形。
探究实验:
[1]取一条定长的细绳;
[2]把它的两端固定在板上的两点F1、F2;
[3]用笔尖(M)把细绳拉紧,在板上慢慢移动观察画出的图形。
F1
F2
M
这一过程中,笔尖(动点)满足什么几何条件?
我们把平面内与两个定点F1 ,F2的距离的和等于常数
(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点F1,F2叫做椭圆的焦点,
两焦点间的距离|F1F2|叫做椭圆的焦距.焦距的一半称为半焦距.
椭圆的定义
F1
F2
M
若常数等于|F1F2|,则点M的轨迹是( )
若常数小于|F1F2|,则点M的轨迹( )
线段F1F2
不存在
椭圆的方程的推导
如图,已知焦点为F1,F2的椭圆,M是椭圆上任一点,试推导椭圆的方程.
解:以经过椭圆焦点 F1,F2 的直线为 x 轴,线段F1F2的中垂线为y轴,建立直角坐标系xoy.
设 M(x,y)是椭圆上任一点,
设椭圆的焦距为 2c,点M与两焦点的距离之和为常数 2a.
我们把它叫做的椭圆的标准方程.它的焦点在 轴上.
则方程可化为
令
焦点在y轴:
焦点在x轴:
y
o
F1
F2
M
x
两类标准方程
o
F2
y
x
F1
M
(x,y)
(x,y)
a, b, c三者中a最大,
哪个变量对应的分母大,焦点就在哪个轴上
1.已知椭圆的方程为: ,则a=_____,b=_____,c=_____,
焦点坐标为:____________,焦距等于______;若CD为过左焦点F1的弦,
则 F2CD的周长为________
5
4
3
(3,0)、(-3,0)
6
20
F1
F2
C
D
2.写出适合下列条件的椭圆的标准方程:
(1)a=4,c=√15,焦点在y轴上
(2)a+b=10,c=2 √5.
(3)两个焦点的坐标分别为F1(-4,0),F2(4,0),并且椭圆上一点P与两焦点的距离的和等于10
求椭圆的标准方程
解法一:因为椭圆的焦点在x轴上,所以设它
的标准方程为:
①
②
联立①②,
因此, 所求椭圆的标准方程为:
又∵焦点的坐标为
3.已知椭圆的两个焦点坐标分别是(-2,0), (2,0), 并且经过点 .求它的标准方程.
3.已知椭圆的两个焦点坐标分别是(-2,0), (2,0), 并且经过点 .求它的标准方程.
解法二:因为椭圆的焦点在x轴上,所以设
它的标准方程为
由椭圆的定义知
因此, 所求椭圆的标准方程为
所以
又因为 ,所以
5.(1)若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆,求k的取值范围.
∵方程表示的曲线是焦点在y轴上的椭圆
解之得:0
标准方程
不 同 点
相 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
x
y
F1
F2
M
O
x
y
F1
F2
M
O
△椭圆中的焦点三角形问题
y
o
F1
F2
x
△与椭圆有关的轨迹问题
△与椭圆有关的轨迹问题
△与椭圆有关的轨迹问题
