两数和的平方(浙江省宁波市奉化市)
文档属性
| 名称 | 两数和的平方(浙江省宁波市奉化市) |  | |
| 格式 | rar | ||
| 文件大小 | 664.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-25 21:23:00 | ||
图片预览





文档简介
课件12张PPT。14.3.2 两数和平方楼旭美慈溪市金山中学多项式乘以多项式:( m+n)(a+b) =ma+mb+na+nb平方差公式 : (a+b)(a-b)=a2-b2一.知识回顾
1(x+y)(x+y) =
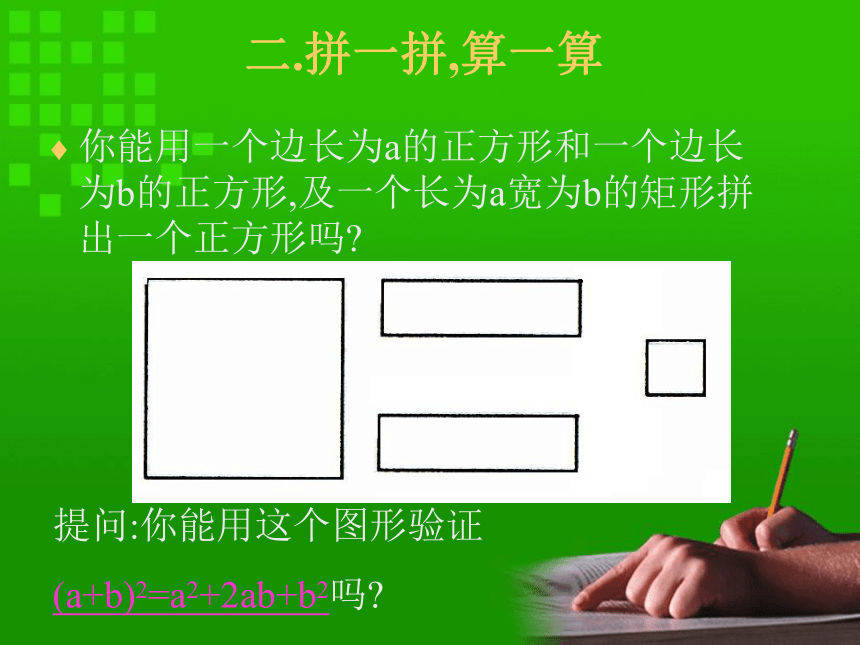
x2+2xy+y2a2+4ab+4b20.25m2+2mn+n2做一做,并观察等式的左边和右边你发现有什么规律。2 (a+2b)(a+2b) =3 ( 0.5m+n)(0.5m+n) =2(2ab)(2b)2(0.5)22(0.5mn)二.拼一拼,算一算你能用一个边长为a的正方形和一个边长为b的正方形,及一个长为a宽为b的矩形拼出一个正方形吗?提问:你能用这个图形验证
(a+b)2=a2+2ab+b2吗?三.想一想你会用(a + b)2=a2+2ab+b2计算(a-b)2吗?解:(a-b)2=[a+(-b)]2两数差的平方:(a-b)2=a2-2ab+b2 =a2+2a(-b)+b2
=a2-2ab+b2四.实践与探索右图是用4个长为a、宽为b的矩形拼
成的正方形,中间留下的“洞”恰好是
一个小正方形,用不同的方法计算中
间小正方形的面积,你发现了什么?解:因为s小正方形=s大正方形 -4s矩形 故s小正方形=(a+b)2-4ab =a2+2ab+b2-4ab =a2-2ab+b2又有图可知小正方形的边长为(a-b),所以
S小正方形=(a-b)2所以(a-b)2=a2-2ab+b2ba五.比一比比较(a+b)2=a2+2ab+b2及(a-b)2=a2-2ab+b2这两个公式有什么不同?有什么联系?归纳:首平方,末平方,首末2倍中间放左边是两数和(或差)的平方,右边是一个三项式,其中两项是这两数的平方,另一项是这两数积的2倍,右边三项中仅有中间一项符好相反 例1 计算
(1) (2a+3b)2 (3) (2x-3y)2
(2) (2a+ )2 (4) (-m+3n)2
六.举例及应用例2 如果多项式x2+kx+25是完全平方式,求k的值。解:设(x+m)2=x2+kx+25X2+2mx+m2=x2+kx+25 m2=25,k=2mm= 5,k= 10例3 已知a+b=5,ab=2,求下例各式的值
(1) a2+b2
(2) (a-b)2
(3) a2-ab+b2六.举例及应用解:(1)a2+b2=(a+b)2-2ab=52-2×2=21(2)(a-b)2=(a+b)2-4ab=52-2×4=17(3)a2-ab+b 2=(a+b)2-3ab=52-3×2=19例4 运用公式进行简便计算
(1) 1012 (2)19992
六.举例及应用解:(1)1012=(100+1)2=100 2+2×100×1+1=10201(2)19992=(2000-1)2=20002-2×2000×1+1=3996001说明:1、这两个公式是多项式乘法的特殊情况。
2、公式中字母可以是数也可以是单项式或 多项式。七、收获这节课你有那些收获?1、学会了由多项式乘法推导出完全平方公式。
2、了解两个公式的几何背景,感受生活中完全
平方公式的存在与意义。
3、学会了运用公式进行简便计算。
4、体会了乘法公式来源于整式的乘法,又应用于整式的乘法的辨证性。
再见
1(x+y)(x+y) =
x2+2xy+y2a2+4ab+4b20.25m2+2mn+n2做一做,并观察等式的左边和右边你发现有什么规律。2 (a+2b)(a+2b) =3 ( 0.5m+n)(0.5m+n) =2(2ab)(2b)2(0.5)22(0.5mn)二.拼一拼,算一算你能用一个边长为a的正方形和一个边长为b的正方形,及一个长为a宽为b的矩形拼出一个正方形吗?提问:你能用这个图形验证
(a+b)2=a2+2ab+b2吗?三.想一想你会用(a + b)2=a2+2ab+b2计算(a-b)2吗?解:(a-b)2=[a+(-b)]2两数差的平方:(a-b)2=a2-2ab+b2 =a2+2a(-b)+b2
=a2-2ab+b2四.实践与探索右图是用4个长为a、宽为b的矩形拼
成的正方形,中间留下的“洞”恰好是
一个小正方形,用不同的方法计算中
间小正方形的面积,你发现了什么?解:因为s小正方形=s大正方形 -4s矩形 故s小正方形=(a+b)2-4ab =a2+2ab+b2-4ab =a2-2ab+b2又有图可知小正方形的边长为(a-b),所以
S小正方形=(a-b)2所以(a-b)2=a2-2ab+b2ba五.比一比比较(a+b)2=a2+2ab+b2及(a-b)2=a2-2ab+b2这两个公式有什么不同?有什么联系?归纳:首平方,末平方,首末2倍中间放左边是两数和(或差)的平方,右边是一个三项式,其中两项是这两数的平方,另一项是这两数积的2倍,右边三项中仅有中间一项符好相反 例1 计算
(1) (2a+3b)2 (3) (2x-3y)2
(2) (2a+ )2 (4) (-m+3n)2
六.举例及应用例2 如果多项式x2+kx+25是完全平方式,求k的值。解:设(x+m)2=x2+kx+25X2+2mx+m2=x2+kx+25 m2=25,k=2mm= 5,k= 10例3 已知a+b=5,ab=2,求下例各式的值
(1) a2+b2
(2) (a-b)2
(3) a2-ab+b2六.举例及应用解:(1)a2+b2=(a+b)2-2ab=52-2×2=21(2)(a-b)2=(a+b)2-4ab=52-2×4=17(3)a2-ab+b 2=(a+b)2-3ab=52-3×2=19例4 运用公式进行简便计算
(1) 1012 (2)19992
六.举例及应用解:(1)1012=(100+1)2=100 2+2×100×1+1=10201(2)19992=(2000-1)2=20002-2×2000×1+1=3996001说明:1、这两个公式是多项式乘法的特殊情况。
2、公式中字母可以是数也可以是单项式或 多项式。七、收获这节课你有那些收获?1、学会了由多项式乘法推导出完全平方公式。
2、了解两个公式的几何背景,感受生活中完全
平方公式的存在与意义。
3、学会了运用公式进行简便计算。
4、体会了乘法公式来源于整式的乘法,又应用于整式的乘法的辨证性。
再见
