数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 07:10:19 | ||
图片预览





文档简介
(共20张PPT)
1.3.1 空间直角坐标系
1.3 空间向量及其运算的坐标表示
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
新知导入
问题1 类比平面向量直角坐标系,你能猜想如何构建空间直角坐标系吗?
探究新知
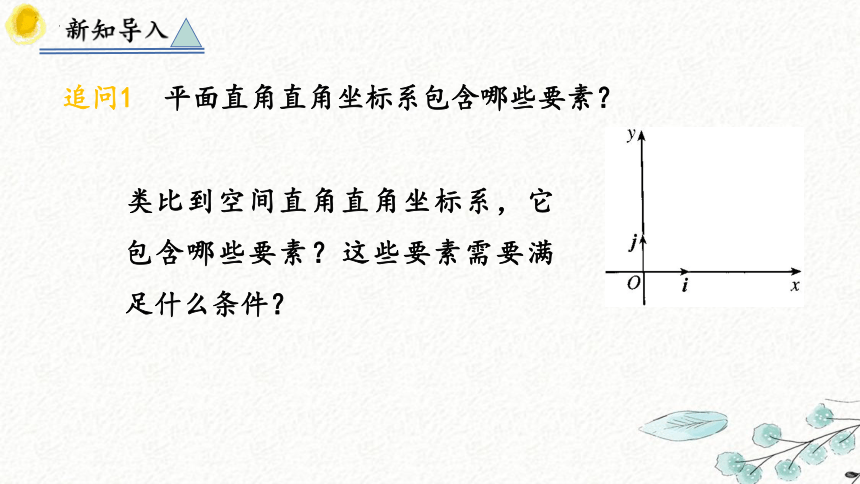
追问1 平面直角直角坐标系包含哪些要素?
类比到空间直角直角坐标系,它包含哪些要素?这些要素需要满足什么条件?
坐标系三要素 平面直角坐标系 空间直角坐标系
原点 坐标原点O 坐标原点O
坐标轴 互相垂直的两条坐标轴x轴和y轴 三条两两垂直的坐标轴
单位长度 单位长度 单位长度
探究新知
追问2 你能否给出空间直角坐标系的定义呢?
探究新知
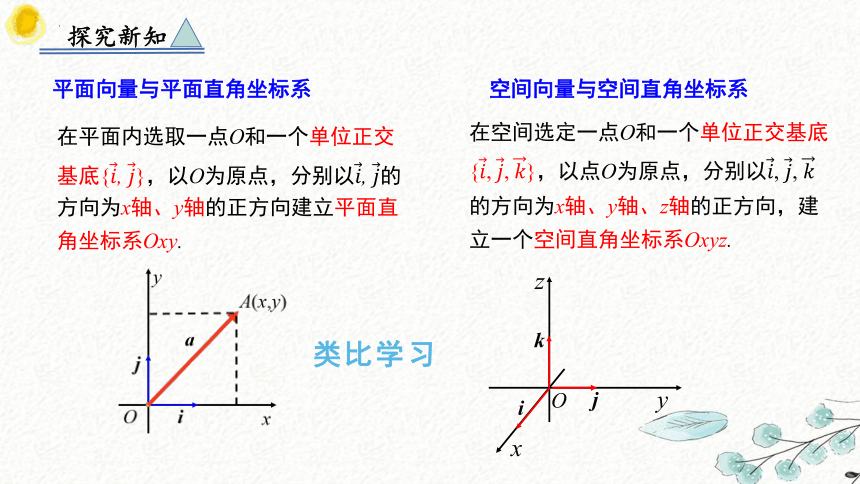
类比学面向量与平面直角坐标系
在平面内选取一点O和一个单位正交基底{, },以O为原点,分别以, 的方向为x轴、y轴的正方向建立平面直角坐标系Oxy.
空间向量与空间直角坐标系
在空间选定一点O和一个单位正交基底{,,},以点O为原点,分别以, , 的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系Oxyz.
x
y
z
i
j
k
O
探究新知
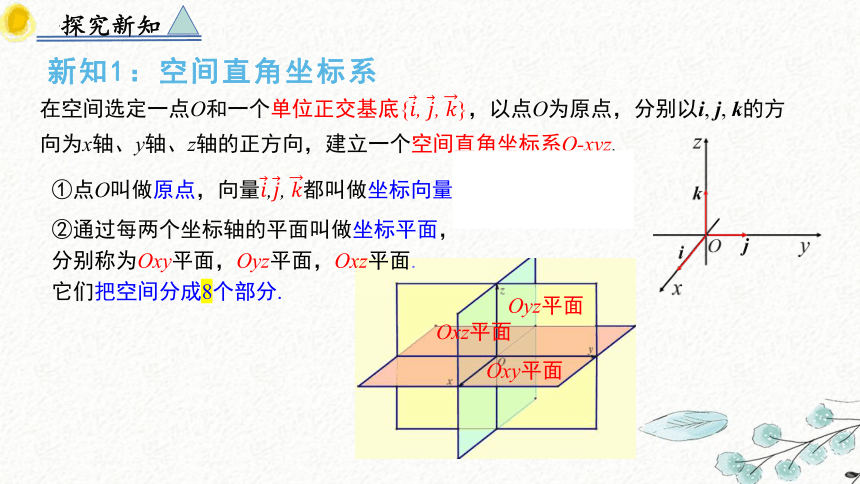
新知1:空间直角坐标系
在空间选定一点O和一个单位正交基底{, , },以点O为原点,分别以i, j, k的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系O-xyz.
||=||=||=1.
·=·=·=0
Oxy平面
Oyz平面
Oxz平面
①点O叫做原点,向量,, 都叫做坐标向量.
②通过每两个坐标轴的平面叫做坐标平面,
分别称为Oxy平面,Oyz平面,Oxz平面.
它们把空间分成8个部分.
探究新知
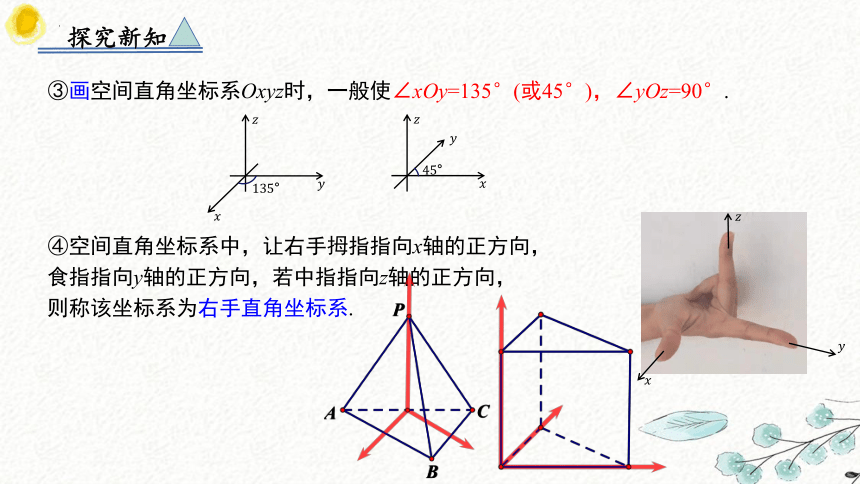
③画空间直角坐标系Oxyz时,一般使∠xOy=135(或45°),∠yOz=90°.
④空间直角坐标系中,让右手拇指指向x轴的正方向,
食指指向y轴的正方向,若中指指向z轴的正方向,
则称该坐标系为右手直角坐标系.
探究新知
思考 在平面直角坐标系中,每一个点和向量都可以用一对有
序实数对(即它的坐标)表示,在空间直角坐标系中是否
也有类似的表示?
探究新知
x
y
z
O
A(x,y,z)
i
j
k
新知2.1:空间点和向量的坐标
注意:(x, y, z)具有双重意义,既可以表示向量,也可以表示点,在表述时注意区分
新知2.1:空间点和向量的坐标
探究新知
新知2.1:空间点和向量的坐标
空间任意一点A对应一个,即点A的位置由唯一确定.
由空间向量基本定理,存在唯一的有序实数组(x, y, z),使=x+y+z.
空间点的坐标:在单位正交基底{, , }下,=x+y+z,则有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫横坐标,y叫纵坐标,z叫竖坐标.
空间向量的坐标:在空间直角坐标系Oxyz中,对空间任一向量,作=(如图), 由空间向量基本定理,存在唯一的有序实数组(x, y, z),使=x+y+z. 把有序实数组(x, y, z)叫做在空间直角坐标系Oxyz中的坐标,简记作=(x, y, z).
向量终点的坐标
A(x,y,z)
向量的坐标
OA=(x,y,z)
一一对应
3
6
2
A(6,3,2)
=(6,3,2)
以坐标原点O为起点的向量的坐标和终点A的坐标相同。
新知2.2:空间中的特殊点和对称点
点的位置 x轴上 y轴上 z轴上 xOy平面 xOz平面 yOz平面
点的坐标
(x, 0, 0)
(0, y, 0)
(0, 0, z)
(x, y, 0)
(x, 0, z)
(0, y, z)
已知点A(x , y , z) ,则:
①点A关于x轴对称的点为A1___________;
②点A关于y轴对称的点为A2___________;
③点A关于z轴对称的点为A3___________.
④点A关于原点对称的点为A4___________.
⑤点A关于Oxy平面对称的点为A5 __________;
⑥点A关于Oxz平面对称的点为A6 __________;
⑦点A关于Oyz平面对称的点为A7 __________.
(x , y , -z)
(-x , y , z)
(x , -y , z)
(x , -y , -z)
(-x , -y , z)
(-x , y , -z)
(-x , -y , -z)
规律:关于谁对称,谁就不变!其余互为相反数。
典例.在空间直角坐标系Oxyz中,
(1)坐标平面____与x轴垂直,坐标平面_____与y轴垂直,坐标平面____与z轴垂直;
(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标;
在Oyz平面内的射影坐标为____________
在Oxz平面内的射影坐标为____________
在Oxy平面内的射影坐标为____________
(3)点P(1,3,5)关于原点成中心对称的点的坐标是___________.
(4)点P(1,3,5)在x轴上的射影坐标为_________.
Oyz
Oxz
Oxy
(0,3,4)
(2,0,4)
(2,3,0)
(-1,-3,-5)
点在平面内的射影:过点作平面的垂线所得的垂足.
点在坐标轴的射影:过点作坐标轴的垂线所得的垂足.
(1,0,0)
规律:在坐标平面或坐标轴的射影坐标——缺谁谁就为0.
例题讲解
P18-例1. 如图,在长方体中OABC-O'A'B'C'中,OA=3,OC=4,OD'=2,
以{,,}为单位正交基底,建立如图所示的空间直角坐标系O.
(1)写出D',C,A',B'四点的坐标;
(2)写出向量,,的坐标.
分析:(1)D'(0, 0, 2)
C(0, 4, 0)
A'(3, 0, 2)
B'(3, 4, 2)
(2)==(0,4,0)
=-=(0,0,-2)
===(0,4,0)-(3,0,0)=(-3,4,0)
=+=(-3,0,0)+(0,4,0)+(0,0,2)=(-3,4,2)
(法1)利用向量的加减及数乘运算,将所求向量尽量用坐标平面内易知坐标的向量表示出来,从而确定该向量的坐标。
例题讲解
回顾本节课的学习过程,我们是如何得空间点和空间向量的坐标表示的?
课堂小结
如何求空间点或者向量的坐标呢?
课堂小结
THANKS
1.3.1 空间直角坐标系
1.3 空间向量及其运算的坐标表示
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
新知导入
问题1 类比平面向量直角坐标系,你能猜想如何构建空间直角坐标系吗?
探究新知
追问1 平面直角直角坐标系包含哪些要素?
类比到空间直角直角坐标系,它包含哪些要素?这些要素需要满足什么条件?
坐标系三要素 平面直角坐标系 空间直角坐标系
原点 坐标原点O 坐标原点O
坐标轴 互相垂直的两条坐标轴x轴和y轴 三条两两垂直的坐标轴
单位长度 单位长度 单位长度
探究新知
追问2 你能否给出空间直角坐标系的定义呢?
探究新知
类比学面向量与平面直角坐标系
在平面内选取一点O和一个单位正交基底{, },以O为原点,分别以, 的方向为x轴、y轴的正方向建立平面直角坐标系Oxy.
空间向量与空间直角坐标系
在空间选定一点O和一个单位正交基底{,,},以点O为原点,分别以, , 的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系Oxyz.
x
y
z
i
j
k
O
探究新知
新知1:空间直角坐标系
在空间选定一点O和一个单位正交基底{, , },以点O为原点,分别以i, j, k的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系O-xyz.
||=||=||=1.
·=·=·=0
Oxy平面
Oyz平面
Oxz平面
①点O叫做原点,向量,, 都叫做坐标向量.
②通过每两个坐标轴的平面叫做坐标平面,
分别称为Oxy平面,Oyz平面,Oxz平面.
它们把空间分成8个部分.
探究新知
③画空间直角坐标系Oxyz时,一般使∠xOy=135(或45°),∠yOz=90°.
④空间直角坐标系中,让右手拇指指向x轴的正方向,
食指指向y轴的正方向,若中指指向z轴的正方向,
则称该坐标系为右手直角坐标系.
探究新知
思考 在平面直角坐标系中,每一个点和向量都可以用一对有
序实数对(即它的坐标)表示,在空间直角坐标系中是否
也有类似的表示?
探究新知
x
y
z
O
A(x,y,z)
i
j
k
新知2.1:空间点和向量的坐标
注意:(x, y, z)具有双重意义,既可以表示向量,也可以表示点,在表述时注意区分
新知2.1:空间点和向量的坐标
探究新知
新知2.1:空间点和向量的坐标
空间任意一点A对应一个,即点A的位置由唯一确定.
由空间向量基本定理,存在唯一的有序实数组(x, y, z),使=x+y+z.
空间点的坐标:在单位正交基底{, , }下,=x+y+z,则有序实数组(x,y,z),叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫横坐标,y叫纵坐标,z叫竖坐标.
空间向量的坐标:在空间直角坐标系Oxyz中,对空间任一向量,作=(如图), 由空间向量基本定理,存在唯一的有序实数组(x, y, z),使=x+y+z. 把有序实数组(x, y, z)叫做在空间直角坐标系Oxyz中的坐标,简记作=(x, y, z).
向量终点的坐标
A(x,y,z)
向量的坐标
OA=(x,y,z)
一一对应
3
6
2
A(6,3,2)
=(6,3,2)
以坐标原点O为起点的向量的坐标和终点A的坐标相同。
新知2.2:空间中的特殊点和对称点
点的位置 x轴上 y轴上 z轴上 xOy平面 xOz平面 yOz平面
点的坐标
(x, 0, 0)
(0, y, 0)
(0, 0, z)
(x, y, 0)
(x, 0, z)
(0, y, z)
已知点A(x , y , z) ,则:
①点A关于x轴对称的点为A1___________;
②点A关于y轴对称的点为A2___________;
③点A关于z轴对称的点为A3___________.
④点A关于原点对称的点为A4___________.
⑤点A关于Oxy平面对称的点为A5 __________;
⑥点A关于Oxz平面对称的点为A6 __________;
⑦点A关于Oyz平面对称的点为A7 __________.
(x , y , -z)
(-x , y , z)
(x , -y , z)
(x , -y , -z)
(-x , -y , z)
(-x , y , -z)
(-x , -y , -z)
规律:关于谁对称,谁就不变!其余互为相反数。
典例.在空间直角坐标系Oxyz中,
(1)坐标平面____与x轴垂直,坐标平面_____与y轴垂直,坐标平面____与z轴垂直;
(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标;
在Oyz平面内的射影坐标为____________
在Oxz平面内的射影坐标为____________
在Oxy平面内的射影坐标为____________
(3)点P(1,3,5)关于原点成中心对称的点的坐标是___________.
(4)点P(1,3,5)在x轴上的射影坐标为_________.
Oyz
Oxz
Oxy
(0,3,4)
(2,0,4)
(2,3,0)
(-1,-3,-5)
点在平面内的射影:过点作平面的垂线所得的垂足.
点在坐标轴的射影:过点作坐标轴的垂线所得的垂足.
(1,0,0)
规律:在坐标平面或坐标轴的射影坐标——缺谁谁就为0.
例题讲解
P18-例1. 如图,在长方体中OABC-O'A'B'C'中,OA=3,OC=4,OD'=2,
以{,,}为单位正交基底,建立如图所示的空间直角坐标系O.
(1)写出D',C,A',B'四点的坐标;
(2)写出向量,,的坐标.
分析:(1)D'(0, 0, 2)
C(0, 4, 0)
A'(3, 0, 2)
B'(3, 4, 2)
(2)==(0,4,0)
=-=(0,0,-2)
===(0,4,0)-(3,0,0)=(-3,4,0)
=+=(-3,0,0)+(0,4,0)+(0,0,2)=(-3,4,2)
(法1)利用向量的加减及数乘运算,将所求向量尽量用坐标平面内易知坐标的向量表示出来,从而确定该向量的坐标。
例题讲解
回顾本节课的学习过程,我们是如何得空间点和空间向量的坐标表示的?
课堂小结
如何求空间点或者向量的坐标呢?
课堂小结
THANKS
