人教版四年级下册数学 《平均数》(表格式)教案
文档属性
| 名称 | 人教版四年级下册数学 《平均数》(表格式)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 373.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 07:52:54 | ||
图片预览

文档简介
课程基本信息
学科 数学 年级 四年级 学期 下册
课题 《平均数》
教科书 书 名: 义务教育教科书数学教材 出版社: 人民教育出版社 出版日期:2022年7月
核心素养目标
本单元属于统计与概率部分的内容,小学阶段在统计教学中主要培养儿童的数据意识,其表现在会用数学的语言表达现实世界。 数据意识主要是指对数据的意义和随机性的感悟。 1.知道在现实生活中,有许多问题应当先做调查研究,收集数据,感悟数据蕴含的信息; 2.知道同样的事情每次收集到的数据可能不同,而只要有足够的数据就可能从中发现规律; 3.知道同一组数据可以用不同方式表达,需要根据问题的背景选择合适的方式。 形成数据意识有助于理解生活中的随机现象,逐步养成用数据说话的习惯,进而到初中能产生数据观念、高中能达成数据分析的能力。
单元教学目标
1.经历收集、表示和分析数据的过程,认识条形统计图,能根据数据画出统计图,能根据条形统计图进行简单的分析、判断和预测; 2.了解平均数的意义,会求简单数据的平均数,能解决简单的实际问题; 3.进一步认识平均数,体会平均数的实际应用,感受数学与日常生活的密切联系; 4.经历收集数据、整理数据、分析数据的过程,体会统计在日常生活中的应用,积累统计活动的相关经验。
课时教学目标
1.用—个数表示—组数据的整体水平时,初步感受平均数产生的必要性; 2.会用移多补少、合并平分计算一组数据的平均数; 3.能用自己的语言解释平均数的意义,体会平均数的代表性、虚拟性、敏感性、区间性和公平性,会利用这些的特性解释生活中的平均数,感受数学与日常生活的密切联系。
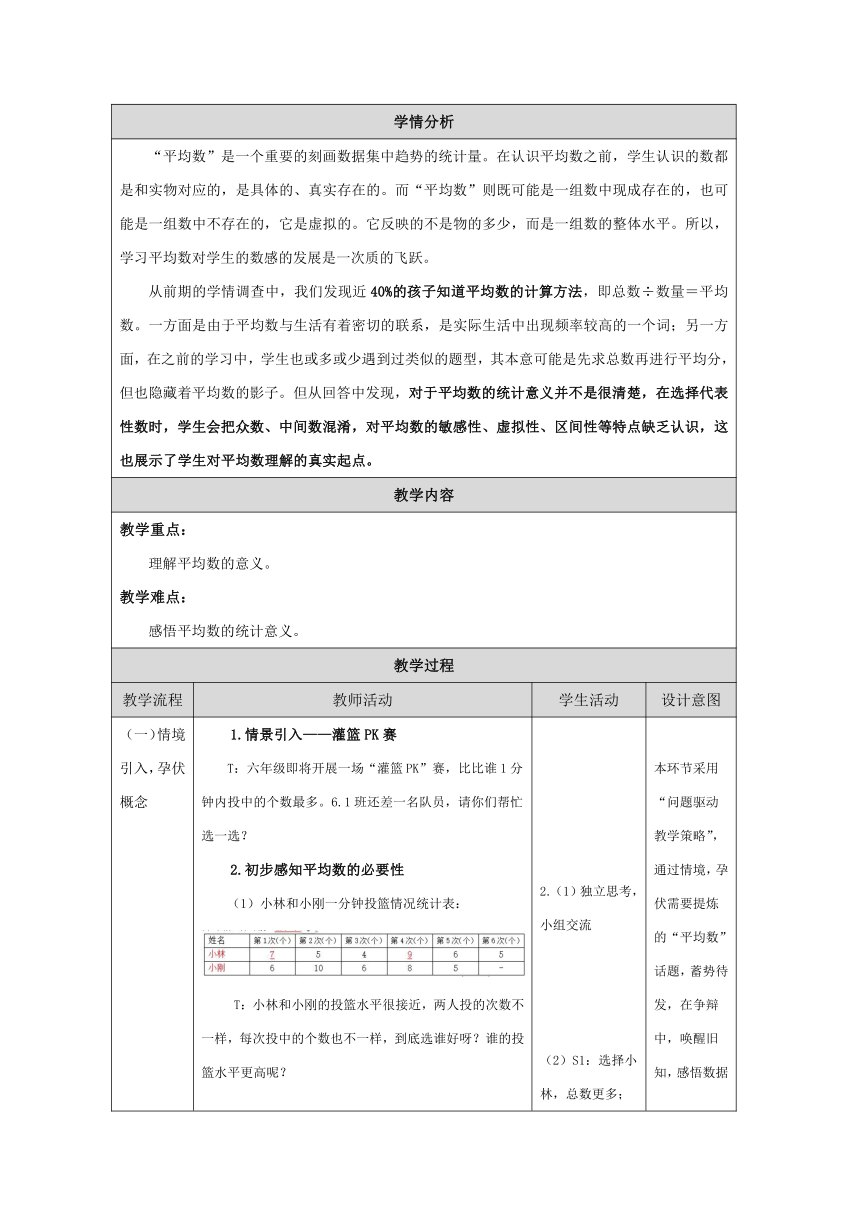
学情分析
“平均数”是一个重要的刻画数据集中趋势的统计量。在认识平均数之前,学生认识的数都是和实物对应的,是具体的、真实存在的。而“平均数”则既可能是一组数中现成存在的,也可能是一组数中不存在的,它是虚拟的。它反映的不是物的多少,而是一组数的整体水平。所以,学习平均数对学生的数感的发展是一次质的飞跃。 从前期的学情调查中,我们发现近40%的孩子知道平均数的计算方法,即总数÷数量=平均数。一方面是由于平均数与生活有着密切的联系,是实际生活中出现频率较高的一个词;另一方面,在之前的学习中,学生也或多或少遇到过类似的题型,其本意可能是先求总数再进行平均分,但也隐藏着平均数的影子。但从回答中发现,对于平均数的统计意义并不是很清楚,在选择代表性数时,学生会把众数、中间数混淆,对平均数的敏感性、虚拟性、区间性等特点缺乏认识,这也展示了学生对平均数理解的真实起点。
教学内容
教学重点: 理解平均数的意义。
教学难点: 感悟平均数的统计意义。
教学过程
教学流程 教师活动 学生活动 设计意图
(一)情境引入,孕伏概念 1.情景引入——灌篮PK赛 T:六年级即将开展一场“灌篮PK”赛,比比谁1分钟内投中的个数最多。6.1班还差一名队员,请你们帮忙选一选? 2.初步感知平均数的必要性 (1)小林和小刚一分钟投篮情况统计表: T:小林和小刚的投篮水平很接近,两人投的次数不一样,每次投中的个数也不一样,到底选谁好呀?谁的投篮水平更高呢? (2)说明选择理由。 3.引出“代表” 接下来,我们以小林的成绩为例,研究到底用哪个数据代表他投篮的整体水平,更合理? 2.(1)独立思考,小组交流 (2)S1:选择小林,总数更多; S2:选择小刚,平均数更多。 本环节采用“问题驱动教学策略”,通过情境,孕伏需要提炼的“平均数”话题,蓄势待发,在争辩中,唤醒旧知,感悟数据内容。
(二)逐步逼近,生成概念 1.理解平均数的算法和意义(代表性),感受平均数的虚拟性 活动一:找代表小林投篮的整体水平的数据 (1)T:找找你想用哪个数据代表小林投篮的整体水平?并说明你的理由。 (2)学生汇报,老师适时动画演示、板书。 T总结:都是在不改变原来总数的情况下进行平均分配,使每次的数据变成相同的6。 (3)出示概念 T:能代表一组数的整体水平的数就是“平均数”。 (4)再次理解平均数意义,感受虚拟性 T:这里相同的 6是真正的相同吗?也就是每一次的成绩都是6个吗? 总结:平均数并不是一个真实存在的数,而且匀出来的一个能代表整体水平的数,所以我们就说平均数具有虚拟的特点。 2.感受平均数的区间值和敏感性 活动二:找一找小刚这组成绩的平均数 (1)感受平均数的范围 T:猜一猜小刚的平均水平可能是在哪? (2)求小刚的平均成绩。 (3)再次感受平均数的虚拟性 T:可是一次都没有投出7,能用7来代表他的成绩吗? 3.感受平均数的公平性 T:你们认为谁能代表6.1班参加年级PK赛呢? 小结:这里的两组数据,个数不同,每次投的数据也不一样,这就需要找一个能代表整体水平的数,平均数恰好能满足这样的需求,所以用平均数比较,更合理,更公平。 4.丰富对平均数的理解,体会“敏感性” 活动三:再挑战一次 T:这时小刚想再挑战一次,这6次跟前5次相比,平均数会发生变化吗?怎么变呢? T总结:只要其中任意一个数发生改变,平均数就有可能发生变化,这样才能更好代表这组数的整体水平。平均数与每一个数都密切相关,一点风吹草地,它就有可能发生变化,所以它也非常的灵敏。 1.(1)独立思考结束后直接小组交流。 (2)S1:移多补少 S2:合并平分 S3:计算 (4)①虚拟性:意义不一样,它是通过变成一样的来找出他成绩的整体水平。 2.(1)S:平均数在最小和最大数之间 (2)移多补少; 计算。 (3)平均数7是匀出来的,第3次7是投出的具体个数,意义不一样。 3.S:通过刚刚的比较,发现小刚成绩更好 4.S:生白板演示水平线的移动——第6次=7(不变)、第6次<7(降低)、第6次>7(升高) 本环节采取数形结合的形式展现,通过三个层次的活动,让学生充分理解平均数的意义。“平均数”的代表性,有范围,虚拟性,敏感性,公平性属于一个不可切割的整体,相互联系 ,彼此依存。
(三)知识应用,深度思考 1.巩固练习,再次理解平均数的特性(判断) (1)王悦5次跳远的总成绩是10m,她每次的跳远成绩肯定都是2m。 (2)学校排球队队员的平均身高是160 cm,有的队员身高会超过160 cm,有的队员身高不到160 cm。 (3)小东所在小组同学的平均体重是36 kg,小刚所在小组同学的平均体重是34 kg,小东一定比小刚重。 2.生活中的平均数(初步发展数据意识) (1)生活中的平均数 T:生活中哪些地方你听说过平均数? (2)数学文化——平均数的由来 1.学生思考并说明理由 (1)× (2)√ (3)× 2.全班交流:平均分、平均水深、平均寿命平均温度、平均身高... 通过大量的生活情境,促进了学生理解平均数概念内涵,帮助学生积累数学思考和解决问题的经验,让经验驻足。
(四)课堂小结,梳理总结 1.全课总结 T:回头看,以前很多同学都听说了平均数、也会算平均数,通过这节课的学习,你对平均数有哪些新的认识? 2.课后延伸 T:关于平均数,你还有没有什么想对它说的? 1.生回顾 2.平均数这么有用?那它有没有缺点呢?
板书设计
学科 数学 年级 四年级 学期 下册
课题 《平均数》
教科书 书 名: 义务教育教科书数学教材 出版社: 人民教育出版社 出版日期:2022年7月
核心素养目标
本单元属于统计与概率部分的内容,小学阶段在统计教学中主要培养儿童的数据意识,其表现在会用数学的语言表达现实世界。 数据意识主要是指对数据的意义和随机性的感悟。 1.知道在现实生活中,有许多问题应当先做调查研究,收集数据,感悟数据蕴含的信息; 2.知道同样的事情每次收集到的数据可能不同,而只要有足够的数据就可能从中发现规律; 3.知道同一组数据可以用不同方式表达,需要根据问题的背景选择合适的方式。 形成数据意识有助于理解生活中的随机现象,逐步养成用数据说话的习惯,进而到初中能产生数据观念、高中能达成数据分析的能力。
单元教学目标
1.经历收集、表示和分析数据的过程,认识条形统计图,能根据数据画出统计图,能根据条形统计图进行简单的分析、判断和预测; 2.了解平均数的意义,会求简单数据的平均数,能解决简单的实际问题; 3.进一步认识平均数,体会平均数的实际应用,感受数学与日常生活的密切联系; 4.经历收集数据、整理数据、分析数据的过程,体会统计在日常生活中的应用,积累统计活动的相关经验。
课时教学目标
1.用—个数表示—组数据的整体水平时,初步感受平均数产生的必要性; 2.会用移多补少、合并平分计算一组数据的平均数; 3.能用自己的语言解释平均数的意义,体会平均数的代表性、虚拟性、敏感性、区间性和公平性,会利用这些的特性解释生活中的平均数,感受数学与日常生活的密切联系。
学情分析
“平均数”是一个重要的刻画数据集中趋势的统计量。在认识平均数之前,学生认识的数都是和实物对应的,是具体的、真实存在的。而“平均数”则既可能是一组数中现成存在的,也可能是一组数中不存在的,它是虚拟的。它反映的不是物的多少,而是一组数的整体水平。所以,学习平均数对学生的数感的发展是一次质的飞跃。 从前期的学情调查中,我们发现近40%的孩子知道平均数的计算方法,即总数÷数量=平均数。一方面是由于平均数与生活有着密切的联系,是实际生活中出现频率较高的一个词;另一方面,在之前的学习中,学生也或多或少遇到过类似的题型,其本意可能是先求总数再进行平均分,但也隐藏着平均数的影子。但从回答中发现,对于平均数的统计意义并不是很清楚,在选择代表性数时,学生会把众数、中间数混淆,对平均数的敏感性、虚拟性、区间性等特点缺乏认识,这也展示了学生对平均数理解的真实起点。
教学内容
教学重点: 理解平均数的意义。
教学难点: 感悟平均数的统计意义。
教学过程
教学流程 教师活动 学生活动 设计意图
(一)情境引入,孕伏概念 1.情景引入——灌篮PK赛 T:六年级即将开展一场“灌篮PK”赛,比比谁1分钟内投中的个数最多。6.1班还差一名队员,请你们帮忙选一选? 2.初步感知平均数的必要性 (1)小林和小刚一分钟投篮情况统计表: T:小林和小刚的投篮水平很接近,两人投的次数不一样,每次投中的个数也不一样,到底选谁好呀?谁的投篮水平更高呢? (2)说明选择理由。 3.引出“代表” 接下来,我们以小林的成绩为例,研究到底用哪个数据代表他投篮的整体水平,更合理? 2.(1)独立思考,小组交流 (2)S1:选择小林,总数更多; S2:选择小刚,平均数更多。 本环节采用“问题驱动教学策略”,通过情境,孕伏需要提炼的“平均数”话题,蓄势待发,在争辩中,唤醒旧知,感悟数据内容。
(二)逐步逼近,生成概念 1.理解平均数的算法和意义(代表性),感受平均数的虚拟性 活动一:找代表小林投篮的整体水平的数据 (1)T:找找你想用哪个数据代表小林投篮的整体水平?并说明你的理由。 (2)学生汇报,老师适时动画演示、板书。 T总结:都是在不改变原来总数的情况下进行平均分配,使每次的数据变成相同的6。 (3)出示概念 T:能代表一组数的整体水平的数就是“平均数”。 (4)再次理解平均数意义,感受虚拟性 T:这里相同的 6是真正的相同吗?也就是每一次的成绩都是6个吗? 总结:平均数并不是一个真实存在的数,而且匀出来的一个能代表整体水平的数,所以我们就说平均数具有虚拟的特点。 2.感受平均数的区间值和敏感性 活动二:找一找小刚这组成绩的平均数 (1)感受平均数的范围 T:猜一猜小刚的平均水平可能是在哪? (2)求小刚的平均成绩。 (3)再次感受平均数的虚拟性 T:可是一次都没有投出7,能用7来代表他的成绩吗? 3.感受平均数的公平性 T:你们认为谁能代表6.1班参加年级PK赛呢? 小结:这里的两组数据,个数不同,每次投的数据也不一样,这就需要找一个能代表整体水平的数,平均数恰好能满足这样的需求,所以用平均数比较,更合理,更公平。 4.丰富对平均数的理解,体会“敏感性” 活动三:再挑战一次 T:这时小刚想再挑战一次,这6次跟前5次相比,平均数会发生变化吗?怎么变呢? T总结:只要其中任意一个数发生改变,平均数就有可能发生变化,这样才能更好代表这组数的整体水平。平均数与每一个数都密切相关,一点风吹草地,它就有可能发生变化,所以它也非常的灵敏。 1.(1)独立思考结束后直接小组交流。 (2)S1:移多补少 S2:合并平分 S3:计算 (4)①虚拟性:意义不一样,它是通过变成一样的来找出他成绩的整体水平。 2.(1)S:平均数在最小和最大数之间 (2)移多补少; 计算。 (3)平均数7是匀出来的,第3次7是投出的具体个数,意义不一样。 3.S:通过刚刚的比较,发现小刚成绩更好 4.S:生白板演示水平线的移动——第6次=7(不变)、第6次<7(降低)、第6次>7(升高) 本环节采取数形结合的形式展现,通过三个层次的活动,让学生充分理解平均数的意义。“平均数”的代表性,有范围,虚拟性,敏感性,公平性属于一个不可切割的整体,相互联系 ,彼此依存。
(三)知识应用,深度思考 1.巩固练习,再次理解平均数的特性(判断) (1)王悦5次跳远的总成绩是10m,她每次的跳远成绩肯定都是2m。 (2)学校排球队队员的平均身高是160 cm,有的队员身高会超过160 cm,有的队员身高不到160 cm。 (3)小东所在小组同学的平均体重是36 kg,小刚所在小组同学的平均体重是34 kg,小东一定比小刚重。 2.生活中的平均数(初步发展数据意识) (1)生活中的平均数 T:生活中哪些地方你听说过平均数? (2)数学文化——平均数的由来 1.学生思考并说明理由 (1)× (2)√ (3)× 2.全班交流:平均分、平均水深、平均寿命平均温度、平均身高... 通过大量的生活情境,促进了学生理解平均数概念内涵,帮助学生积累数学思考和解决问题的经验,让经验驻足。
(四)课堂小结,梳理总结 1.全课总结 T:回头看,以前很多同学都听说了平均数、也会算平均数,通过这节课的学习,你对平均数有哪些新的认识? 2.课后延伸 T:关于平均数,你还有没有什么想对它说的? 1.生回顾 2.平均数这么有用?那它有没有缺点呢?
板书设计
