人教版数学八年级上册 12.3.1 角的平分线的性质课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.3.1 角的平分线的性质课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
12.3.1 角的平分线的性质
1. 学会角平分线的画法.
2. 探究并认知角平分线的性质.
3. 熟练地运用角平分线的性质解决实际问题.
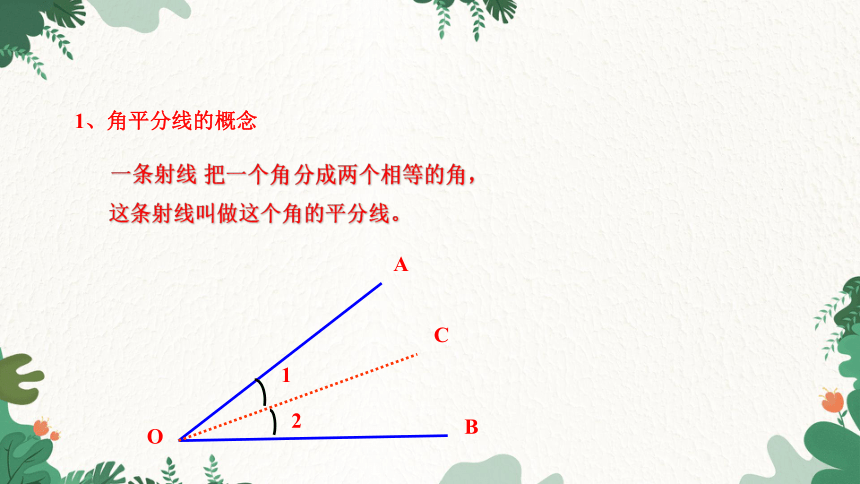
1、角平分线的概念
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
O
B
C
A
1
2
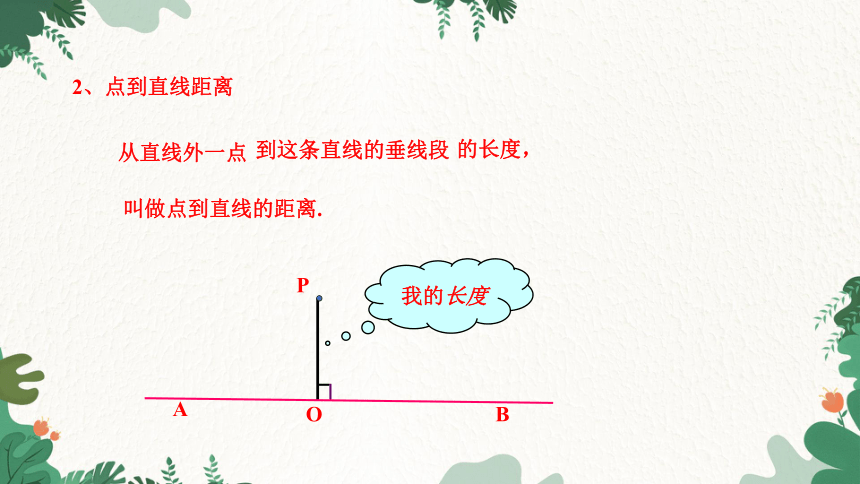
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离.
O
P
A
B
我的长度
2、点到直线距离
在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
如果把前面的纸片换成木板、钢板等,还能用对折的方法得到
木板、钢板的角平分线吗?
新知一 角平分线的画法
问题1:
问题2:
提炼图形
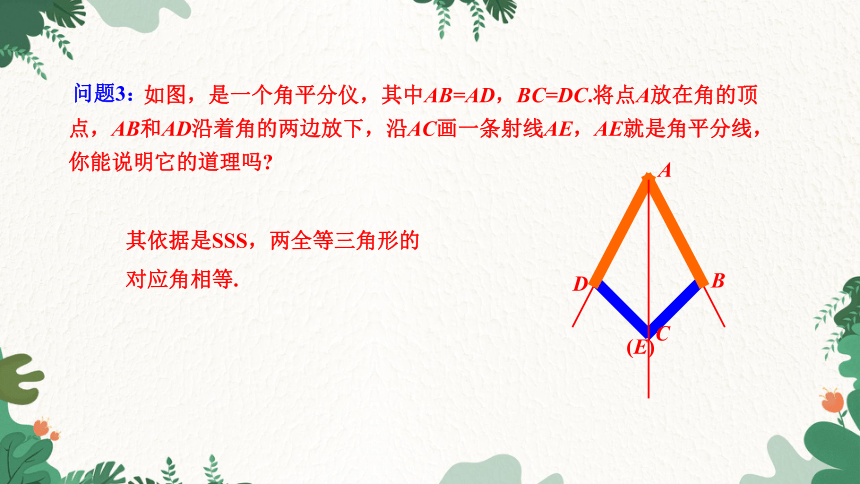
如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
B
C
(E)
D
其依据是SSS,两全等三角形的
对应角相等.
问题3:
如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗?
A
B
O
请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.
提示
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
A
B
M
N
C
O
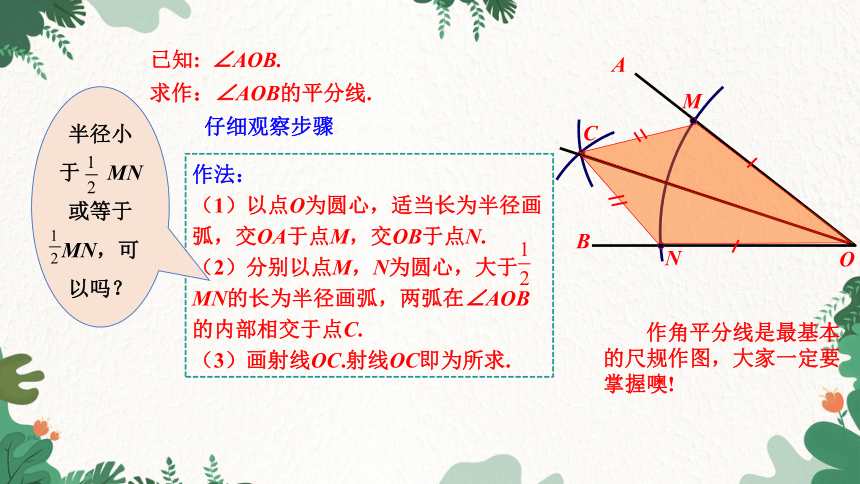
已知: ∠AOB.
求作:∠AOB的平分线.
仔细观察步骤
作角平分线是最基本的尺规作图,大家一定要掌握噢!
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
半径小于 MN或等于 MN,可以吗?
已知:平角∠AOB.
求作:平角∠AOB的角平分线.
结论:作平角的平分线的方法就是过直线上一点作这条直线的垂线的方法.
A
B
O
C
猜想:角的平分线上的点到角的两边的距离相等.
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE⊥OB ,点D,E为垂足,测量PD,PE的长.将三次数据填入下表:
2. 观察测量结果,猜想线段PD与PE的大小关系,写出结果:__________
PD PE
第一次
第二次
第三次
C
O
B
A
PD=PE
P
D
E
OC是∠AOB的平分线,点P是射线OC上的任意一点.
新知二 角平分线的性质
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.
角的平分线上的点到角的两边的距离相等.
性质定理:角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
应用格式:
∵OP 是∠AOB的平分线,
∴PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA, PE⊥OB,
B
A
D
O
P
E
C
例1 已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
例2 如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D,E,PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
提示:存在两条垂线段——直接 应用.
2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .
60
BF
E
B
D
F
A
C
G
3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
SSS
ASA
AAS
角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
4.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A . PC=PD B. OC=OD
C. ∠CPO=∠DPO D. OC=PC
D
5. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6 B.5 C.4 D.3
D
B
C
E
A
D
F
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
为证明线段相等提供了又一途径
谢谢大家!
12.3.1 角的平分线的性质
1. 学会角平分线的画法.
2. 探究并认知角平分线的性质.
3. 熟练地运用角平分线的性质解决实际问题.
1、角平分线的概念
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
O
B
C
A
1
2
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离.
O
P
A
B
我的长度
2、点到直线距离
在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
如果把前面的纸片换成木板、钢板等,还能用对折的方法得到
木板、钢板的角平分线吗?
新知一 角平分线的画法
问题1:
问题2:
提炼图形
如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
B
C
(E)
D
其依据是SSS,两全等三角形的
对应角相等.
问题3:
如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗?
A
B
O
请大家找到用尺规作角的平分线的方法,并说明作图方法与仪器的关系.
提示
(1)已知什么?求作什么?
(2)把平分角的仪器放在角的两边,仪器的顶点与角的顶点重合,且仪器的两边相等,怎样在作图中体现这个过程呢
(3)在平分角的仪器中,BC=DC,怎样在作图中体现这个过程呢?
(4)你能说明为什么OC是∠AOB的平分线吗?
A
B
M
N
C
O
已知: ∠AOB.
求作:∠AOB的平分线.
仔细观察步骤
作角平分线是最基本的尺规作图,大家一定要掌握噢!
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
半径小于 MN或等于 MN,可以吗?
已知:平角∠AOB.
求作:平角∠AOB的角平分线.
结论:作平角的平分线的方法就是过直线上一点作这条直线的垂线的方法.
A
B
O
C
猜想:角的平分线上的点到角的两边的距离相等.
1. 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE⊥OB ,点D,E为垂足,测量PD,PE的长.将三次数据填入下表:
2. 观察测量结果,猜想线段PD与PE的大小关系,写出结果:__________
PD PE
第一次
第二次
第三次
C
O
B
A
PD=PE
P
D
E
OC是∠AOB的平分线,点P是射线OC上的任意一点.
新知二 角平分线的性质
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.
角的平分线上的点到角的两边的距离相等.
性质定理:角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
应用格式:
∵OP 是∠AOB的平分线,
∴PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA, PE⊥OB,
B
A
D
O
P
E
C
例1 已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB,DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
例2 如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D,E,PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
提示:存在两条垂线段——直接 应用.
2.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
1. 如图,DE⊥AB,DF⊥BG,垂足分别是E,F, DE =DF, ∠EDB= 60°,则 ∠EBF= 度,BE= .
60
BF
E
B
D
F
A
C
G
3. 用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
SSS
ASA
AAS
角平分线上的点到角两边的距离相等
A
B
M
N
C
O
A
4.如图,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C,D,下列结论中错误的是( )
A . PC=PD B. OC=OD
C. ∠CPO=∠DPO D. OC=PC
D
5. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6 B.5 C.4 D.3
D
B
C
E
A
D
F
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
为证明线段相等提供了又一途径
谢谢大家!
