青岛版数学七年级上册 7.2一元一次方程课件(共19张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 7.2一元一次方程课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 19:41:45 | ||
图片预览





文档简介
(共20张PPT)
第7章 一元一次方程
7.2 一元一次方程
1.了解方程的解及解方程的意义,会判断一个数是不是某方程的解。
2.了解一元一次方程的意义,会识别一元一次方程。
学习目标
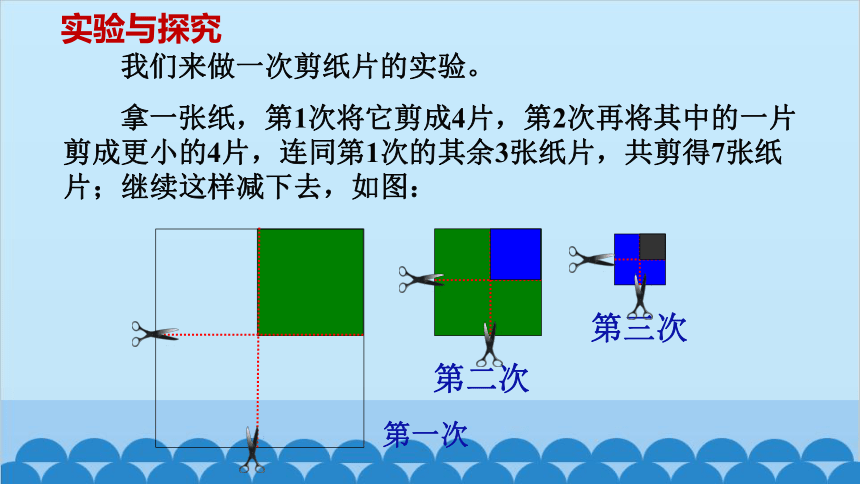
我们来做一次剪纸片的实验。
拿一张纸,第1次将它剪成4片,第2次再将其中的一片剪成更小的4片,连同第1次的其余3张纸片,共剪得7张纸片;继续这样减下去,如图:
第一次
第二次
第三次
实验与探究
次数 1 2 3 4 5 …
纸片数
10
13
16
…
4
7
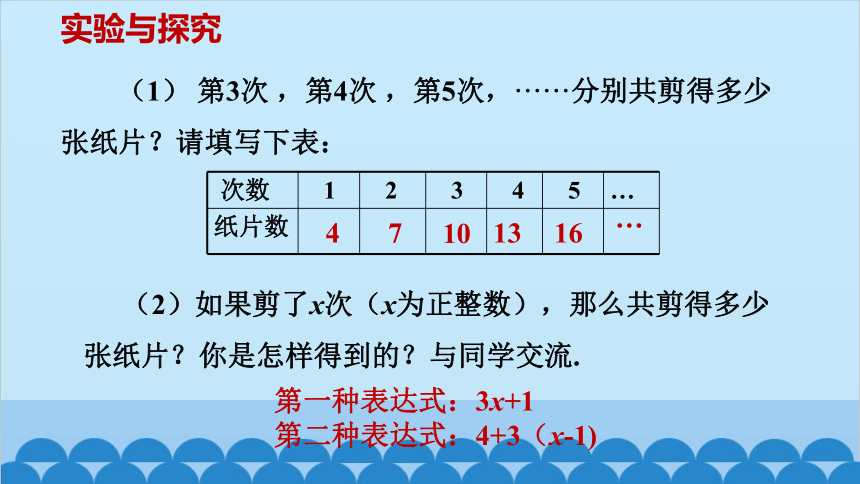
(1) 第3次 ,第4次 ,第5次,······分别共剪得多少张纸片?请填写下表:
(2)如果剪了x次(x为正整数),那么共剪得多少张纸片?你是怎样得到的?与同学交流.
第一种表达式:3x+1
第二种表达式:4+3(x-1)
实验与探究
(3)如果剪得的纸片共64片,一共剪了多少次?
3x+1=64
此时剪纸的次数x是未知数,问题中包含的等量关系是:
剪x次共剪得的纸片数=64.
4+3(x-1)=64
可得等式:
实验与探究
像这样含有未知数的等式叫做方程。
方程的定义:
(1)3x+1=64 (2)4+3(x-1)=64
(3)3x+5=2 (4)2x-3=x
方程是解决实际问题的重要工具!
归纳
判断下列各式是不是方程,并说明原因。
(1)-2+5=3 ( ) (2) 3χ-1=7 ( )
(3) m=0 ( ) (4) χ﹥ 3 ( )
(5)χ+y=8 ( ) (6)2χ2-5χ+1=0( )
(7) 2a +b ( ) (8)x=4 ( )
√
×
√
√
√
√
×
×
练习
1、使方程的两边相等的未知数的值叫做方程的解。
2、只含有一个未知数的方程的解也叫作方程的根。
3、求方程的解的过程叫做解方程。
1、什么叫方程的解?
2、什么叫解方程?
教材第156页相关概念:
自主探究
2.把x=3代入方程左边,结果等于多少?把x=2代入方程右边,结果等于多少 它们相等吗?
3.根据方程的解的定义,我们知道哪个数是方程的解?
4.讨论:检验一个数是不是方程的解的步骤。
例: x=1和x=3中哪个是方程2x-2=x+1的解
x 1 3
2x-2
x+1
0
2
4
4
1.把x=1代入方程左边,结果等于多少?把x=1代入方程右边,结果等于多少 它们相等吗
经典例题
检验一个数值是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
总结
1.请你判断下列给定的t的值中,哪个是方程2t+1=7-t的解?
(1 )t=-2 (2) t=2 (3)t=1
2.若 是方程 的解,则 =( )
1
练习
一元一次方程
这些方程之间有什么共同的特点?
一元一次方程
两边都是整式
只含有一个未知数
未知数的次数是一次
方程
总结
①、等号两边是不是整式
②、只含有一个未知数,且未知数的最高项次数为1
③、含未知数的项的系数不能都为0
一元一次方程
条件缺一不可。
判断方程是不是一元一次方程:
总结
1.下列各式中,哪些是方程,哪些是一元一次方程?
(1)、(3)、(4)、(5)、(6)是方程,只有(1)是一元一次方程。
练习
1) 是一元一次方程,则k=___
2) 是一元一次方程,则k=____
3) 是一元一次方程,则k=___.
4) 是一元一次方程,则k =___.
2
1或-1
-1
-2
2.计算并填空
练习
你能估算方程4+3(x-1)=64的解吗?
估计的x的值 左边(剪x次得到的纸片数) 与方程右边64比较
第一次估算
第二次估算
第三次估算
第四次估算
…… …… …… ……
10
25
20
22
31
76
61
67
小了
大了
小了
大了
知道如何选择估计值并进行估算了吗?对这种“估计-体验”的方法有什么体会?”
交流与发现
1.下列方程是一元一次方程的是( )
A 2x-1=0 B 2x-y=3
C x2-16=0 D 4(x-1)=2(3y+1)
2. 已知 ,是关于x的一元一次方程, 那么m=_________.
A
-1
练习
3.在以下方程后面的括号中找出方程的解
(1)8y+4=6(y+1), ( y= 1 ,y= 0 ),解是 y= ;
(2)x-2 x -3=0 , (x = 1 , x =- 3),解是 x = ;
4.根据题意列方程:
某班学生为灾区共捐款131元,比每人平均2元还多出35元,设这个班的学生有x人,根据题意列方程 _____________。
2x+35=131
1
-3
练习
1.方程及一元一次方程的概念;
2.方程的解以及检验一个未知数的值是不是方程的解的方法;
3.什么是解方程.
课堂小结
第7章 一元一次方程
7.2 一元一次方程
1.了解方程的解及解方程的意义,会判断一个数是不是某方程的解。
2.了解一元一次方程的意义,会识别一元一次方程。
学习目标
我们来做一次剪纸片的实验。
拿一张纸,第1次将它剪成4片,第2次再将其中的一片剪成更小的4片,连同第1次的其余3张纸片,共剪得7张纸片;继续这样减下去,如图:
第一次
第二次
第三次
实验与探究
次数 1 2 3 4 5 …
纸片数
10
13
16
…
4
7
(1) 第3次 ,第4次 ,第5次,······分别共剪得多少张纸片?请填写下表:
(2)如果剪了x次(x为正整数),那么共剪得多少张纸片?你是怎样得到的?与同学交流.
第一种表达式:3x+1
第二种表达式:4+3(x-1)
实验与探究
(3)如果剪得的纸片共64片,一共剪了多少次?
3x+1=64
此时剪纸的次数x是未知数,问题中包含的等量关系是:
剪x次共剪得的纸片数=64.
4+3(x-1)=64
可得等式:
实验与探究
像这样含有未知数的等式叫做方程。
方程的定义:
(1)3x+1=64 (2)4+3(x-1)=64
(3)3x+5=2 (4)2x-3=x
方程是解决实际问题的重要工具!
归纳
判断下列各式是不是方程,并说明原因。
(1)-2+5=3 ( ) (2) 3χ-1=7 ( )
(3) m=0 ( ) (4) χ﹥ 3 ( )
(5)χ+y=8 ( ) (6)2χ2-5χ+1=0( )
(7) 2a +b ( ) (8)x=4 ( )
√
×
√
√
√
√
×
×
练习
1、使方程的两边相等的未知数的值叫做方程的解。
2、只含有一个未知数的方程的解也叫作方程的根。
3、求方程的解的过程叫做解方程。
1、什么叫方程的解?
2、什么叫解方程?
教材第156页相关概念:
自主探究
2.把x=3代入方程左边,结果等于多少?把x=2代入方程右边,结果等于多少 它们相等吗?
3.根据方程的解的定义,我们知道哪个数是方程的解?
4.讨论:检验一个数是不是方程的解的步骤。
例: x=1和x=3中哪个是方程2x-2=x+1的解
x 1 3
2x-2
x+1
0
2
4
4
1.把x=1代入方程左边,结果等于多少?把x=1代入方程右边,结果等于多少 它们相等吗
经典例题
检验一个数值是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
总结
1.请你判断下列给定的t的值中,哪个是方程2t+1=7-t的解?
(1 )t=-2 (2) t=2 (3)t=1
2.若 是方程 的解,则 =( )
1
练习
一元一次方程
这些方程之间有什么共同的特点?
一元一次方程
两边都是整式
只含有一个未知数
未知数的次数是一次
方程
总结
①、等号两边是不是整式
②、只含有一个未知数,且未知数的最高项次数为1
③、含未知数的项的系数不能都为0
一元一次方程
条件缺一不可。
判断方程是不是一元一次方程:
总结
1.下列各式中,哪些是方程,哪些是一元一次方程?
(1)、(3)、(4)、(5)、(6)是方程,只有(1)是一元一次方程。
练习
1) 是一元一次方程,则k=___
2) 是一元一次方程,则k=____
3) 是一元一次方程,则k=___.
4) 是一元一次方程,则k =___.
2
1或-1
-1
-2
2.计算并填空
练习
你能估算方程4+3(x-1)=64的解吗?
估计的x的值 左边(剪x次得到的纸片数) 与方程右边64比较
第一次估算
第二次估算
第三次估算
第四次估算
…… …… …… ……
10
25
20
22
31
76
61
67
小了
大了
小了
大了
知道如何选择估计值并进行估算了吗?对这种“估计-体验”的方法有什么体会?”
交流与发现
1.下列方程是一元一次方程的是( )
A 2x-1=0 B 2x-y=3
C x2-16=0 D 4(x-1)=2(3y+1)
2. 已知 ,是关于x的一元一次方程, 那么m=_________.
A
-1
练习
3.在以下方程后面的括号中找出方程的解
(1)8y+4=6(y+1), ( y= 1 ,y= 0 ),解是 y= ;
(2)x-2 x -3=0 , (x = 1 , x =- 3),解是 x = ;
4.根据题意列方程:
某班学生为灾区共捐款131元,比每人平均2元还多出35元,设这个班的学生有x人,根据题意列方程 _____________。
2x+35=131
1
-3
练习
1.方程及一元一次方程的概念;
2.方程的解以及检验一个未知数的值是不是方程的解的方法;
3.什么是解方程.
课堂小结
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
