初中数学华师大版七年级上4.3立体图形的表面展开图 课件 (共16张PPT)
文档属性
| 名称 | 初中数学华师大版七年级上4.3立体图形的表面展开图 课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 20:36:07 | ||
图片预览




文档简介
(共16张PPT)
4.3立体图形的表面展开图
初中数学华师大版七上第四章图形的初步认识
温故而知新
1.你学过哪些立体图形?
2.圆柱的侧面展开图是一个什么图形?
长方形或正方形
创设情境
1.如图,在油桶下方的小壁虎要吃到油桶上方的蚊子,怎么走就最近?
蚊子
壁虎
油桶是个立体图形,要斜着上去,那就是要把油桶的侧面展开
壁虎
蚊子
2.生活中,常常遇到这样需要把整个立体图形的侧面展开。比如,要包装一个长方体礼物,我们就要根据它的表面展开图来剪包装纸.
1.自主思考,实践操作:
请你认真观察,想象,思考,有困难时动手画一画,折一折,再回答下列问题:
探究新知
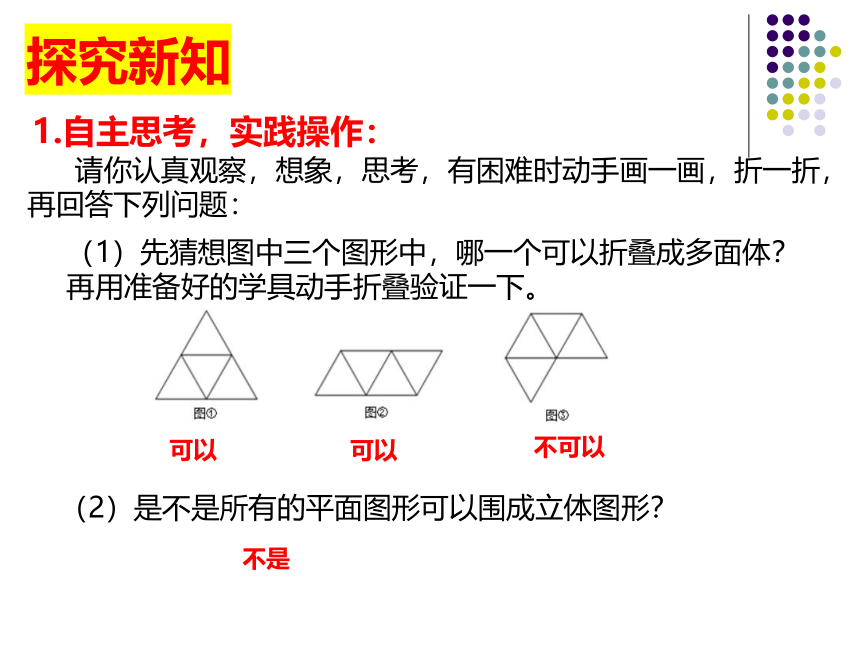
(1)先猜想图中三个图形中,哪一个可以折叠成多面体?再用准备好的学具动手折叠验证一下。
(2)是不是所有的平面图形可以围成立体图形?
可以
可以
不可以
不是
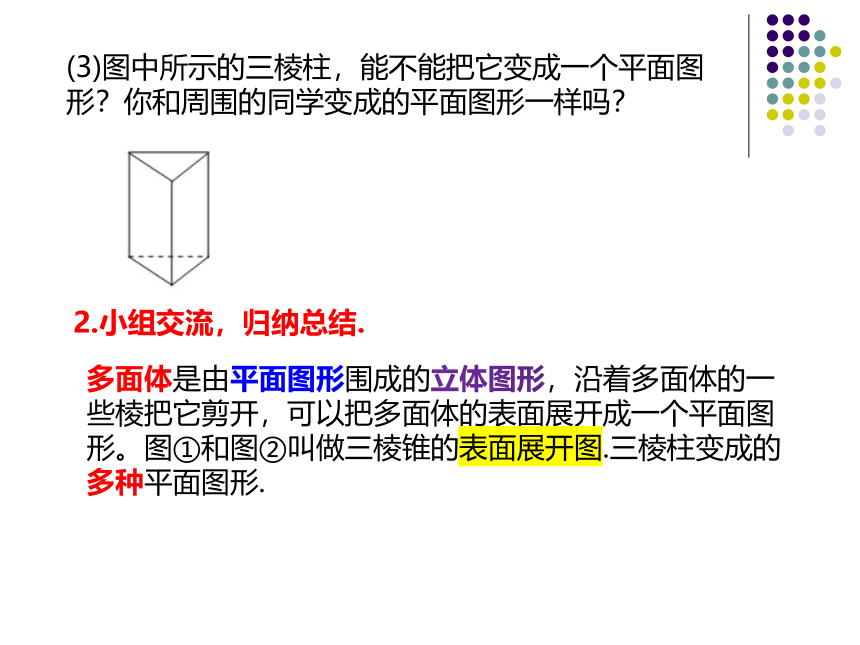
(3)图中所示的三棱柱,能不能把它变成一个平面图形?你和周围的同学变成的平面图形一样吗?
2.小组交流,归纳总结.
多面体是由平面图形围成的立体图形,沿着多面体的一些棱把它剪开,可以把多面体的表面展开成一个平面图形。图①和图②叫做三棱锥的表面展开图.三棱柱变成的多种平面图形.
3.继续探究:
①想一想:为什么同一个三棱锥、三棱柱有不同的展开图?其它立体图形的展开图是不是唯一的?
② 小结:同一个立体图形按不同的方式展开,得到的表面展开图不一样。其它立体图形的展开图不是唯一的.
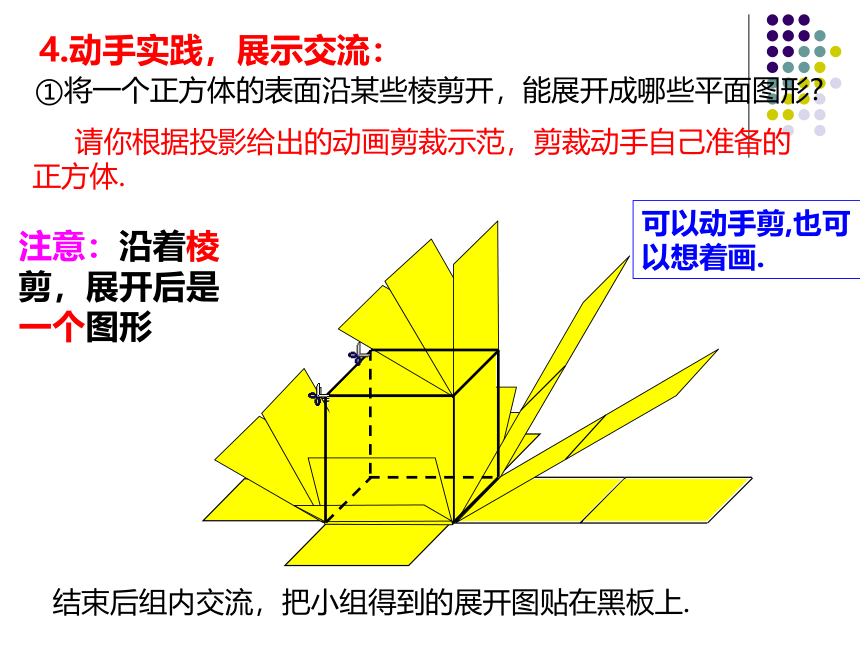
注意:沿着棱剪,展开后是一个图形
可以动手剪,也可以想着画.
4.动手实践,展示交流:
①将一个正方体的表面沿某些棱剪开,能展开成哪些平面图形?
请你根据投影给出的动画剪裁示范,剪裁动手自己准备的正方体.
结束后组内交流,把小组得到的展开图贴在黑板上.
②认真观察,黑板上的展开图有没有重复的?
认真观察分析,把重复的拿下来.
③你认为黑板上的哪几个可以归为一类?为什么归为一类?
④除了黑板上展示的展开图,还有没有其他展开图
5.深入探究,寻找规律
①认真观察老师补充之后的投影上面的11种正方体的展开图有没有什么规律?
蓝
黄
②小组讨论:这些正方体展开图可以分为几类?哪几号展开图可以分为一类,为什么?
③观察立方体相对的两个面在其展开图中的位置有什么特点?
相对的两个面不相连,上下隔一行,左右隔一列
例1请根据表面展开图说出立体图形的名称.
精讲例题
1.精讲例1
分析:表面展开图中,含有三角形时,考虑棱锥或者棱柱;如果只有两个三角形,一定是三棱柱;如果全是长方形,考虑四棱柱,如果全是正方形,一定是正方体;如果含有圆,考虑圆锥或者圆柱.
长方体
四棱锥
圆锥体
圆柱体
三棱柱
正方体
例2如图,若要使图中平面展开图折叠成正方体后,相对的面上的两个数互为相反数,则填入正方形内的三个数x、y、z依次为( )
3.精讲例2
分析:根据正方体表面展开图的特征判断“对面”,再根据相对的面上的两个数互为相反数求出答案即可.
A
A.-2,-3,-1 B.-3,2-1 C.2,-3,-1 D.2,-1,-3
掌握正方体表面展开图的特征、相反数的定义是正确解答的前提
3.精讲例3:
例3如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
解:设展开图的长方形的长为a,宽为b,由图可得:
12=3b,2b+a=22,解得a=14,b=4,
∴长方体的体积为:4×4×14=224,故选:B.
分析:根据展开图,可以求得原来长方体的底面的边长和高,然后根据长方体的体积公式计算即可.
温馨提示:本题考查几何体的展开图的计算应用,解答本题型的关键是明确展示图中对应立体图形的量的大小,利用数形结合的思想解答.
A.144 B.224 C.264 D.300
1、下面的图形那些是立方体的展开图?
课堂练习
长方体
2.如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面中与“一”相对的是( )
三棱柱
A
A.一 B.起 C.来 D.!
正方体
四棱锥
3.如图是一个长方体纸盒的展开图,则这个纸盒的体积是 .
(单位:cm3)
24 cm3
4.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是 ;
(2)求该几何体的表面积(结果保留π);
(3)求该几何体的体积(结果保留π).
4解:(1)该几何体的名称是圆柱,
(2)该几何体的表面积为:2π×22+5×4π=28π;
(3)该几何体的体积为:π×22×5=20π.
空间想像能力
动手操作能力
合作探究能力
课堂总结
立体图形
平面图形
立体图形的表面展开图
①有的立体图形是由平面图形围成的
②不是所有平面图形都可以围成为立体图形
③同一个立体图形按不同的方式展开,得到的表面展开图不一样
④正方体的11种表面展开图→相对的面
布置作业
1.是不是所有的平面图形都可以围成立体图形,是不是所有的立体图形都可展开成平面图形?
2.P131-132页1-3题
3.习题4.3的1-3题.
4.3立体图形的表面展开图
初中数学华师大版七上第四章图形的初步认识
温故而知新
1.你学过哪些立体图形?
2.圆柱的侧面展开图是一个什么图形?
长方形或正方形
创设情境
1.如图,在油桶下方的小壁虎要吃到油桶上方的蚊子,怎么走就最近?
蚊子
壁虎
油桶是个立体图形,要斜着上去,那就是要把油桶的侧面展开
壁虎
蚊子
2.生活中,常常遇到这样需要把整个立体图形的侧面展开。比如,要包装一个长方体礼物,我们就要根据它的表面展开图来剪包装纸.
1.自主思考,实践操作:
请你认真观察,想象,思考,有困难时动手画一画,折一折,再回答下列问题:
探究新知
(1)先猜想图中三个图形中,哪一个可以折叠成多面体?再用准备好的学具动手折叠验证一下。
(2)是不是所有的平面图形可以围成立体图形?
可以
可以
不可以
不是
(3)图中所示的三棱柱,能不能把它变成一个平面图形?你和周围的同学变成的平面图形一样吗?
2.小组交流,归纳总结.
多面体是由平面图形围成的立体图形,沿着多面体的一些棱把它剪开,可以把多面体的表面展开成一个平面图形。图①和图②叫做三棱锥的表面展开图.三棱柱变成的多种平面图形.
3.继续探究:
①想一想:为什么同一个三棱锥、三棱柱有不同的展开图?其它立体图形的展开图是不是唯一的?
② 小结:同一个立体图形按不同的方式展开,得到的表面展开图不一样。其它立体图形的展开图不是唯一的.
注意:沿着棱剪,展开后是一个图形
可以动手剪,也可以想着画.
4.动手实践,展示交流:
①将一个正方体的表面沿某些棱剪开,能展开成哪些平面图形?
请你根据投影给出的动画剪裁示范,剪裁动手自己准备的正方体.
结束后组内交流,把小组得到的展开图贴在黑板上.
②认真观察,黑板上的展开图有没有重复的?
认真观察分析,把重复的拿下来.
③你认为黑板上的哪几个可以归为一类?为什么归为一类?
④除了黑板上展示的展开图,还有没有其他展开图
5.深入探究,寻找规律
①认真观察老师补充之后的投影上面的11种正方体的展开图有没有什么规律?
蓝
黄
②小组讨论:这些正方体展开图可以分为几类?哪几号展开图可以分为一类,为什么?
③观察立方体相对的两个面在其展开图中的位置有什么特点?
相对的两个面不相连,上下隔一行,左右隔一列
例1请根据表面展开图说出立体图形的名称.
精讲例题
1.精讲例1
分析:表面展开图中,含有三角形时,考虑棱锥或者棱柱;如果只有两个三角形,一定是三棱柱;如果全是长方形,考虑四棱柱,如果全是正方形,一定是正方体;如果含有圆,考虑圆锥或者圆柱.
长方体
四棱锥
圆锥体
圆柱体
三棱柱
正方体
例2如图,若要使图中平面展开图折叠成正方体后,相对的面上的两个数互为相反数,则填入正方形内的三个数x、y、z依次为( )
3.精讲例2
分析:根据正方体表面展开图的特征判断“对面”,再根据相对的面上的两个数互为相反数求出答案即可.
A
A.-2,-3,-1 B.-3,2-1 C.2,-3,-1 D.2,-1,-3
掌握正方体表面展开图的特征、相反数的定义是正确解答的前提
3.精讲例3:
例3如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
解:设展开图的长方形的长为a,宽为b,由图可得:
12=3b,2b+a=22,解得a=14,b=4,
∴长方体的体积为:4×4×14=224,故选:B.
分析:根据展开图,可以求得原来长方体的底面的边长和高,然后根据长方体的体积公式计算即可.
温馨提示:本题考查几何体的展开图的计算应用,解答本题型的关键是明确展示图中对应立体图形的量的大小,利用数形结合的思想解答.
A.144 B.224 C.264 D.300
1、下面的图形那些是立方体的展开图?
课堂练习
长方体
2.如图是正方体的一种展开图,表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”,那么在正方体的表面中与“一”相对的是( )
三棱柱
A
A.一 B.起 C.来 D.!
正方体
四棱锥
3.如图是一个长方体纸盒的展开图,则这个纸盒的体积是 .
(单位:cm3)
24 cm3
4.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是 ;
(2)求该几何体的表面积(结果保留π);
(3)求该几何体的体积(结果保留π).
4解:(1)该几何体的名称是圆柱,
(2)该几何体的表面积为:2π×22+5×4π=28π;
(3)该几何体的体积为:π×22×5=20π.
空间想像能力
动手操作能力
合作探究能力
课堂总结
立体图形
平面图形
立体图形的表面展开图
①有的立体图形是由平面图形围成的
②不是所有平面图形都可以围成为立体图形
③同一个立体图形按不同的方式展开,得到的表面展开图不一样
④正方体的11种表面展开图→相对的面
布置作业
1.是不是所有的平面图形都可以围成立体图形,是不是所有的立体图形都可展开成平面图形?
2.P131-132页1-3题
3.习题4.3的1-3题.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
