初中数学华师大版七上4.6.2角的比较和运算 课件(共18张PPT)
文档属性
| 名称 | 初中数学华师大版七上4.6.2角的比较和运算 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
4.6.2角的比较和运算
初中数学华师大版七上第四章图形的初步认识
温故而知新
2.如何测量角的大小?角的大小与什么有关?与什么无关?角的度量单位是什么?如何进行角的单位换算?
1.前面学习线段的长短比较这一课时,我们主要学习了关于线段的哪些知识?
我们用量角器测量角的大小;
角的大小与角两边张开大小有关,与边的长短无关,
角的度量单位是度、分、秒,
1°=60′;1’=60″
创设情境
以小组为单位,每个人在本上画一个角.
1.观察法:比较明显的一看就知道哪个角大;
2.用量角器量出角的大小;
想一想:如何比较这几个角的大小?
你能想出几种办法?
如果大小相近,不能直观看出来,又没有量角器的情况下该怎么来比较长短呢?
1.阅读教材,获取新知
阅读课本第149页,回答下列问题:
探究新知
(1)比较角的大小的方法:① ;② .
(2)叠合法比较角的大小的基本步骤是什么?.
叠合法
①将两个角的顶点及一边重合
②两个角的另一边落在重合一边的同侧
③观察两个角另一边的位置确定两个角的大小
度量法
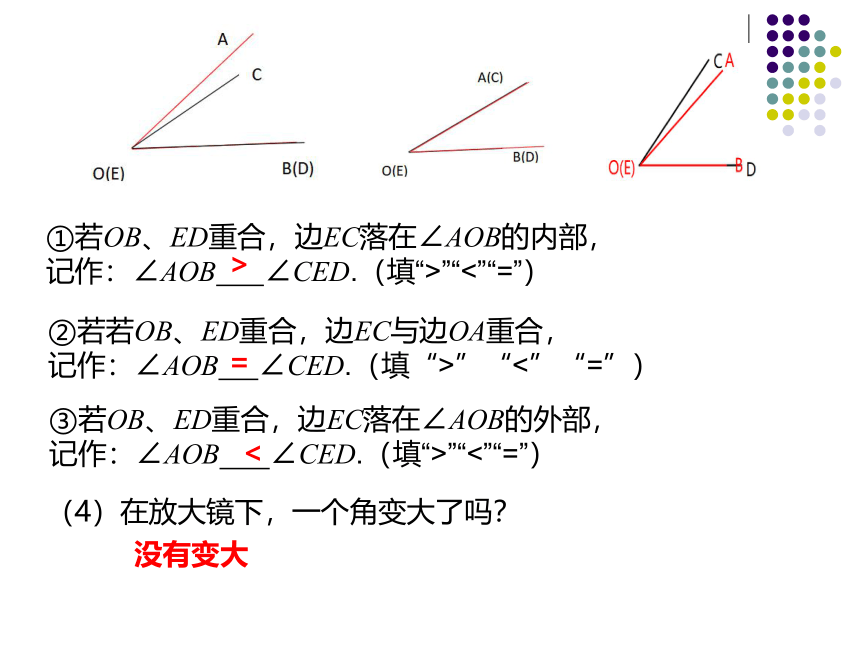
(3)叠合法进行角的大小比较有几种结果?我们怎么用几何语言来表达
③若OB、ED重合,边EC落在∠AOB的外部,
记作:∠AOB ∠CED.(填“>”“<”“=”)
①若OB、ED重合,边EC落在∠AOB的内部,
记作:∠AOB ∠CED.(填“>”“<”“=”)
②若若OB、ED重合,边EC与边OA重合,
记作:∠AOB ∠CED.(填“>”“<”“=”)
>
=
<
(4)在放大镜下,一个角变大了吗?
没有变大
(6)一副三角尺上的角是一些常用的角,可以用它们直接画出 , , , ,同时还可以画出其他一些特殊的角,以小组为单位研究一下,一共可以画出哪些特殊的角?
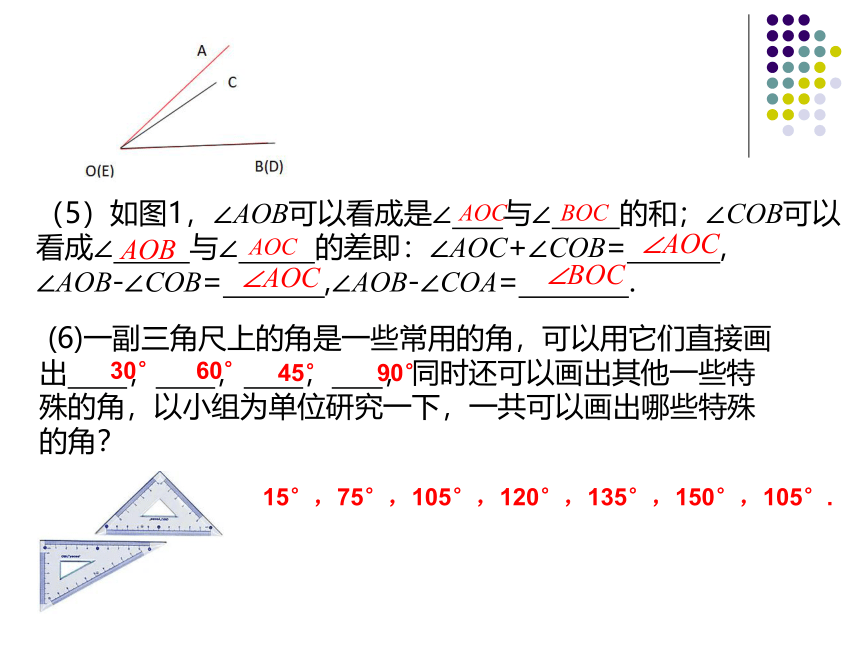
(5)如图1,∠AOB可以看成是∠ 与∠ 的和;∠COB可以看成∠ 与∠ 的差即:∠AOC+∠COB= ,
∠AOB-∠COB= ,∠AOB-∠COA= .
BOC
AOC
∠BOC
∠AOC
∠AOC
AOB
AOC
60°
30°
45°
90°
15°,75°,105°,120°,135°,150°,105°.
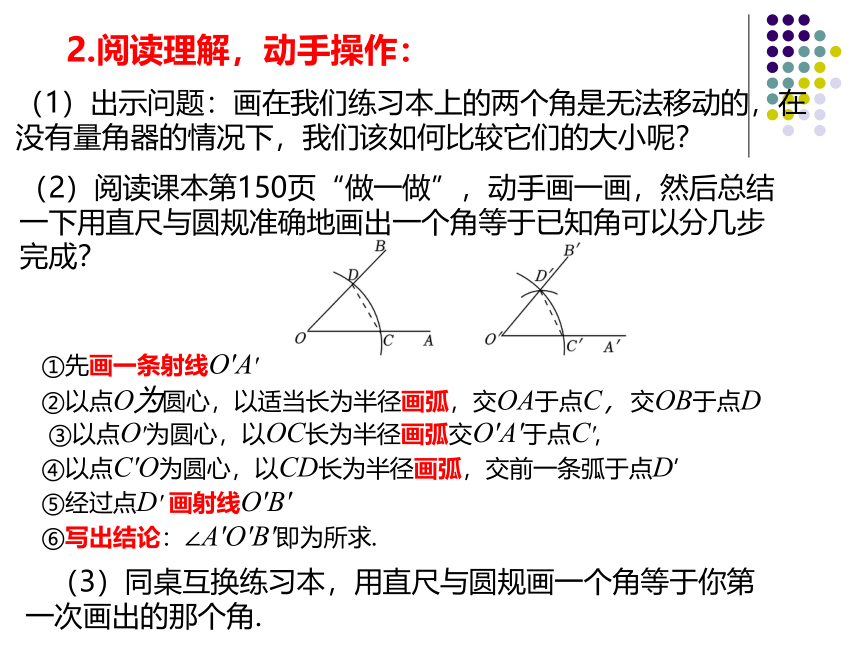
(1)出示问题:画在我们练习本上的两个角是无法移动的,在没有量角器的情况下,我们该如何比较它们的大小呢?
①先画一条射线O′A′
②以点O为圆心,以适当长为半径画弧,交OA于点C,交OB于点D
③以点O′为圆心,以OC长为半径画弧交O′A′于点C′,
④以点C′O为圆心,以CD长为半径画弧,交前一条弧于点D’
⑤经过点D′ 画射线O′B′
⑥写出结论:∠A′O′B′即为所求.
(2)阅读课本第150页“做一做”,动手画一画,然后总结一下用直尺与圆规准确地画出一个角等于已知角可以分几步完成?
2.阅读理解,动手操作:
(3)同桌互换练习本,用直尺与圆规画一个角等于你第一次画出的那个角.
①上一节课我们学过角的单位是度分秒,并且会进行度分秒的换算,我们还要学会简单的加减运算.大家想一想如何计算,计算时需要注意什么?
①相同的计量单位相加,即度加度,分加分,秒加秒
②计算时需要注意满六十进一,不够减时借一当六十.
(1)阅读课本第150页“做一做”下面至151页“练习”上面,回答下列问题:
3.自主阅读,深入探究
计算:18°42′+65°48′ 90°-23°25′
18°42′+65°48′=83°90′=84°30′ 90°-23°25′=89°60′-23°25′=66°35′
②从一个角的顶点引出一条射线,把这个角分成两个相等的角,叫做这个 .
③如图,OC是∠AOB的平分线,∠AOC=30°,则∠COB= .
④如图,OC是∠AOB的平分线,∠AOC=30°,则∠AOB= .
⑤如图,OC是∠AOB的平分线,∠AOB=60°,则∠BOC= .
60°
30°
30°
角的平分线
以小组为单位交流总结:如何做出一个角的平分线?角平分线的几何语言表述有几种?
4.小组合作,总结归纳:
①如图,∵OC是∠AOB的平分线,∴∠BOC= ∠AOB.
②如图,∵OC是∠AOB的平分线,∴∠AOB=2∠AOC.
③如图,∵OC是∠AOB的平分线,∴∠BOC= ∠AOC .
用量角器可以做出
一个角的平分线
例1已知∠α,∠β,求作∠ABC,使得∠ABC=∠α﹣∠β.(不写作法,但要保留作图痕迹)
精讲例题
1.精讲例1
学生试做.
注意:在已知角的内部上画另一条有公共顶点公共边才可以得到差
分析:先作∠ABD=∠α,再在∠ABD内部作∠DBC=∠β,则∠ABC满足条件.
解:如图,∠ABC
即为所求
如图,点O在直线AB上.∠COB=120°请你先画出∠COA的平分线OD,再求出∠BOD的度数.
3.精讲例2
分析:先用量角器画出∠COA的平分线OD,由∠COB=120°和平角AOC可以求出∠BOC的度数,再由OD是∠COB的平分线,可以求出∠ 或∠ 的度数;最后就可以求出∠BOD的度数.
解:∵∠BOC=120°,
∴∠AOC=180°-∠BOC
=180°﹣120°=60°,
∵OD平分∠AOC
∴∠COD= ∠AOC=30°,
∴∠BOD=∠BOC+∠COD
=120°+30°=150°.
COD
AOD
C
A
B
O
想一想:除了你用的方法之外,还可以用什么方法来求∠BOD的度数,试着写出求解过程.
∵∠BOC=120°,
∴∠AOC=180°-∠BOC=180°﹣120°=60°,
∵OD平分∠AOC,
∴∠DOA= ∠AOC=30°,
∴∠BOD=∠BOA-∠AOD=180°-30°=150°.
C
A
B
O
1.如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC D.∠AOC=∠AOB
课堂练习
B
C
2.如图所示,射线OA,OB,OC,OD,点A,O,D在同一直线上.其中点O为量角器半圆的圆心,则从图中可读出∠BOC的度数为( )
A.60° B.70° C.80° D.90°
3.如图,∠AOB=50°,以O为端点画射线OC,使∠BOC=20°,则∠AOC的度数为( )
A.30° B.70° C.50° D.30°或70°
D
4.将一副常规的三角尺如图放置,则图中∠ACB的度数是( )
A.75° B.95° C.15° D.120°
C
5.如图,如果∠1=65°15′,∠2=78°30′,则∠3是多少度?
解:∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2
=180°﹣65°15′﹣78°30′
=36°15′.
故答案为:36°15′.
课堂总结
1.如何比较两个角的大小:
①度量法:从“数值”的角度比较
②叠合法:从“形”的角度比较
2.会用直尺和圆规作一个角等于已知角.
3.知道角的和差仍是角,并会进行度分秒的运算.
4.角的平分线的定义及相关计算
5.类比的学习方法和数形结合的数学思想
布置作业
1.P151页课后练习1-3题;
2.P153页习题4.6的1,5题.
4.6.2角的比较和运算
初中数学华师大版七上第四章图形的初步认识
温故而知新
2.如何测量角的大小?角的大小与什么有关?与什么无关?角的度量单位是什么?如何进行角的单位换算?
1.前面学习线段的长短比较这一课时,我们主要学习了关于线段的哪些知识?
我们用量角器测量角的大小;
角的大小与角两边张开大小有关,与边的长短无关,
角的度量单位是度、分、秒,
1°=60′;1’=60″
创设情境
以小组为单位,每个人在本上画一个角.
1.观察法:比较明显的一看就知道哪个角大;
2.用量角器量出角的大小;
想一想:如何比较这几个角的大小?
你能想出几种办法?
如果大小相近,不能直观看出来,又没有量角器的情况下该怎么来比较长短呢?
1.阅读教材,获取新知
阅读课本第149页,回答下列问题:
探究新知
(1)比较角的大小的方法:① ;② .
(2)叠合法比较角的大小的基本步骤是什么?.
叠合法
①将两个角的顶点及一边重合
②两个角的另一边落在重合一边的同侧
③观察两个角另一边的位置确定两个角的大小
度量法
(3)叠合法进行角的大小比较有几种结果?我们怎么用几何语言来表达
③若OB、ED重合,边EC落在∠AOB的外部,
记作:∠AOB ∠CED.(填“>”“<”“=”)
①若OB、ED重合,边EC落在∠AOB的内部,
记作:∠AOB ∠CED.(填“>”“<”“=”)
②若若OB、ED重合,边EC与边OA重合,
记作:∠AOB ∠CED.(填“>”“<”“=”)
>
=
<
(4)在放大镜下,一个角变大了吗?
没有变大
(6)一副三角尺上的角是一些常用的角,可以用它们直接画出 , , , ,同时还可以画出其他一些特殊的角,以小组为单位研究一下,一共可以画出哪些特殊的角?
(5)如图1,∠AOB可以看成是∠ 与∠ 的和;∠COB可以看成∠ 与∠ 的差即:∠AOC+∠COB= ,
∠AOB-∠COB= ,∠AOB-∠COA= .
BOC
AOC
∠BOC
∠AOC
∠AOC
AOB
AOC
60°
30°
45°
90°
15°,75°,105°,120°,135°,150°,105°.
(1)出示问题:画在我们练习本上的两个角是无法移动的,在没有量角器的情况下,我们该如何比较它们的大小呢?
①先画一条射线O′A′
②以点O为圆心,以适当长为半径画弧,交OA于点C,交OB于点D
③以点O′为圆心,以OC长为半径画弧交O′A′于点C′,
④以点C′O为圆心,以CD长为半径画弧,交前一条弧于点D’
⑤经过点D′ 画射线O′B′
⑥写出结论:∠A′O′B′即为所求.
(2)阅读课本第150页“做一做”,动手画一画,然后总结一下用直尺与圆规准确地画出一个角等于已知角可以分几步完成?
2.阅读理解,动手操作:
(3)同桌互换练习本,用直尺与圆规画一个角等于你第一次画出的那个角.
①上一节课我们学过角的单位是度分秒,并且会进行度分秒的换算,我们还要学会简单的加减运算.大家想一想如何计算,计算时需要注意什么?
①相同的计量单位相加,即度加度,分加分,秒加秒
②计算时需要注意满六十进一,不够减时借一当六十.
(1)阅读课本第150页“做一做”下面至151页“练习”上面,回答下列问题:
3.自主阅读,深入探究
计算:18°42′+65°48′ 90°-23°25′
18°42′+65°48′=83°90′=84°30′ 90°-23°25′=89°60′-23°25′=66°35′
②从一个角的顶点引出一条射线,把这个角分成两个相等的角,叫做这个 .
③如图,OC是∠AOB的平分线,∠AOC=30°,则∠COB= .
④如图,OC是∠AOB的平分线,∠AOC=30°,则∠AOB= .
⑤如图,OC是∠AOB的平分线,∠AOB=60°,则∠BOC= .
60°
30°
30°
角的平分线
以小组为单位交流总结:如何做出一个角的平分线?角平分线的几何语言表述有几种?
4.小组合作,总结归纳:
①如图,∵OC是∠AOB的平分线,∴∠BOC= ∠AOB.
②如图,∵OC是∠AOB的平分线,∴∠AOB=2∠AOC.
③如图,∵OC是∠AOB的平分线,∴∠BOC= ∠AOC .
用量角器可以做出
一个角的平分线
例1已知∠α,∠β,求作∠ABC,使得∠ABC=∠α﹣∠β.(不写作法,但要保留作图痕迹)
精讲例题
1.精讲例1
学生试做.
注意:在已知角的内部上画另一条有公共顶点公共边才可以得到差
分析:先作∠ABD=∠α,再在∠ABD内部作∠DBC=∠β,则∠ABC满足条件.
解:如图,∠ABC
即为所求
如图,点O在直线AB上.∠COB=120°请你先画出∠COA的平分线OD,再求出∠BOD的度数.
3.精讲例2
分析:先用量角器画出∠COA的平分线OD,由∠COB=120°和平角AOC可以求出∠BOC的度数,再由OD是∠COB的平分线,可以求出∠ 或∠ 的度数;最后就可以求出∠BOD的度数.
解:∵∠BOC=120°,
∴∠AOC=180°-∠BOC
=180°﹣120°=60°,
∵OD平分∠AOC
∴∠COD= ∠AOC=30°,
∴∠BOD=∠BOC+∠COD
=120°+30°=150°.
COD
AOD
C
A
B
O
想一想:除了你用的方法之外,还可以用什么方法来求∠BOD的度数,试着写出求解过程.
∵∠BOC=120°,
∴∠AOC=180°-∠BOC=180°﹣120°=60°,
∵OD平分∠AOC,
∴∠DOA= ∠AOC=30°,
∴∠BOD=∠BOA-∠AOD=180°-30°=150°.
C
A
B
O
1.如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC D.∠AOC=∠AOB
课堂练习
B
C
2.如图所示,射线OA,OB,OC,OD,点A,O,D在同一直线上.其中点O为量角器半圆的圆心,则从图中可读出∠BOC的度数为( )
A.60° B.70° C.80° D.90°
3.如图,∠AOB=50°,以O为端点画射线OC,使∠BOC=20°,则∠AOC的度数为( )
A.30° B.70° C.50° D.30°或70°
D
4.将一副常规的三角尺如图放置,则图中∠ACB的度数是( )
A.75° B.95° C.15° D.120°
C
5.如图,如果∠1=65°15′,∠2=78°30′,则∠3是多少度?
解:∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2
=180°﹣65°15′﹣78°30′
=36°15′.
故答案为:36°15′.
课堂总结
1.如何比较两个角的大小:
①度量法:从“数值”的角度比较
②叠合法:从“形”的角度比较
2.会用直尺和圆规作一个角等于已知角.
3.知道角的和差仍是角,并会进行度分秒的运算.
4.角的平分线的定义及相关计算
5.类比的学习方法和数形结合的数学思想
布置作业
1.P151页课后练习1-3题;
2.P153页习题4.6的1,5题.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
