初中数学人教版八上11.3多边形及其内角和 课件 31张PPT
文档属性
| 名称 | 初中数学人教版八上11.3多边形及其内角和 课件 31张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1014.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 21:13:17 | ||
图片预览





文档简介
(共31张PPT)
11.3 多边形及其内角和
1.了解多边形、凹凸多边形、正多边形、多边形的内角、外角、对角线等基本概念.
2.经历探索多边形内角和与外角和公式的过程,体会数学与现实生活的联系.
在实际生活当中,除了三角形,还有许多由线段围成的图形. 观察图片,你能找到由一些线段围成的图形吗?
问题2:观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题1:什么是三角形?
提问
比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
思考
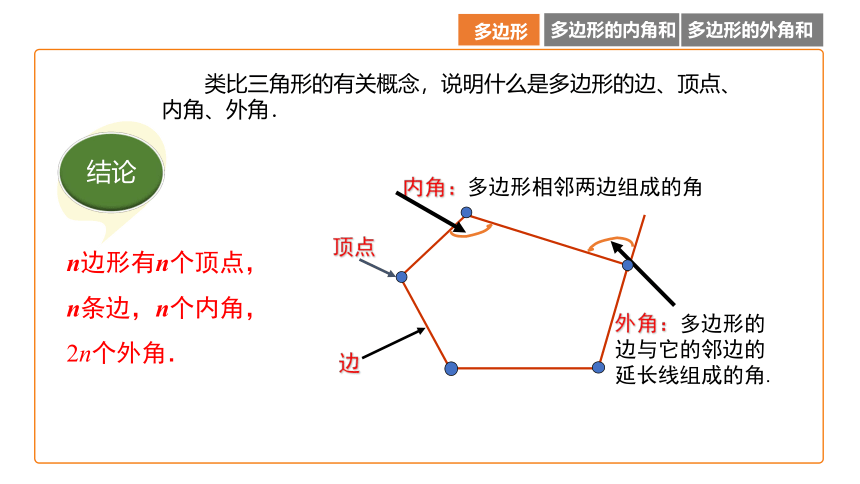
内角:多边形相邻两边组成的角
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
结论
类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
(1)
(2)
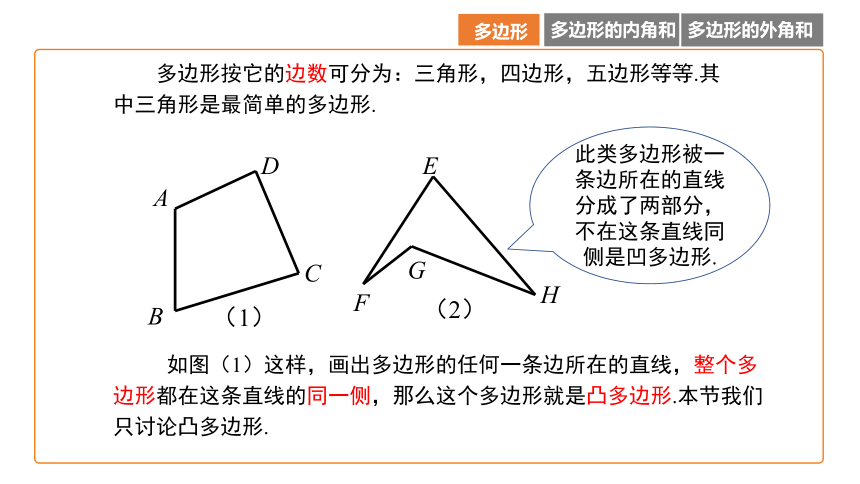
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.本节我们只讨论凸多边形.
A
B
C
D
E
F
G
H
此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
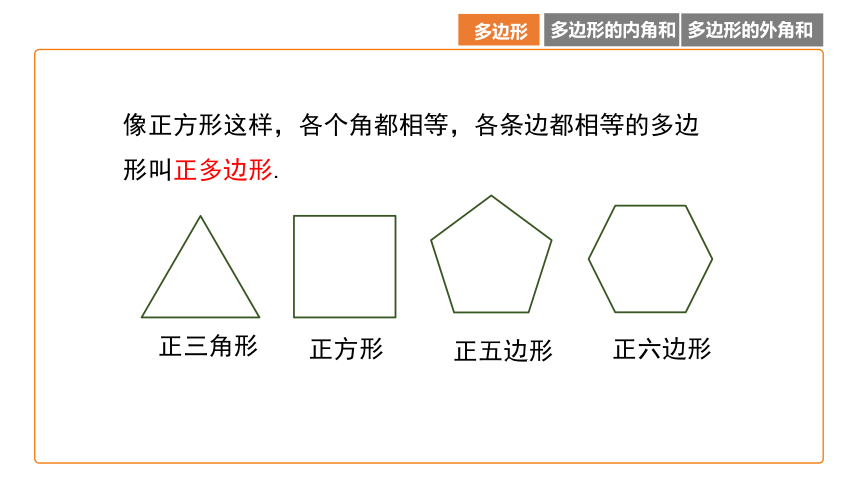
像正方形这样,各个角都相等,各条边都相等的多边形叫正多边形.
正三角形
正方形
正五边形
正六边形
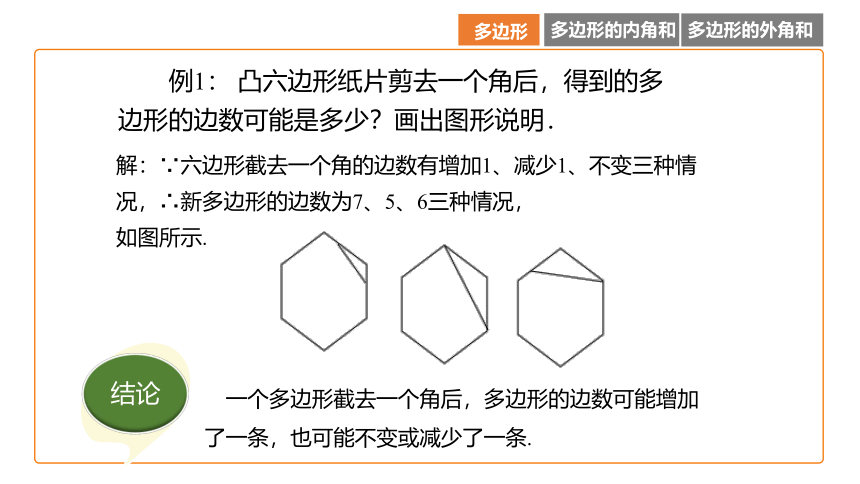
例1: 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,∴新多边形的边数为7、5、6三种情况,
如图所示.
一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.
结论
A
B
C
D
E
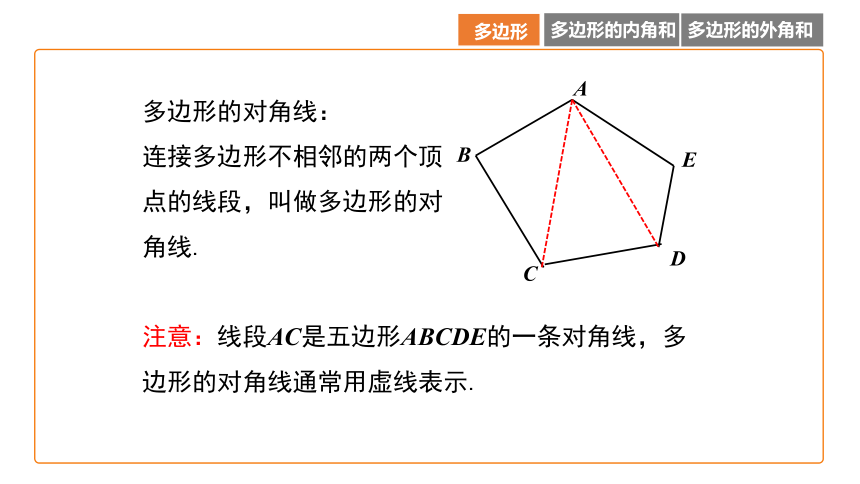
多边形的对角线:
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
注意:线段AC是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.
三角形
六边形
四边形
八边形
……
五边形
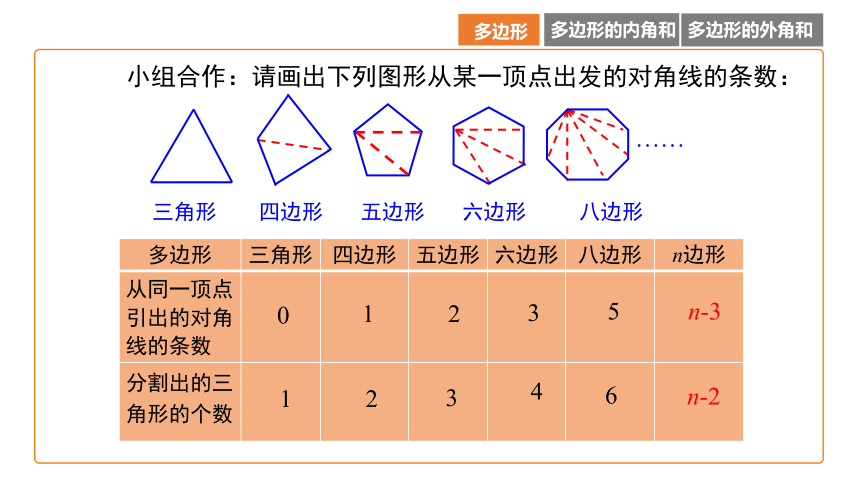
小组合作:请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
结论
若从一个多边形的一个顶点出发,最多可以引10条对角线,则这是 边形.
十三
实践
计算矩形的内角和并利用三角形内角和定理探究任意凸四边形的内角和.
证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=(∠BAC +∠BCA +∠B)
+ (∠DAC +∠DCA +∠D),
= 180° + 180° = 360° .
实践
类比前面的过程,你能探索五边形的内角和吗?六边形呢?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
从n 边形的一个顶点出发,可以作(n -3)条对角线,它们将n 边形分为(n -2)个三角形,这(n -2)个三角形的内角和就是n 边形的内角和,所以,n 边形的内角和等于(n -2)×180°.
通过上述过程,你能说说多边形的内角和与边数的关系吗?
n 边形内角和等于(n -2)×180°.
多边形内角和公式:
例2:如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解: 如图,在四边形ABCD中,∠A+∠C=180°.
∵∠A+∠B+∠C+∠D
=(4-2)×180°=360°
∵∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
A
B
C
D
结论:四边形的一组对角互补,另一组对角也互补.
例3: 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2) 180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为(360°+720°)÷8=135°.
例4:一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
解:设此多边形的内角和为x,
则有1125°<x<1125°+180°,
即180°×6+45°<x<180°×7+45°,
因为x为多边形的内角和,所以它是180°的倍数,
所以x=180°×7=1260°.
所以7+2=9,1260°-1125°=135°.
因此,漏加的这个内角是135°,这个多边形是九边形.
解:由 ∠BAD +∠1 =180°,
∠ABC +∠2 =180°,
∠BCD +∠3 =180°,
∠ADC +∠4 =180°,
得∠BAD + ∠1 + ∠ABC
+∠2 +∠BCD +∠3 +∠ADC +∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,得
∠1 +∠2 +∠3 +∠4 =180°×4 - 180°×2 =360°.
类比三角形的外角和的计算方法求四边形的外角和.
A
B
C
1
2
3
D
4
你能仿照上面的方法求n 边形(n 是不小于3 的任意整数)的外角和吗?
解:因为n 边形的每个内角与它相邻的外角是邻补角,它们的和是180°,所以n 边形内角和加外角和等于n · 180°,所以, n 边形的外角和为:
n · 180°-(n -2)· 180°= 360°.
结论:任意多边形的外角和等于360°.
我们也可以这样理解多边形外角和等于360°.
如图,从多边形的一个顶点A 出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发的方向.
由于走了一周,所转过的各个角的和等于一个周角,所以多边形外角和等于360°.
A
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
探究
例5:已知一个多边形,它的内角和等于外角和的4倍,求这个多边形的边数.
解: 设多边形的边数为n.
(n-2) 180°=4× 360 .
解得 n=10.
∴这个多边形的边数为10.
1.六边形的对角线共有( )
A.6条 B.7条 C.8条 D.9条
2.下列属于正多边形的是( )
A.长方形 B.等边三角形
C.梯形 D.圆
3.若多边形的边数由5增加到7,则其外角和的度数
( )
A.增加 B.减少 C.不变 D.不能确定
D
B
C
4.已知,在四边形ABCD中,∠A:∠B=5:7,∠B与∠A的差等于∠C,∠D与∠C的差是80度,求四边形ABCD四个内角的度数.
解:设∠A=5x°,∠D=y°,则∠B=7x°,∠C=2x°,由题意可得
解得
所以∠A=87.5°,∠B=122.5°,∠C=35°,∠D=115°.
1.多边形的顶点、边、内角、外角、对角线等概念;
2.多边形的分类;
3.多边形的对角线计算方法;
4.多边形的内角和公式;
5.多边形的外角和公式;
6.正多边形的一个外角和一个内角的计算公式.
1.小组合作绘制本节课所有知识点的思维导图.
2.如图,小亮从A点出发,沿直线前进10米,后左转30度,再沿直线前进10米.又向左转30度,…,照这样走下去,他第一次回到出发地A点时,一共走了多少米?
解:由题意可知,小亮第一次回到出发地A点时,他的行走路线是一个正多边形,且这个正多边形的外角等于30°,边长为10米.所以这个多边形的边数为
所以一共走了12×10=120(米).
3.以小组为单位搜集5道考察不同知识点的题目并完成解题.
11.3 多边形及其内角和
1.了解多边形、凹凸多边形、正多边形、多边形的内角、外角、对角线等基本概念.
2.经历探索多边形内角和与外角和公式的过程,体会数学与现实生活的联系.
在实际生活当中,除了三角形,还有许多由线段围成的图形. 观察图片,你能找到由一些线段围成的图形吗?
问题2:观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
问题1:什么是三角形?
提问
比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
思考
内角:多边形相邻两边组成的角
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
结论
类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.本节我们只讨论凸多边形.
A
B
C
D
E
F
G
H
此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
像正方形这样,各个角都相等,各条边都相等的多边形叫正多边形.
正三角形
正方形
正五边形
正六边形
例1: 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,∴新多边形的边数为7、5、6三种情况,
如图所示.
一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.
结论
A
B
C
D
E
多边形的对角线:
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
注意:线段AC是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.
三角形
六边形
四边形
八边形
……
五边形
小组合作:请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
结论
若从一个多边形的一个顶点出发,最多可以引10条对角线,则这是 边形.
十三
实践
计算矩形的内角和并利用三角形内角和定理探究任意凸四边形的内角和.
证明:连接AC,
∠BAD +∠B +∠BCD +∠D
=(∠BAC +∠BCA +∠B)
+ (∠DAC +∠DCA +∠D),
= 180° + 180° = 360° .
实践
类比前面的过程,你能探索五边形的内角和吗?六边形呢?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
从n 边形的一个顶点出发,可以作(n -3)条对角线,它们将n 边形分为(n -2)个三角形,这(n -2)个三角形的内角和就是n 边形的内角和,所以,n 边形的内角和等于(n -2)×180°.
通过上述过程,你能说说多边形的内角和与边数的关系吗?
n 边形内角和等于(n -2)×180°.
多边形内角和公式:
例2:如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解: 如图,在四边形ABCD中,∠A+∠C=180°.
∵∠A+∠B+∠C+∠D
=(4-2)×180°=360°
∵∠B+∠D=360°-(∠A+∠C)
=360°-180°
=180°
A
B
C
D
结论:四边形的一组对角互补,另一组对角也互补.
例3: 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2) 180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
∴它每一个内角的度数为(360°+720°)÷8=135°.
例4:一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
解:设此多边形的内角和为x,
则有1125°<x<1125°+180°,
即180°×6+45°<x<180°×7+45°,
因为x为多边形的内角和,所以它是180°的倍数,
所以x=180°×7=1260°.
所以7+2=9,1260°-1125°=135°.
因此,漏加的这个内角是135°,这个多边形是九边形.
解:由 ∠BAD +∠1 =180°,
∠ABC +∠2 =180°,
∠BCD +∠3 =180°,
∠ADC +∠4 =180°,
得∠BAD + ∠1 + ∠ABC
+∠2 +∠BCD +∠3 +∠ADC +∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,得
∠1 +∠2 +∠3 +∠4 =180°×4 - 180°×2 =360°.
类比三角形的外角和的计算方法求四边形的外角和.
A
B
C
1
2
3
D
4
你能仿照上面的方法求n 边形(n 是不小于3 的任意整数)的外角和吗?
解:因为n 边形的每个内角与它相邻的外角是邻补角,它们的和是180°,所以n 边形内角和加外角和等于n · 180°,所以, n 边形的外角和为:
n · 180°-(n -2)· 180°= 360°.
结论:任意多边形的外角和等于360°.
我们也可以这样理解多边形外角和等于360°.
如图,从多边形的一个顶点A 出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发的方向.
由于走了一周,所转过的各个角的和等于一个周角,所以多边形外角和等于360°.
A
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
探究
例5:已知一个多边形,它的内角和等于外角和的4倍,求这个多边形的边数.
解: 设多边形的边数为n.
(n-2) 180°=4× 360 .
解得 n=10.
∴这个多边形的边数为10.
1.六边形的对角线共有( )
A.6条 B.7条 C.8条 D.9条
2.下列属于正多边形的是( )
A.长方形 B.等边三角形
C.梯形 D.圆
3.若多边形的边数由5增加到7,则其外角和的度数
( )
A.增加 B.减少 C.不变 D.不能确定
D
B
C
4.已知,在四边形ABCD中,∠A:∠B=5:7,∠B与∠A的差等于∠C,∠D与∠C的差是80度,求四边形ABCD四个内角的度数.
解:设∠A=5x°,∠D=y°,则∠B=7x°,∠C=2x°,由题意可得
解得
所以∠A=87.5°,∠B=122.5°,∠C=35°,∠D=115°.
1.多边形的顶点、边、内角、外角、对角线等概念;
2.多边形的分类;
3.多边形的对角线计算方法;
4.多边形的内角和公式;
5.多边形的外角和公式;
6.正多边形的一个外角和一个内角的计算公式.
1.小组合作绘制本节课所有知识点的思维导图.
2.如图,小亮从A点出发,沿直线前进10米,后左转30度,再沿直线前进10米.又向左转30度,…,照这样走下去,他第一次回到出发地A点时,一共走了多少米?
解:由题意可知,小亮第一次回到出发地A点时,他的行走路线是一个正多边形,且这个正多边形的外角等于30°,边长为10米.所以这个多边形的边数为
所以一共走了12×10=120(米).
3.以小组为单位搜集5道考察不同知识点的题目并完成解题.
