初中数学人教版八上14.1.3积的乘方 课件(共23张PPT)
文档属性
| 名称 | 初中数学人教版八上14.1.3积的乘方 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 430.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
14.1.3 积的乘方
1. 通过探索积的乘方的运算性质,进一步体会和巩固幂的意义,在推理得出积的乘方的运算性质的过程中,领会这个性质.
2.经历探索积的乘方的过程,发展学生的推理能力和有条理的表达能力,培养学生的综合能力.
3.通过小组合作与交流,培养学生团结协作的精神和探索精神,有助于塑造他们挑战困难,挑战生活的勇气和信心.
(am)n=______ (m,n都是正整数).
1.同底数幂乘法法则
2.幂的乘方法则
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘.
a m ·a n =________( m、n都为正整数).
a m+n
amn
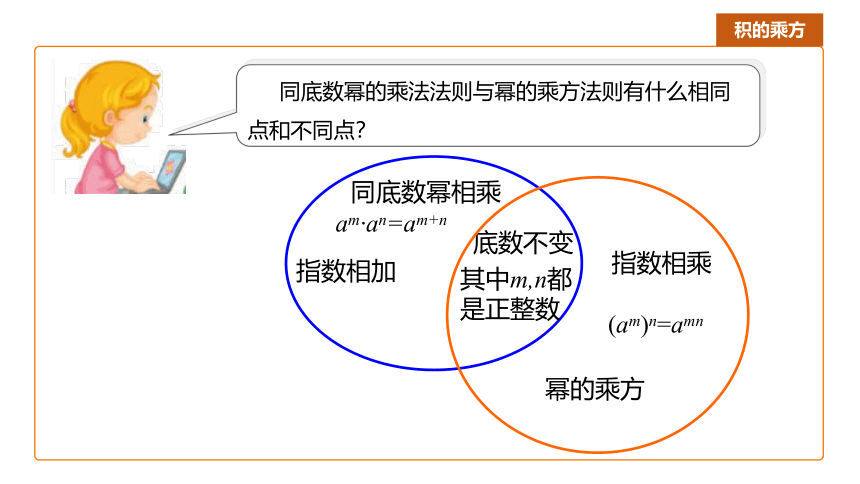
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
(am)n=amn
am·an=am+n
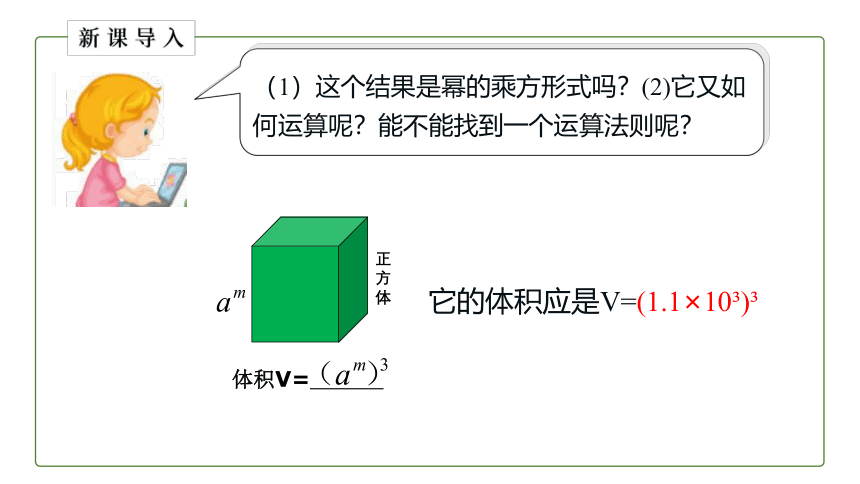
这个正方体的棱长为1.1×10 时,你能计算出它的体积是多少吗 ?
体积V=
正方体
它的体积应是V=(1.1×10 )
(1)这个结果是幂的乘方形式吗?(2)它又如何运算呢?能不能找到一个运算法则呢?
2.比较下列各组算式的计算结果:
[2 ×(-3)]2 与 22 ×(-3)2
[(-2)×(-5)]3与(-2)3 ×(-5)3
1.计算: (2×3)2与22 × 32,我们发现了什么?
∵ (2×3)2=62=36,
22 ×32=4×9=36,
∴ (2×3)2 =22 × 32.
看看运算过程中用到哪些运算律,从运算结果看能发现什么规律?
(1)(ab)2=(ab)·(ab)=(a·a)·(b·b)
=a( )b( )
(2)(ab)3=_______________
=___________
=a( )b( )
2
2
(ab)·(ab)·(ab)
(aaa)·(bbb)
3
3
n个a
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
n个b
=anbn
即:(ab)n=anbn (n为正整数)
=(a·a· ··· ·a)·(b·b· ··· ·b)
思考:积的乘方法则?
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
积的乘方法则
推广:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
结论
积的乘方法则的逆用:
anbn=(ab)n(n为正整数)
例1:计算:
(1)(2a)3; (2)(-5b)3 ;
(3)(xy2)2; (4)(-2x3)4.
解:(1)(2a)3=23 a3 = 8a3;
(2)(-5b)3=(-5)3 b3=-125b3;
(3)(xy2)2=x2 (y2)2=x2y4;
(4)(-2x3)4=(-2)4 (x3)4=16x12.
1.计算:
(1)(ab2)3
(2)(3a2b3)3
(3)-(-x3y2)2
=a3 (b2)3
=a3b6
= 33 (a2)3 (b3)3
= 27a6b9
= -(-)2 (x3)2 (y2)2
=-x6y4
2.(1)(ab)4 ; (2) (-2xy)3;
(3)(-3×102)3 ; (4) (2ab2)3.
3.(1) ; (2) -(-3a2b3)4;
(3)(-x3y2)5 ; (4) ;
a4b4
–8x3y3
–2.7×107
8a3b6
-81a8b12
-x15y10
a11
4. (1) [-4(x-y)2]3; (2) [3(a+b)(a-c)]4;
-64(x-y)6
81(a+b)4 (a-c)4
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7.
(2)(3xy2)2+(-4xy3) · (-xy) .
(3)(-2x3)3·(x2)2.
【解析】原式=2x6·x3-27x9+25x2·x7= 2x9-27x9+25x9 = 0.
【解析】原式=9x2y4 +4x2y4=13x2y4.
【解析】原式= -8x9·x4 =-8x13.
注意:运算顺序是
先乘方,再乘除,
最后算加减.
例2:计算.
1.计算(-4×103)2×(-2×103)3的结果是( )
A.1.08×1017 B.-1.28×1017
C.4.8×1016 D.-2.4×1016
B
2.计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7
解:原式=2x6 · x3-27x9+25x2 ·x7
注意:运算顺序是先乘方,再乘除, 最后算加减.
=2x9-27x9+25x9
=0
(ab)n = an·bn
逆运算:
an·bn = (ab)n
试用简便方法计算:
(1) 23×53
(2)(-5)15 × (-2)15
= (2×5)3
= 103
= [(-5)×(-2)]15
= 1015
(0.04)2004×[(-5)2004]2=
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
=14008
解法一: (0.04)2004×[(-5)2004]2
=1
=(0.04)2004 × [(-5)2]2004
解法二: (0.04)2004×[(-5)2004]2
=(0.04×25)2004
=12004
=1
= (0.04)2004 ×(25)2004
说明:逆用积的乘方法则 可以化简一些复杂的计算.
48×0.258=
(0.04)2004×[(-5)2004]2=
(40.25)8=1
(-)2013=-1
(0.04)2004×[(-5)2]2004 = (0.04×25)2004 =1
(0.125)16× (-8)16 × (-8) = -8
即学即练:
D
A
3.计算: (1)(-2x2y3)3 (2) (-3a3b2c)4
解:(1)原式=(-2)3 ·(x2)3 ·(y3)3=-8x6y9;
(2)原式=(-3)4 ·(a3)4 ·(b2)4 · c4
= 81 a12b8c4.
4.如果(an bm b)3=a9b15 ,求m , n的值.
(an)3 (bm)3 b3=a9b15 ,
a 3n b 3m b3=a9b15,
a 3n b 3m+3=a9b15 ,
3n=9, 3m+3=15,
n=3,m=4.
解: (an bm b)3=a9b15 ,
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
反向运用
am+n = am · an
amn = (am)n
an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序).
1.(1)已知n为正整数,且x3n=2,求(2x3n)2+(-3x2n)3的值;
【解析】原式=4(x3n)2-27(x3n)2=-23(x3n)2=-92.
(2)已知2x+3·3x+3=36x-2,求x的值.
【解析】7.
(3)当a3b2=72时,求a6b4的值.
【解析】a6b4=(a3b2)2=722=5 184.
2.完成本节课配套习题.
14.1.3 积的乘方
1. 通过探索积的乘方的运算性质,进一步体会和巩固幂的意义,在推理得出积的乘方的运算性质的过程中,领会这个性质.
2.经历探索积的乘方的过程,发展学生的推理能力和有条理的表达能力,培养学生的综合能力.
3.通过小组合作与交流,培养学生团结协作的精神和探索精神,有助于塑造他们挑战困难,挑战生活的勇气和信心.
(am)n=______ (m,n都是正整数).
1.同底数幂乘法法则
2.幂的乘方法则
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘.
a m ·a n =________( m、n都为正整数).
a m+n
amn
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
(am)n=amn
am·an=am+n
这个正方体的棱长为1.1×10 时,你能计算出它的体积是多少吗 ?
体积V=
正方体
它的体积应是V=(1.1×10 )
(1)这个结果是幂的乘方形式吗?(2)它又如何运算呢?能不能找到一个运算法则呢?
2.比较下列各组算式的计算结果:
[2 ×(-3)]2 与 22 ×(-3)2
[(-2)×(-5)]3与(-2)3 ×(-5)3
1.计算: (2×3)2与22 × 32,我们发现了什么?
∵ (2×3)2=62=36,
22 ×32=4×9=36,
∴ (2×3)2 =22 × 32.
看看运算过程中用到哪些运算律,从运算结果看能发现什么规律?
(1)(ab)2=(ab)·(ab)=(a·a)·(b·b)
=a( )b( )
(2)(ab)3=_______________
=___________
=a( )b( )
2
2
(ab)·(ab)·(ab)
(aaa)·(bbb)
3
3
n个a
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
n个b
=anbn
即:(ab)n=anbn (n为正整数)
=(a·a· ··· ·a)·(b·b· ··· ·b)
思考:积的乘方法则?
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
积的乘方法则
推广:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
结论
积的乘方法则的逆用:
anbn=(ab)n(n为正整数)
例1:计算:
(1)(2a)3; (2)(-5b)3 ;
(3)(xy2)2; (4)(-2x3)4.
解:(1)(2a)3=23 a3 = 8a3;
(2)(-5b)3=(-5)3 b3=-125b3;
(3)(xy2)2=x2 (y2)2=x2y4;
(4)(-2x3)4=(-2)4 (x3)4=16x12.
1.计算:
(1)(ab2)3
(2)(3a2b3)3
(3)-(-x3y2)2
=a3 (b2)3
=a3b6
= 33 (a2)3 (b3)3
= 27a6b9
= -(-)2 (x3)2 (y2)2
=-x6y4
2.(1)(ab)4 ; (2) (-2xy)3;
(3)(-3×102)3 ; (4) (2ab2)3.
3.(1) ; (2) -(-3a2b3)4;
(3)(-x3y2)5 ; (4) ;
a4b4
–8x3y3
–2.7×107
8a3b6
-81a8b12
-x15y10
a11
4. (1) [-4(x-y)2]3; (2) [3(a+b)(a-c)]4;
-64(x-y)6
81(a+b)4 (a-c)4
(1) 2(x3)2·x3-(3x3)3+(5x)2·x7.
(2)(3xy2)2+(-4xy3) · (-xy) .
(3)(-2x3)3·(x2)2.
【解析】原式=2x6·x3-27x9+25x2·x7= 2x9-27x9+25x9 = 0.
【解析】原式=9x2y4 +4x2y4=13x2y4.
【解析】原式= -8x9·x4 =-8x13.
注意:运算顺序是
先乘方,再乘除,
最后算加减.
例2:计算.
1.计算(-4×103)2×(-2×103)3的结果是( )
A.1.08×1017 B.-1.28×1017
C.4.8×1016 D.-2.4×1016
B
2.计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7
解:原式=2x6 · x3-27x9+25x2 ·x7
注意:运算顺序是先乘方,再乘除, 最后算加减.
=2x9-27x9+25x9
=0
(ab)n = an·bn
逆运算:
an·bn = (ab)n
试用简便方法计算:
(1) 23×53
(2)(-5)15 × (-2)15
= (2×5)3
= 103
= [(-5)×(-2)]15
= 1015
(0.04)2004×[(-5)2004]2=
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
=14008
解法一: (0.04)2004×[(-5)2004]2
=1
=(0.04)2004 × [(-5)2]2004
解法二: (0.04)2004×[(-5)2004]2
=(0.04×25)2004
=12004
=1
= (0.04)2004 ×(25)2004
说明:逆用积的乘方法则 可以化简一些复杂的计算.
48×0.258=
(0.04)2004×[(-5)2004]2=
(40.25)8=1
(-)2013=-1
(0.04)2004×[(-5)2]2004 = (0.04×25)2004 =1
(0.125)16× (-8)16 × (-8) = -8
即学即练:
D
A
3.计算: (1)(-2x2y3)3 (2) (-3a3b2c)4
解:(1)原式=(-2)3 ·(x2)3 ·(y3)3=-8x6y9;
(2)原式=(-3)4 ·(a3)4 ·(b2)4 · c4
= 81 a12b8c4.
4.如果(an bm b)3=a9b15 ,求m , n的值.
(an)3 (bm)3 b3=a9b15 ,
a 3n b 3m b3=a9b15,
a 3n b 3m+3=a9b15 ,
3n=9, 3m+3=15,
n=3,m=4.
解: (an bm b)3=a9b15 ,
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
反向运用
am+n = am · an
amn = (am)n
an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序).
1.(1)已知n为正整数,且x3n=2,求(2x3n)2+(-3x2n)3的值;
【解析】原式=4(x3n)2-27(x3n)2=-23(x3n)2=-92.
(2)已知2x+3·3x+3=36x-2,求x的值.
【解析】7.
(3)当a3b2=72时,求a6b4的值.
【解析】a6b4=(a3b2)2=722=5 184.
2.完成本节课配套习题.
