初中数学人教版八上14.1.4整式的乘法 第1课时 课件(共29张PPT)
文档属性
| 名称 | 初中数学人教版八上14.1.4整式的乘法 第1课时 课件(共29张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 418.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
pa+pb+pc
p
p
a
pa
pc
pb
b
14.1.4 整式乘法1
1.理解单项式乘法和单项式与多项式相乘的法则,会用乘法法则进行运算;
2.经历乘法法则的形成过程,发展学生的运算能力,体会类比思想.
3.学生从已有知识出发,通过适当的探究,获得一些直接的经验,体会数学的实用价值.
怎样计算(3×105)×(5×102) 计算过程中用到了哪些运算律及运算性质
(3×105)×(5×102)
=(3×5)×(105×102)
=15×107
乘法交换律、结合律
同底数幂的乘法
=1.5×108.
5a4
如果将式中的数字改为字母,怎样计算这个式子?
5___
·
1.2___
a4
a3
=(___×____)(___·____)=____
5
a4
a3
6a7
·
(-1.2a3b2)
=[__×(-1.2)] ●(a4a3 )
5
b2
=-6a7b2
1.2
你能发现运算规律吗
1.系数相乘
2.同底数的幂相乘
3.只在一个单项式里含有的字母,连同它的指数作为积的一个因式.
用前面发现的方法来试一试!
ac5·2bc2=2(a·b)·(c5·c2)
(乘法交换律、结合律)
(同底数幂的乘法)
=2abc5+2
=2abc7.
结论
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
注意
例1:计算:
(1)(-5a2b)(-3a); (2)(2x)3(-5xy2).
(2) 原式=8x3·(-5xy2)
=[8×(-5)](x3·x)·y2
=-40x4y2
解:(1) 原式=[(-5)×(-3)](a2·a)·b =15a3b
(1)先做乘方,再做单项式相乘;
(2)系数相乘不要漏掉负号.
比较以上两题你发现了哪些注意事项?
口算:
(1)5x2y2.(-3x2y)
(2) (x2)2 .(-2x3y2)2
(3)(1.2×103) ·(5×102)
原式=5×(-3)(x2x2)(y2y)
原式=x4.4x6y4
=4x10y4
=-15x4y3
原式=(1.2×5)×103×102
=6×105
×
×
×
×
判断正误:
(1)4a2 2a4 = 8a8 ( )
(2)6a3 5a2=11a5 ( )
(3)(-7a) (-3a3) =-21a4 ( )
(4)3a2b 4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
求单项式 , , 的积.
这里有三个单项式相乘,还可以利用上面的法则吗?
解:
变式:已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
解:∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴m2+n=7.
解得
总结:单项式乘以单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.
1.当m为偶数时,(a-b)m·(b-a)n与(b-a)m+n的关系是( )
A.相等 B.互为相反数 C.不相等 D.不确定
2.若(8×106)×(5×102)×(2×10)=m×10n (1≤m<10),则m,n的值分别为( )
A.m=8,n=8 B.m=2,n=9 C.m=8,n=10 D.m=5,n=10
3.若(am · bn)·(a2 ·b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5
A
C
D
4.计算:
3x3y·(-2y)2-(-xy)2·(-xy)-xy3·(-4x)2.
解:原式=3xy3·4y2-x2y2· (-xy)-xy3·16x2
=12x3y3+x3y3-16x3y3
=-3x3y3
5.如图,王大伯有一块长方形菜地,
他把这块菜地分为6个大小相等
的菜畦,每个菜畦的宽都是a米,
长都是ka米,这块菜地的面积是多少?
a
a
ka
ka
ka
S=
解:
2a·3ka
=(2×3)
ka·a
=6ka2(平方米)
答:这块菜地的面积是6ka2 平方米.
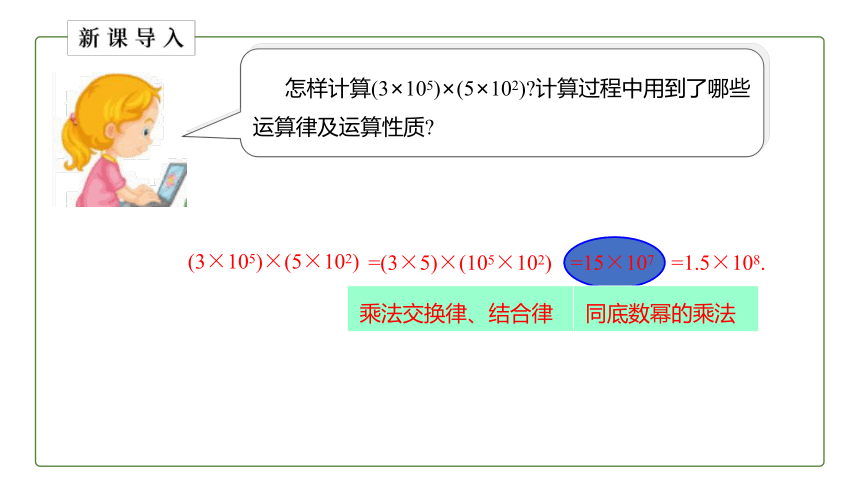
为了扩大绿地的面积,要把街心花园的一块长p 米,宽b 米的长方形绿地,向两边分别加宽a 米和c 米,你能用几种方法表示扩大后的绿地的面积?
方法一:看作一个长方形,计算它的面积.
面积:(a+b+c)p
方法二:看作3个长方形,计算它们的面积和.
面积:pa+pb+pc
pa+pb+pc
p(a+b+c)
你能用自己的语言概括出单项式乘多项式的法则吗?
(a+b+c)p=pa+pb+pc
即单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
结论
(1)依据是乘法分配律;(2)积的项数与多项式的项数相同.
注意
例2:计算:
(1)(-4x)·(2x2+3x-1);
解:(1)(-4x)·(2x2+3x-1)
=
=-8x3-12x2+4x;
(-4x)·(2x2)
(-4x)·3x
(-4x)·(-1)
+
(2)原式
+
1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同;
2.在单项式乘法运算中要注意系数的符号;
3.不要出现漏乘现象,运算要有顺序.
注意
①
②
③
×
×
×
判断正误:
-2a2·(ab+b2)-5a(a2b-ab2)
解:原式=-2a3b-2a2b2-5a3b+5a2b2
=-2a3b-2a2b2-5a3b+5a2b2
注意:单项式与多项式相乘的结果中有同类项,应将同类项合并.
=-7a3b+3a2b2
例3:
变式:先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
当a=-2时,
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
原式=-20×4-9×2=-98.
1.若(ambn)·(a2b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5
2.填空
(1)4(a-b+1)=___________;
(2)3x(2x-y2)=__________;
(3)(2x-5y+6z)(-3x)=_______________;
(4)(-2a2)2(-a-2b+c)=_______________.
D
4a-4b+4
6x2-3xy2
-6x2+15xy-18xz
-4a5-8a4b+4a4c
3.解方程:8x(5-x)=34-2x(4x-3).
解得:x=1.
解:40x-8x2=34-8x2+6x,
40x-6x=34,
34x=34,
4.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=(-2x2)·xy+(-2x2)·y2+(-5x)·x2y+(-5x)·(-xy2)
=-2x3y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3y+3x2y2.
5.解方程:8x(5-x)=34-2x(4x-3).
解得:x=1.
解:40x-8x2=34-8x2+6x,
40x-6x=34,
34x=34,
整式乘法
单项式×单项式
实质上是转化为同底数幂的运算
单项式×
多项式
实质上是转化为单项式×单项式
四点注意
(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负;
(2)不要出现漏乘现象;
(3)运算要有顺序:先乘方,再乘除,最后加减;
(4)对于混合运算,注意最后应合并同类项.
1.细心填一填.
(1)(-2a2·b3)(-3a·b)= ;
(2)(4×105)·(5×104)= ;
(3)(-2ab2)2(-a2·b)= .
6a3b4
2×1010
-4a4b5
2.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-2x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则
∴A=4x2-2x+1.
∴A·(-3x2)=(4x2-2x+1)(-3x2)
A+(-3x2)=x2-2x+1,
=-12x4+6x3-3x2.
3.完成本节课配套习题.
pa+pb+pc
p
p
a
pa
pc
pb
b
14.1.4 整式乘法1
1.理解单项式乘法和单项式与多项式相乘的法则,会用乘法法则进行运算;
2.经历乘法法则的形成过程,发展学生的运算能力,体会类比思想.
3.学生从已有知识出发,通过适当的探究,获得一些直接的经验,体会数学的实用价值.
怎样计算(3×105)×(5×102) 计算过程中用到了哪些运算律及运算性质
(3×105)×(5×102)
=(3×5)×(105×102)
=15×107
乘法交换律、结合律
同底数幂的乘法
=1.5×108.
5a4
如果将式中的数字改为字母,怎样计算这个式子?
5___
·
1.2___
a4
a3
=(___×____)(___·____)=____
5
a4
a3
6a7
·
(-1.2a3b2)
=[__×(-1.2)] ●(a4a3 )
5
b2
=-6a7b2
1.2
你能发现运算规律吗
1.系数相乘
2.同底数的幂相乘
3.只在一个单项式里含有的字母,连同它的指数作为积的一个因式.
用前面发现的方法来试一试!
ac5·2bc2=2(a·b)·(c5·c2)
(乘法交换律、结合律)
(同底数幂的乘法)
=2abc5+2
=2abc7.
结论
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
注意
例1:计算:
(1)(-5a2b)(-3a); (2)(2x)3(-5xy2).
(2) 原式=8x3·(-5xy2)
=[8×(-5)](x3·x)·y2
=-40x4y2
解:(1) 原式=[(-5)×(-3)](a2·a)·b =15a3b
(1)先做乘方,再做单项式相乘;
(2)系数相乘不要漏掉负号.
比较以上两题你发现了哪些注意事项?
口算:
(1)5x2y2.(-3x2y)
(2) (x2)2 .(-2x3y2)2
(3)(1.2×103) ·(5×102)
原式=5×(-3)(x2x2)(y2y)
原式=x4.4x6y4
=4x10y4
=-15x4y3
原式=(1.2×5)×103×102
=6×105
×
×
×
×
判断正误:
(1)4a2 2a4 = 8a8 ( )
(2)6a3 5a2=11a5 ( )
(3)(-7a) (-3a3) =-21a4 ( )
(4)3a2b 4a3=12a5 ( )
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
求系数的积,应注意符号
求单项式 , , 的积.
这里有三个单项式相乘,还可以利用上面的法则吗?
解:
变式:已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
解:∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴m2+n=7.
解得
总结:单项式乘以单项式就是把它们的系数和同底数幂分别相乘,结合同类项的定义,列出二元一次方程组求出参数的值,然后代入求值即可.
1.当m为偶数时,(a-b)m·(b-a)n与(b-a)m+n的关系是( )
A.相等 B.互为相反数 C.不相等 D.不确定
2.若(8×106)×(5×102)×(2×10)=m×10n (1≤m<10),则m,n的值分别为( )
A.m=8,n=8 B.m=2,n=9 C.m=8,n=10 D.m=5,n=10
3.若(am · bn)·(a2 ·b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5
A
C
D
4.计算:
3x3y·(-2y)2-(-xy)2·(-xy)-xy3·(-4x)2.
解:原式=3xy3·4y2-x2y2· (-xy)-xy3·16x2
=12x3y3+x3y3-16x3y3
=-3x3y3
5.如图,王大伯有一块长方形菜地,
他把这块菜地分为6个大小相等
的菜畦,每个菜畦的宽都是a米,
长都是ka米,这块菜地的面积是多少?
a
a
ka
ka
ka
S=
解:
2a·3ka
=(2×3)
ka·a
=6ka2(平方米)
答:这块菜地的面积是6ka2 平方米.
为了扩大绿地的面积,要把街心花园的一块长p 米,宽b 米的长方形绿地,向两边分别加宽a 米和c 米,你能用几种方法表示扩大后的绿地的面积?
方法一:看作一个长方形,计算它的面积.
面积:(a+b+c)p
方法二:看作3个长方形,计算它们的面积和.
面积:pa+pb+pc
pa+pb+pc
p(a+b+c)
你能用自己的语言概括出单项式乘多项式的法则吗?
(a+b+c)p=pa+pb+pc
即单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
结论
(1)依据是乘法分配律;(2)积的项数与多项式的项数相同.
注意
例2:计算:
(1)(-4x)·(2x2+3x-1);
解:(1)(-4x)·(2x2+3x-1)
=
=-8x3-12x2+4x;
(-4x)·(2x2)
(-4x)·3x
(-4x)·(-1)
+
(2)原式
+
1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同;
2.在单项式乘法运算中要注意系数的符号;
3.不要出现漏乘现象,运算要有顺序.
注意
①
②
③
×
×
×
判断正误:
-2a2·(ab+b2)-5a(a2b-ab2)
解:原式=-2a3b-2a2b2-5a3b+5a2b2
=-2a3b-2a2b2-5a3b+5a2b2
注意:单项式与多项式相乘的结果中有同类项,应将同类项合并.
=-7a3b+3a2b2
例3:
变式:先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
当a=-2时,
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
原式=-20×4-9×2=-98.
1.若(ambn)·(a2b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5
2.填空
(1)4(a-b+1)=___________;
(2)3x(2x-y2)=__________;
(3)(2x-5y+6z)(-3x)=_______________;
(4)(-2a2)2(-a-2b+c)=_______________.
D
4a-4b+4
6x2-3xy2
-6x2+15xy-18xz
-4a5-8a4b+4a4c
3.解方程:8x(5-x)=34-2x(4x-3).
解得:x=1.
解:40x-8x2=34-8x2+6x,
40x-6x=34,
34x=34,
4.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=(-2x2)·xy+(-2x2)·y2+(-5x)·x2y+(-5x)·(-xy2)
=-2x3y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3y+3x2y2.
5.解方程:8x(5-x)=34-2x(4x-3).
解得:x=1.
解:40x-8x2=34-8x2+6x,
40x-6x=34,
34x=34,
整式乘法
单项式×单项式
实质上是转化为同底数幂的运算
单项式×
多项式
实质上是转化为单项式×单项式
四点注意
(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负;
(2)不要出现漏乘现象;
(3)运算要有顺序:先乘方,再乘除,最后加减;
(4)对于混合运算,注意最后应合并同类项.
1.细心填一填.
(1)(-2a2·b3)(-3a·b)= ;
(2)(4×105)·(5×104)= ;
(3)(-2ab2)2(-a2·b)= .
6a3b4
2×1010
-4a4b5
2.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-2x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则
∴A=4x2-2x+1.
∴A·(-3x2)=(4x2-2x+1)(-3x2)
A+(-3x2)=x2-2x+1,
=-12x4+6x3-3x2.
3.完成本节课配套习题.
