初中数学人教版九下27.2.1相似三角形的判定 (第2课时) 课件(共22张PPT)
文档属性
| 名称 | 初中数学人教版九下27.2.1相似三角形的判定 (第2课时) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 658.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第二十七章 相似
27.2.1 相似三角形的判定 第2课时
学习目标
掌握“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理,并能解决简单问题.(重点)
判定定理“三边成比例的两个三角形相似”的证明.(难点)
新课导入
活动一、复习“旧知”,关联“新知”
1.现在我们已经学过哪些判定两个三角形相似的方法?
(1). 定义法:若△ABC与△A′B′C′ 满足:
△ABC∽△A' B ' C '
(2).平行推相似:
DE∥BC
△ABC∽△ADE
新课导入
活动一、复习“旧知”,关联“新知”
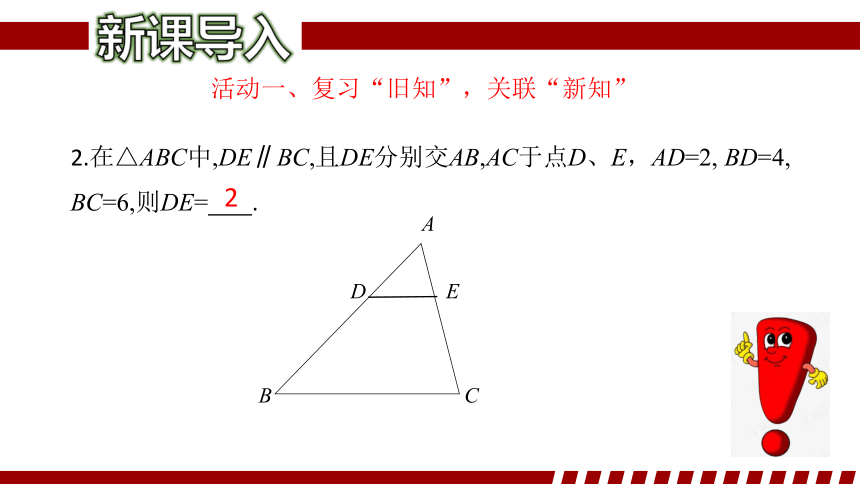
2.在△ABC中,DE∥BC,且DE分别交AB,AC于点D、E,AD=2, BD=4,
BC=6,则DE= .
A
D
E
C
B
2
新课导入
活动二、抓住“本质”,类比猜想
1.一般三角形全等的判定方法有什么?
2.全等是相似比为1的特殊情形,类比判定两个三角形
全等的方法,是否有判定两个三角形相似的简单方法?
提出你的猜想.
三边对应成比例
两个角分别相等
两边成比例,夹角相等
类比猜想
SSS
AAS、ASA
SAS
新课导入
活动二、抓住“本质”,类比猜想
我们可以用什么办法说明“三边
成比例的两个三角形相似”呢?
思考:
新课导入
活动二、抓住“本质”,类比猜想
探究:任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍.度量这两个三角形的角,它们分别相等吗?这两个三角形相似吗?与同学交流一下,看看是否有同样的结论.
新课讲授
活动一、画图探究,初步感知
如何证明“三边成比例的两个三角形相似”呢?
通过动手实践、培养几何直观
通过摆图感受中介三角形的作用
借助基本图形将定理具体化、直观化,将未知转化为已知
新课讲授
活动二、动手演示,直观感受
1.怎样证明“三边成比例的两个三角形相似”呢?结合图形写出已知、求证、证明过程.
活动三、构造中介,证明定理
新课讲授
A
B
C
求证:△A′B′C′ ∽△ABC
思路点拨:证相似可以转化为我们学行法证相似.
证明:
在线段 AB (或延长线) 上截取 AD=A′B′,过点 D作 DE∥BC 交AC于点 E
A
B
C
D
E
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴ DE=B′C′,EA=CA′.
∴△ADE≌△A′B′C′,
∴△A′B′C′ ∽△ABC
新课讲授
活动三、构造中介,证明定理
几何语言:在△A′B′C′和△ABC中
新课讲授
活动三、构造中介,证明定理
A
B
C
∴△A′B′C′ ∽△ABC
合作探究:三角形全等有“SAS”的判定方法,类似地,两边成比例且夹角相等能否判定两个三角形相似?若成立,试着说说证明过程并写出几何语言.
活动四、类比实验,自主探究
新课讲授
A
B
C
活动四、类比实验,自主探究
新课讲授
已知:在△A′B′C′ 和△ABC中,
求证:△A′B′C′ ∽△ABC
A
B
C
证明:
在线段 AB (或延长线) 上截取 AD=A′B′,过点 D作 DE∥BC 交AC于点 E
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴△ADE≌△A′B′C′,
∴△A′B′C′ ∽△ABC
∴△A′B′C′ ∽△ABC
若在△A′B′C′ 和△ABC中,
△A′B′C′ 与△ABC相似吗?
A
B
C
新课讲授
活动四、类比实验,自主探究
新课讲授
活动五 运用结论 解决问题
例1.根据下列条件,判断△ABC与△A′B′C′ 是否相似,并说明理由:
(1)AB=4cm,BC=6cm,AC=8cm,
A′B′=12cm,B′C′=18cm, A′C′=24′ cm;
(2) ∠A=120°,AB=7cm,AC=14cm,
∠ A′=120°, A′B′=3cm, A′C′=6cm
新课讲授
活动五 运用结论 解决问题
问题1:利用三边判断两个三角形相似的三个步骤:
(1)先排列三边大小顺序;
(2)分别计算边长的比值;
(3)通过比值是否相等判断相似.
并关注问题
问题2中的角是否为两边的夹角.
,
,
∴ △A′B′C′ ∽△ABC
又∠A=∠A′.
∴ △A′B′C′ ∽△ABC
2.如图,能使△ABC∽△ACD的条件是( )
课堂练习
1.教材34页1、2、3题.
点拨:
判定三角形相似,当题目中有公共角时,我们要考虑两边成比例且夹角相等这个判定方法,并且必须保证夹公共角的两边成比例.
D
课堂练习
∴△ABC ∽△DBE
一般性策略: 做什么 如何做 尝试做
强化
弱化
猜想
证明
归纳
本原
课堂小结
A组:教材42页3题
布置作业
B组:1.如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是 ( )
A. △PAB∽△PCA B. △PAB∽△PDA
C. △ABC∽△DBA D. △ABC∽△DCA
C
2.如图,四边形ABCD、四边形CDEF和四边形EFGH是边长相等的正方形.
(1)
(2)求
布置作业
第二十七章 相似
27.2.1 相似三角形的判定 第2课时
学习目标
掌握“三边成比例的两个三角形相似”和“两边成比例且夹角相等的两个三角形相似”的判定定理,并能解决简单问题.(重点)
判定定理“三边成比例的两个三角形相似”的证明.(难点)
新课导入
活动一、复习“旧知”,关联“新知”
1.现在我们已经学过哪些判定两个三角形相似的方法?
(1). 定义法:若△ABC与△A′B′C′ 满足:
△ABC∽△A' B ' C '
(2).平行推相似:
DE∥BC
△ABC∽△ADE
新课导入
活动一、复习“旧知”,关联“新知”
2.在△ABC中,DE∥BC,且DE分别交AB,AC于点D、E,AD=2, BD=4,
BC=6,则DE= .
A
D
E
C
B
2
新课导入
活动二、抓住“本质”,类比猜想
1.一般三角形全等的判定方法有什么?
2.全等是相似比为1的特殊情形,类比判定两个三角形
全等的方法,是否有判定两个三角形相似的简单方法?
提出你的猜想.
三边对应成比例
两个角分别相等
两边成比例,夹角相等
类比猜想
SSS
AAS、ASA
SAS
新课导入
活动二、抓住“本质”,类比猜想
我们可以用什么办法说明“三边
成比例的两个三角形相似”呢?
思考:
新课导入
活动二、抓住“本质”,类比猜想
探究:任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍.度量这两个三角形的角,它们分别相等吗?这两个三角形相似吗?与同学交流一下,看看是否有同样的结论.
新课讲授
活动一、画图探究,初步感知
如何证明“三边成比例的两个三角形相似”呢?
通过动手实践、培养几何直观
通过摆图感受中介三角形的作用
借助基本图形将定理具体化、直观化,将未知转化为已知
新课讲授
活动二、动手演示,直观感受
1.怎样证明“三边成比例的两个三角形相似”呢?结合图形写出已知、求证、证明过程.
活动三、构造中介,证明定理
新课讲授
A
B
C
求证:△A′B′C′ ∽△ABC
思路点拨:证相似可以转化为我们学行法证相似.
证明:
在线段 AB (或延长线) 上截取 AD=A′B′,过点 D作 DE∥BC 交AC于点 E
A
B
C
D
E
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴ DE=B′C′,EA=CA′.
∴△ADE≌△A′B′C′,
∴△A′B′C′ ∽△ABC
新课讲授
活动三、构造中介,证明定理
几何语言:在△A′B′C′和△ABC中
新课讲授
活动三、构造中介,证明定理
A
B
C
∴△A′B′C′ ∽△ABC
合作探究:三角形全等有“SAS”的判定方法,类似地,两边成比例且夹角相等能否判定两个三角形相似?若成立,试着说说证明过程并写出几何语言.
活动四、类比实验,自主探究
新课讲授
A
B
C
活动四、类比实验,自主探究
新课讲授
已知:在△A′B′C′ 和△ABC中,
求证:△A′B′C′ ∽△ABC
A
B
C
证明:
在线段 AB (或延长线) 上截取 AD=A′B′,过点 D作 DE∥BC 交AC于点 E
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴△ADE≌△A′B′C′,
∴△A′B′C′ ∽△ABC
∴△A′B′C′ ∽△ABC
若在△A′B′C′ 和△ABC中,
△A′B′C′ 与△ABC相似吗?
A
B
C
新课讲授
活动四、类比实验,自主探究
新课讲授
活动五 运用结论 解决问题
例1.根据下列条件,判断△ABC与△A′B′C′ 是否相似,并说明理由:
(1)AB=4cm,BC=6cm,AC=8cm,
A′B′=12cm,B′C′=18cm, A′C′=24′ cm;
(2) ∠A=120°,AB=7cm,AC=14cm,
∠ A′=120°, A′B′=3cm, A′C′=6cm
新课讲授
活动五 运用结论 解决问题
问题1:利用三边判断两个三角形相似的三个步骤:
(1)先排列三边大小顺序;
(2)分别计算边长的比值;
(3)通过比值是否相等判断相似.
并关注问题
问题2中的角是否为两边的夹角.
,
,
∴ △A′B′C′ ∽△ABC
又∠A=∠A′.
∴ △A′B′C′ ∽△ABC
2.如图,能使△ABC∽△ACD的条件是( )
课堂练习
1.教材34页1、2、3题.
点拨:
判定三角形相似,当题目中有公共角时,我们要考虑两边成比例且夹角相等这个判定方法,并且必须保证夹公共角的两边成比例.
D
课堂练习
∴△ABC ∽△DBE
一般性策略: 做什么 如何做 尝试做
强化
弱化
猜想
证明
归纳
本原
课堂小结
A组:教材42页3题
布置作业
B组:1.如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是 ( )
A. △PAB∽△PCA B. △PAB∽△PDA
C. △ABC∽△DBA D. △ABC∽△DCA
C
2.如图,四边形ABCD、四边形CDEF和四边形EFGH是边长相等的正方形.
(1)
(2)求
布置作业
