初中数学人教版九下27.2.2相似三角形的性质 课件(共24张PPT)
文档属性
| 名称 | 初中数学人教版九下27.2.2相似三角形的性质 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 541.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 08:25:57 | ||
图片预览





文档简介
(共24张PPT)
第二十七章 相似
27.2.2 相似三角形的性质
教学目标
1.相似三角形对应线段的比、面积的比与相似比的关系的探究与应用. 【难点】
2.提出三角形相似性质的猜想【难点】
学习目标
3. 对于相似三角形,我们已经研究了它的定义和判定.根据已有的研究几何图形的经验,我们还需研究什么?
1.相似三角形的定义是什么?相似比是什么?
2. 相似三角形的判定方法是什么?
新课导入
活动一:提出猜想 确定方向
3.我们可否类比三角形研究思路,研究一下相似三角形的性质?相似三角形的这些几何量可能存在什么性质呢?
1.我们已经学习了相似三角形的哪些性质?
2.我们还可以继续研究相似三角形的哪些几何量的关系?
追问:在三角形的学习过程中,我们知道三角形中有各种各样的几何量,除了边、角,还有什么重要的几何量?
新课讲授
活动二:示范引领 启发思路
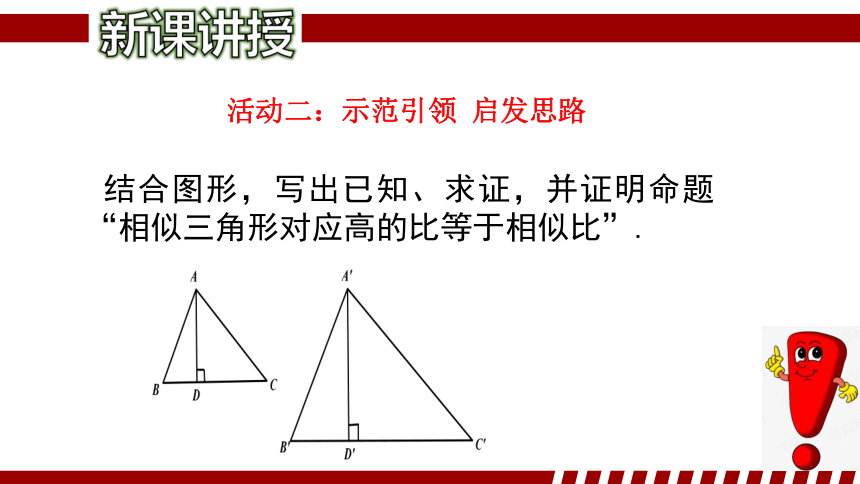
结合图形,写出已知、求证,并证明命题“相似三角形对应高的比等于相似比”.
新课讲授
活动二:示范引领 启发思路
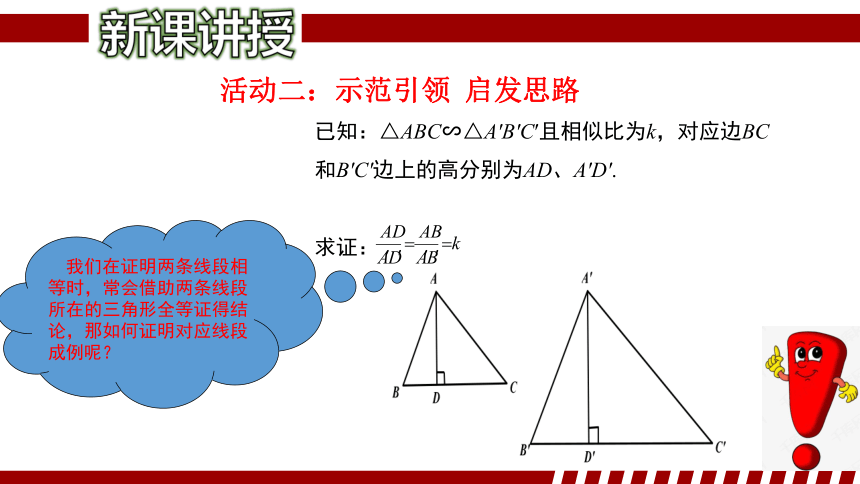
已知:△ABC∽△A′B′C′且相似比为k,对应边BC
和B′C′边上的高分别为AD、A′D′.
求证:
我们在证明两条线段相等时,常会借助两条线段所在的三角形全等证得结论,那如何证明对应线段成例呢?
新课讲授
活动二:示范引领 启发思路
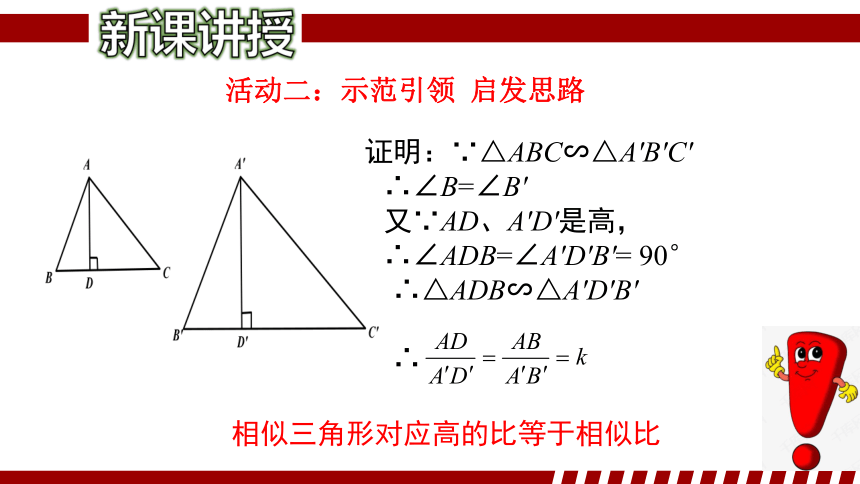
证明:∵△ABC∽△A′B′C′
∴∠B=∠B′
又∵AD、A′D′是高,
∴∠ADB=∠A′D′B′= 90°
∴△ADB∽△A′D′B′
∴
新课讲授
相似三角形对应高的比等于相似比
新课讲授
活动二:示范引领 启发思路
问题2:能否类比证明“相似三角形对应高的比等于相似比”的方法,证明一下相似三角形对应中线的比、对应角平分线的比也等于相似比?归纳你的结论.
新课讲授
活动二:示范引领 启发思路
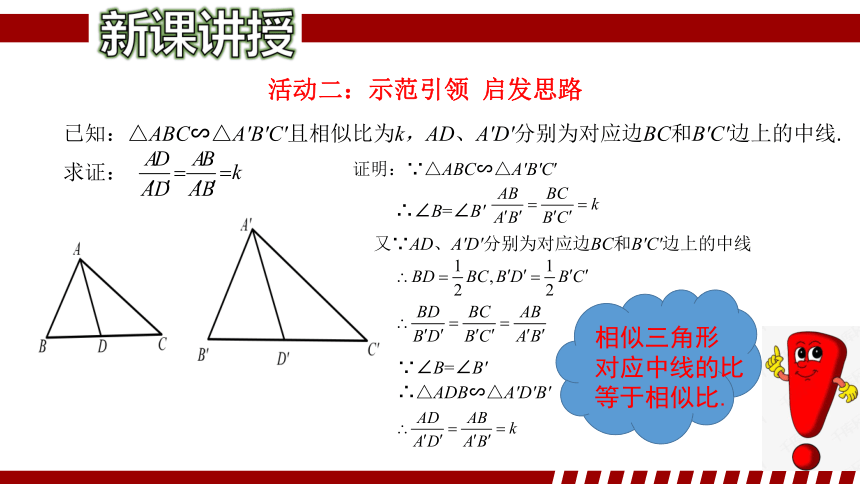
已知:△ABC∽△A′B′C′且相似比为k,AD、A′D′分别为对应边BC和B′C′边上的中线.
求证:
证明:∵△ABC∽△A′B′C′
∴∠B=∠B′
又∵AD、A′D′分别为对应边BC和B′C′边上的中线
∵∠B=∠B′
∴△ADB∽△A′D′B′
相似三角形
对应中线的比
等于相似比.
新课讲授
活动二:示范引领 启发思路
已知:△ABC∽△A′B′C′且相似比为k,AD、A′D′分别为对应角∠BAC,∠B′A′C′的角平分线
求证:
证明:∵△ABC∽△A′B′C′
∴∠B=∠B′,∠BAC=∠B′A′C′
又∵AD、A′D′分别为对应角∠BAC,∠B′A′C′的角平分线,
∴△ADB∽△A′D′B′
相似三角形
对应角平分线
的比等于
相似比.
新课讲授
活动二:示范引领 启发思路
归纳:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般的,我们有:相似三角形对应线段的比等于相似比.
活动三:合作探究 归纳结论
新课讲授
合作探究:在以上数学活动经验基础上,尝试证明相似三角形对应周长、对应面积的比与相似比的关系,并与你的同伴分享你的结论.
相似三角形面积的比
等于相似比吗?
新课讲授
活动三:合作探究 归纳结论
已知:△ABC∽△A′B′C′且相似比为k.
求证:
证明:∵△ABC∽△A′B′C′且相似比为k.
相似三角形周长的比等于相似比.
活动三:合作探究 归纳结论
∴
K2
相似三角形面积的比等于相似比的平方.
新课讲授
证明:∵△ABC∽△A′B′C′
∴即AD=kA′D′ BC=kB′C′
活动三:合作探究 归纳结论
新课讲授
归纳:相似三角形周长的比等于相似比.
相似三角形面积的比等于相似比的平方.
活动四:精讲例题 巩固新知
例题:在△ABC和△DEF中AB=2DE,AC=2DF,∠A=∠D,若△ABC的
边BC上的高为6,面积为
,求△DEF的边EF上的高和面积..
解:∵AB=2DE,AC=2DF ∴
∵∠A=∠D ∴ΔABC∽ΔDEF
∵ΔABC的边BC上的高为6,面积为
∴ΔDEF的边EF上的高为
× 6=3,面积为
=
新课讲授
新课讲授
例:如图所示,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E,F分别在AB,AC上,AD交EF于点H.
活动四:精讲例题 巩固新知
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大,最大值是多少?
新课讲授
活动四:精讲例题 巩固新知
解:(1)在矩形EFPQ中, EF=PQ
∵EF∥PQ,∴△AEF∽△ABC
∵AD⊥BC
∴AD⊥EF于H
(2) ∵在△ABC中, BC=10,高AD=8,EF=x
<0
1.教材39页1.2.3
2. 已知△ABC∽△A B C ,AD、 分别是对应边BC、 上的高,
若BC=8 cm,B C =6 cm,AD=4 cm,则 等于( )
A. 16 cm B. 12 cm C. 3 cm D. 6 cm
3、两个相似三角形对应高的比为3∶7,它们的对应角平分线的比
为( )
A. 7∶3 B. 49∶9 C. 9∶49 D. 3∶7
C
D
课堂练习
4、如图,ΔABC的面积为25,直线DE平行于BC分别交AB、AC于点D、E.
(1)如果ΔADE的面积为9, = .
(2) DE把ΔABC分成面积相等的两部分, .
课堂练习
谈谈这节课的收获是什么?
课堂小结
A组:教材57页4、5,58页10.
B组:1.如图在△ABC中,点D和E分别是边AB和AC的中点,连接DE、DC、BE交于点O,若△ODE的面积时1,则△ABC的面积为( )
A.6 B.9 C.12 D.13.5
C
作业布置
2.等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小
的三角形面积1,△ABC的面积为44,则四边形DBCE的面积是( )
D
A. 22 B. 24 C. 26 D. 28
作业布置
3.有一块三角形余料ABC,它的边BC=120 mm,高AD=80 mm.如图1,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求加工成的正方形零件的边长.
(2)如果要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形组成,如图2,此时,这个矩形零件的两条边长分别为多少
(3)如果要加工的零件只是一个矩形,如图3,此时,这个矩形零件的两条边长不能确定,但这个矩形的面积有最大值,求面积达到最大值时矩形零件的两条边长.
作业布置
第二十七章 相似
27.2.2 相似三角形的性质
教学目标
1.相似三角形对应线段的比、面积的比与相似比的关系的探究与应用. 【难点】
2.提出三角形相似性质的猜想【难点】
学习目标
3. 对于相似三角形,我们已经研究了它的定义和判定.根据已有的研究几何图形的经验,我们还需研究什么?
1.相似三角形的定义是什么?相似比是什么?
2. 相似三角形的判定方法是什么?
新课导入
活动一:提出猜想 确定方向
3.我们可否类比三角形研究思路,研究一下相似三角形的性质?相似三角形的这些几何量可能存在什么性质呢?
1.我们已经学习了相似三角形的哪些性质?
2.我们还可以继续研究相似三角形的哪些几何量的关系?
追问:在三角形的学习过程中,我们知道三角形中有各种各样的几何量,除了边、角,还有什么重要的几何量?
新课讲授
活动二:示范引领 启发思路
结合图形,写出已知、求证,并证明命题“相似三角形对应高的比等于相似比”.
新课讲授
活动二:示范引领 启发思路
已知:△ABC∽△A′B′C′且相似比为k,对应边BC
和B′C′边上的高分别为AD、A′D′.
求证:
我们在证明两条线段相等时,常会借助两条线段所在的三角形全等证得结论,那如何证明对应线段成例呢?
新课讲授
活动二:示范引领 启发思路
证明:∵△ABC∽△A′B′C′
∴∠B=∠B′
又∵AD、A′D′是高,
∴∠ADB=∠A′D′B′= 90°
∴△ADB∽△A′D′B′
∴
新课讲授
相似三角形对应高的比等于相似比
新课讲授
活动二:示范引领 启发思路
问题2:能否类比证明“相似三角形对应高的比等于相似比”的方法,证明一下相似三角形对应中线的比、对应角平分线的比也等于相似比?归纳你的结论.
新课讲授
活动二:示范引领 启发思路
已知:△ABC∽△A′B′C′且相似比为k,AD、A′D′分别为对应边BC和B′C′边上的中线.
求证:
证明:∵△ABC∽△A′B′C′
∴∠B=∠B′
又∵AD、A′D′分别为对应边BC和B′C′边上的中线
∵∠B=∠B′
∴△ADB∽△A′D′B′
相似三角形
对应中线的比
等于相似比.
新课讲授
活动二:示范引领 启发思路
已知:△ABC∽△A′B′C′且相似比为k,AD、A′D′分别为对应角∠BAC,∠B′A′C′的角平分线
求证:
证明:∵△ABC∽△A′B′C′
∴∠B=∠B′,∠BAC=∠B′A′C′
又∵AD、A′D′分别为对应角∠BAC,∠B′A′C′的角平分线,
∴△ADB∽△A′D′B′
相似三角形
对应角平分线
的比等于
相似比.
新课讲授
活动二:示范引领 启发思路
归纳:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
一般的,我们有:相似三角形对应线段的比等于相似比.
活动三:合作探究 归纳结论
新课讲授
合作探究:在以上数学活动经验基础上,尝试证明相似三角形对应周长、对应面积的比与相似比的关系,并与你的同伴分享你的结论.
相似三角形面积的比
等于相似比吗?
新课讲授
活动三:合作探究 归纳结论
已知:△ABC∽△A′B′C′且相似比为k.
求证:
证明:∵△ABC∽△A′B′C′且相似比为k.
相似三角形周长的比等于相似比.
活动三:合作探究 归纳结论
∴
K2
相似三角形面积的比等于相似比的平方.
新课讲授
证明:∵△ABC∽△A′B′C′
∴即AD=kA′D′ BC=kB′C′
活动三:合作探究 归纳结论
新课讲授
归纳:相似三角形周长的比等于相似比.
相似三角形面积的比等于相似比的平方.
活动四:精讲例题 巩固新知
例题:在△ABC和△DEF中AB=2DE,AC=2DF,∠A=∠D,若△ABC的
边BC上的高为6,面积为
,求△DEF的边EF上的高和面积..
解:∵AB=2DE,AC=2DF ∴
∵∠A=∠D ∴ΔABC∽ΔDEF
∵ΔABC的边BC上的高为6,面积为
∴ΔDEF的边EF上的高为
× 6=3,面积为
=
新课讲授
新课讲授
例:如图所示,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E,F分别在AB,AC上,AD交EF于点H.
活动四:精讲例题 巩固新知
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大,最大值是多少?
新课讲授
活动四:精讲例题 巩固新知
解:(1)在矩形EFPQ中, EF=PQ
∵EF∥PQ,∴△AEF∽△ABC
∵AD⊥BC
∴AD⊥EF于H
(2) ∵在△ABC中, BC=10,高AD=8,EF=x
<0
1.教材39页1.2.3
2. 已知△ABC∽△A B C ,AD、 分别是对应边BC、 上的高,
若BC=8 cm,B C =6 cm,AD=4 cm,则 等于( )
A. 16 cm B. 12 cm C. 3 cm D. 6 cm
3、两个相似三角形对应高的比为3∶7,它们的对应角平分线的比
为( )
A. 7∶3 B. 49∶9 C. 9∶49 D. 3∶7
C
D
课堂练习
4、如图,ΔABC的面积为25,直线DE平行于BC分别交AB、AC于点D、E.
(1)如果ΔADE的面积为9, = .
(2) DE把ΔABC分成面积相等的两部分, .
课堂练习
谈谈这节课的收获是什么?
课堂小结
A组:教材57页4、5,58页10.
B组:1.如图在△ABC中,点D和E分别是边AB和AC的中点,连接DE、DC、BE交于点O,若△ODE的面积时1,则△ABC的面积为( )
A.6 B.9 C.12 D.13.5
C
作业布置
2.等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小
的三角形面积1,△ABC的面积为44,则四边形DBCE的面积是( )
D
A. 22 B. 24 C. 26 D. 28
作业布置
3.有一块三角形余料ABC,它的边BC=120 mm,高AD=80 mm.如图1,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求加工成的正方形零件的边长.
(2)如果要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形组成,如图2,此时,这个矩形零件的两条边长分别为多少
(3)如果要加工的零件只是一个矩形,如图3,此时,这个矩形零件的两条边长不能确定,但这个矩形的面积有最大值,求面积达到最大值时矩形零件的两条边长.
作业布置
