初中数学人教版九下27.2.3相似三角形应用举例第2课时 课件(共18张PPT)
文档属性
| 名称 | 初中数学人教版九下27.2.3相似三角形应用举例第2课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 08:27:45 | ||
图片预览



文档简介
(共18张PPT)
第二十七章 相似
27.2.3 相似三角形的应用举例 第2课时
运用相似三角形有关知识,解决不能直接测量的物体的长度和高度等一些实际问题. 【重点】
从实现遮挡问题中抽象出相似模型. 【难点】
学习目标
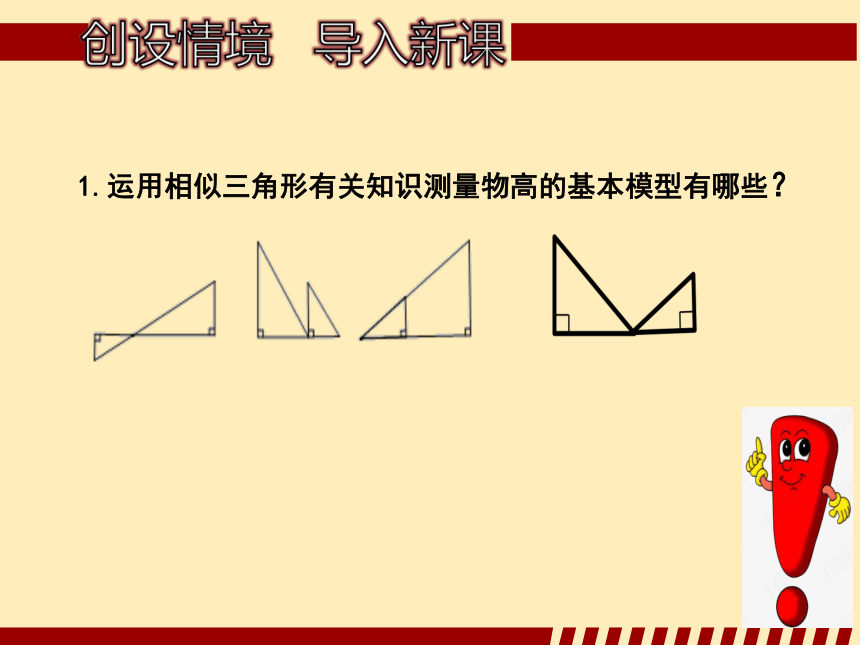
1.运用相似三角形有关知识测量物高的基本模型有哪些?
创设情境 导入新课
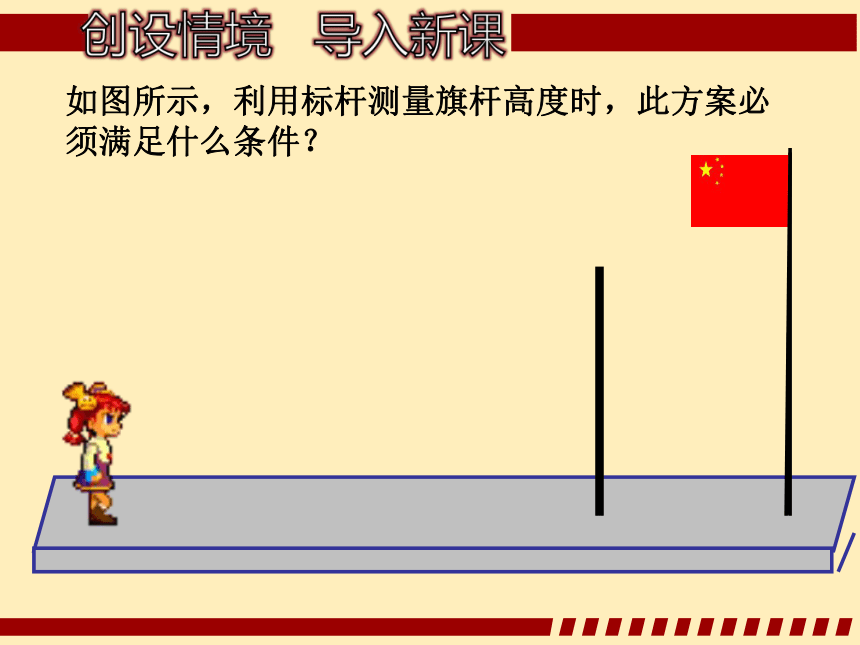
如图所示,利用标杆测量旗杆高度时,此方案必须满足什么条件?
创设情境 导入新课
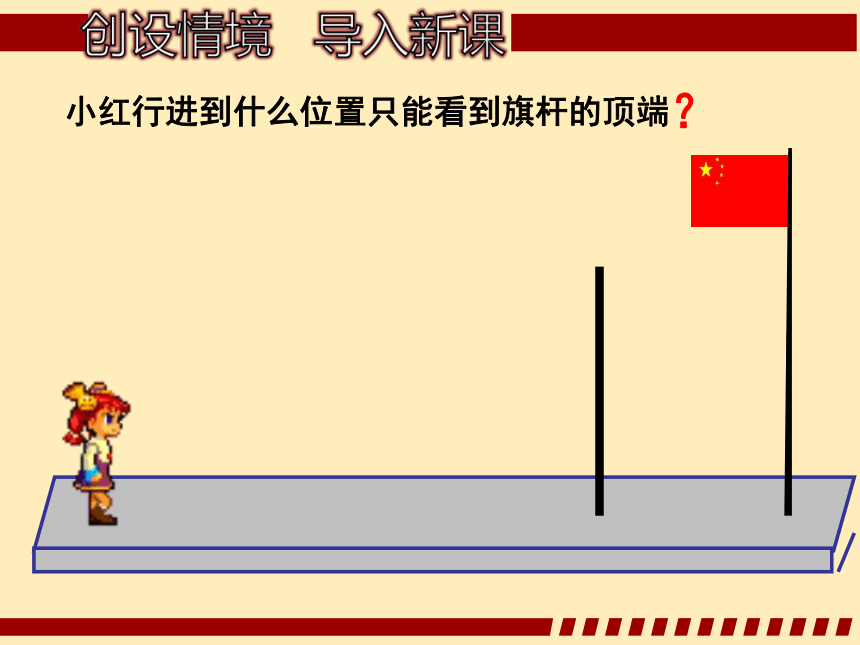
小红行进到什么位置只能看到旗杆的顶端?
创设情境 导入新课
A
C
1
G
如图所示,利用标杆测量旗杆高度时,此方案必须满足什么条件?
创设情境 导入新课
A
C
E
B
F
D
H
3
M
N
1
2
怎么办?
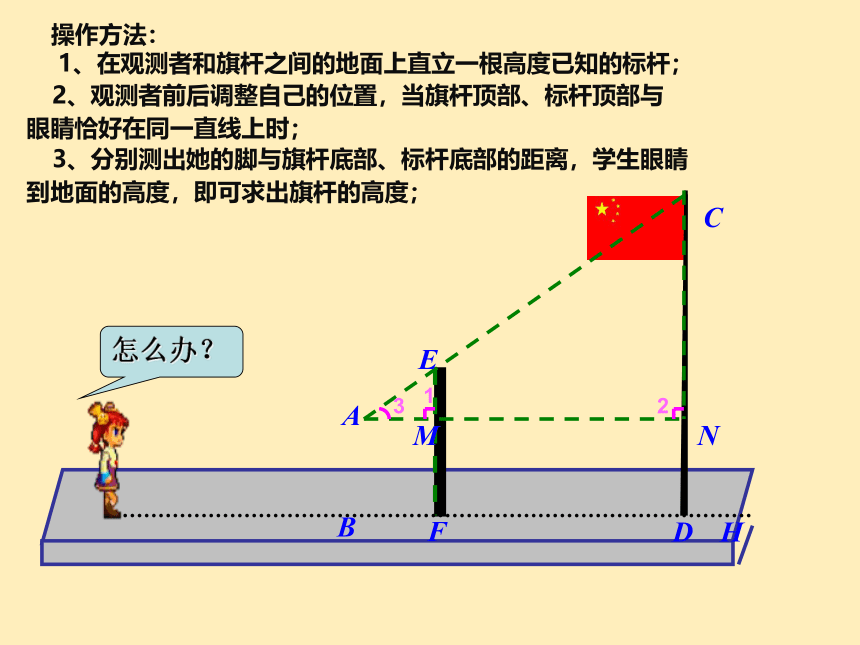
3、分别测出她的脚与旗杆底部、标杆底部的距离,学生眼睛到地面的高度,即可求出旗杆的高度;
操作方法:
1、在观测者和旗杆之间的地面上直立一根高度已知的标杆;
2、观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时;
例:如图,左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树底部的距离BD=5m,一个人估计自己的眼睛距地面1.6m.她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶点C了?
B
D
C
A
F
1.此人行进到什么位置只能看到右边较高的树的顶端点C了?
2.构建相似模型,将实际问题转化为数学问题,试着写出解题过程.
精讲例题 强化重点
(二)精讲例题 强化重点
解:如图所示,当E、A、C在一条直线上时
∵AB⊥l , CD⊥l
∴AB∥CD
∴△AEH∽△CEK
∴
解得 EH=8
试着归纳一下用相似三角形解决实际问题时的一般步骤.
图中找相似,相似得比例,
比例来计算,计算求线段.
(三)当堂检测 巩固新知
200
1.如图是步枪在瞄准时的示意图,从眼睛到
准星的距离OE为80cm,步枪上的准星宽度AB
为0.2cm,目标的正面宽度CD为50cm,则眼睛
到目标的距离OF为______m.
200
(三)当堂检测 巩固新知
36
2.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 米.
(三)当堂检测 巩固新知
7.3
3.某天小明和小亮去某影视基地游玩,当小明给站在城楼上
的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点
恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,
凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼
底部的距离为40米,小亮身高为1.7米,那么城楼的高
度为 米.
7.3
(三)当堂检测 巩固新知
4.王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.两个路灯之间的距离为 ( )米;
当王华同学走到路灯BD处时,他在路灯AC下的影子长是( )米
18
3.6
课堂小结
这节课我们学到了什么?
1.如何解决不能直接测量的物体的长度和高度的实际问题?
2.学习过程中体现了怎样的数学思想
作业布置
A组: 1.为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E、C、A三点共线,则旗杆AB的高度为( )
A.13.5米 B.12.5米 C.11.9米 D.10.5米
A
作业布置
2.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
作业布置
B组:1.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,出南门 步恰好看到位于A处的树木(即点D在直线AC上).
作业布置
2. 某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=1.2米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.8米, CG=20米,请你根据以上数据,估算古塔的高度AB.
第二十七章 相似
27.2.3 相似三角形的应用举例 第2课时
运用相似三角形有关知识,解决不能直接测量的物体的长度和高度等一些实际问题. 【重点】
从实现遮挡问题中抽象出相似模型. 【难点】
学习目标
1.运用相似三角形有关知识测量物高的基本模型有哪些?
创设情境 导入新课
如图所示,利用标杆测量旗杆高度时,此方案必须满足什么条件?
创设情境 导入新课
小红行进到什么位置只能看到旗杆的顶端?
创设情境 导入新课
A
C
1
G
如图所示,利用标杆测量旗杆高度时,此方案必须满足什么条件?
创设情境 导入新课
A
C
E
B
F
D
H
3
M
N
1
2
怎么办?
3、分别测出她的脚与旗杆底部、标杆底部的距离,学生眼睛到地面的高度,即可求出旗杆的高度;
操作方法:
1、在观测者和旗杆之间的地面上直立一根高度已知的标杆;
2、观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时;
例:如图,左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树底部的距离BD=5m,一个人估计自己的眼睛距地面1.6m.她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶点C了?
B
D
C
A
F
1.此人行进到什么位置只能看到右边较高的树的顶端点C了?
2.构建相似模型,将实际问题转化为数学问题,试着写出解题过程.
精讲例题 强化重点
(二)精讲例题 强化重点
解:如图所示,当E、A、C在一条直线上时
∵AB⊥l , CD⊥l
∴AB∥CD
∴△AEH∽△CEK
∴
解得 EH=8
试着归纳一下用相似三角形解决实际问题时的一般步骤.
图中找相似,相似得比例,
比例来计算,计算求线段.
(三)当堂检测 巩固新知
200
1.如图是步枪在瞄准时的示意图,从眼睛到
准星的距离OE为80cm,步枪上的准星宽度AB
为0.2cm,目标的正面宽度CD为50cm,则眼睛
到目标的距离OF为______m.
200
(三)当堂检测 巩固新知
36
2.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 米.
(三)当堂检测 巩固新知
7.3
3.某天小明和小亮去某影视基地游玩,当小明给站在城楼上
的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点
恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,
凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼
底部的距离为40米,小亮身高为1.7米,那么城楼的高
度为 米.
7.3
(三)当堂检测 巩固新知
4.王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.两个路灯之间的距离为 ( )米;
当王华同学走到路灯BD处时,他在路灯AC下的影子长是( )米
18
3.6
课堂小结
这节课我们学到了什么?
1.如何解决不能直接测量的物体的长度和高度的实际问题?
2.学习过程中体现了怎样的数学思想
作业布置
A组: 1.为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E、C、A三点共线,则旗杆AB的高度为( )
A.13.5米 B.12.5米 C.11.9米 D.10.5米
A
作业布置
2.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
作业布置
B组:1.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,出南门 步恰好看到位于A处的树木(即点D在直线AC上).
作业布置
2. 某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得EC=1.2米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得FG=1.8米, CG=20米,请你根据以上数据,估算古塔的高度AB.
