初中数学人教版九下27.3位似第2课时 课件(共20张PPT)
文档属性
| 名称 | 初中数学人教版九下27.3位似第2课时 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 796.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 08:30:16 | ||
图片预览




文档简介
(共20张PPT)
第二十七章 相似
27.3 位似
学习目标
探究平面直角坐标系中,以原点为位似中心的位似图形的对应点的坐标之间的关系【重、难点】
新课导入
1.如图所示,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-3,2),B(-1,3)C(-1,1).
(1)将△ABC向右平移4个单位长度得到△A1B1C1,写出A1、B1、C1三点的坐标.
(2)写出△ABC关于y轴对称的△A2B2C2的三个顶点A2、B2、C2的坐标.
(3) 写出△ABC关于原点中心对称的△A3B3C3的三个顶点A3、B3、C3的坐标
新课讲授
活动一 动手画图 归纳结论
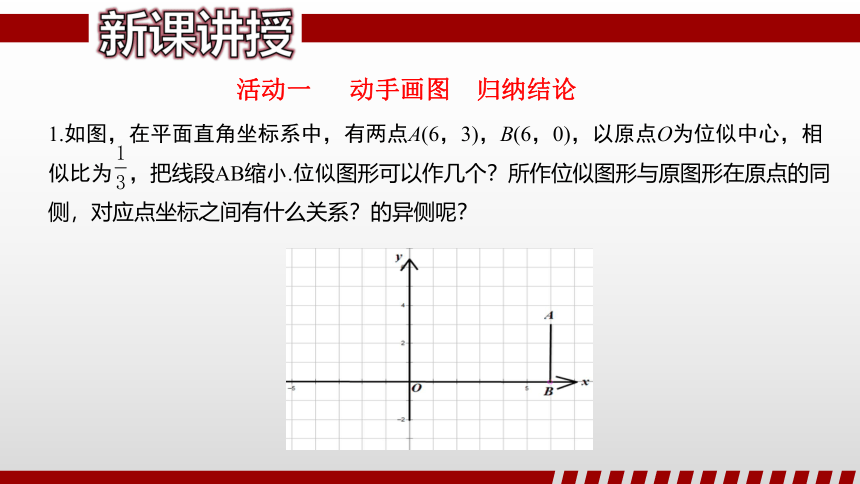
1.如图,在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,把线段AB缩小.位似图形可以作几个?所作位似图形与原图形在原点的同侧,对应点坐标之间有什么关系?的异侧呢?
新课讲授
A′
B′
A′′
A′′
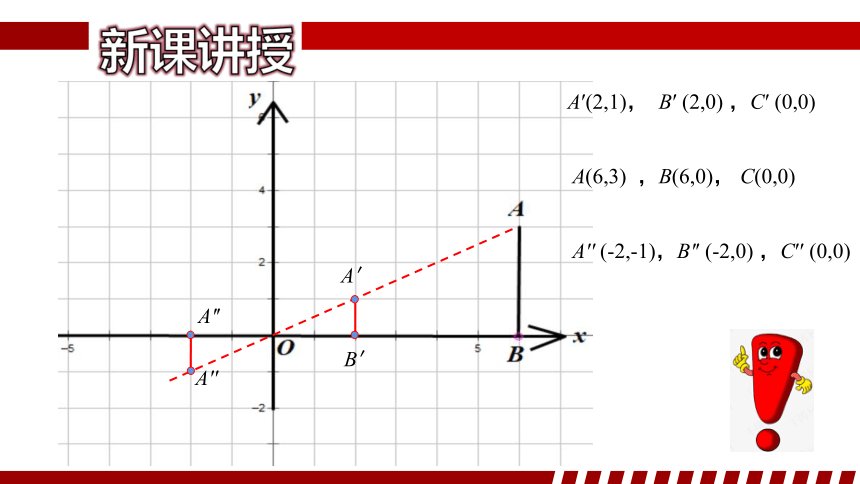
A(6,3) ,B(6,0), C(0,0)
A′(2,1), B′ (2,0) ,C′ (0,0)
A′′ (-2,-1),B′′ (-2,0) ,C′′ (0,0)
新课讲授
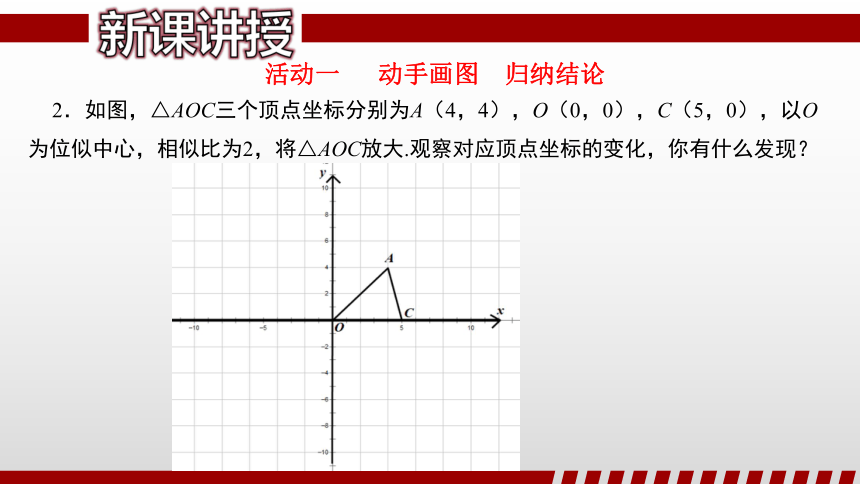
2.如图,△AOC三个顶点坐标分别为A(4,4),O(0,0),C(5,0),以O为位似中心,相似比为2,将△AOC放大.观察对应顶点坐标的变化,你有什么发现?
活动一 动手画图 归纳结论
新课讲授
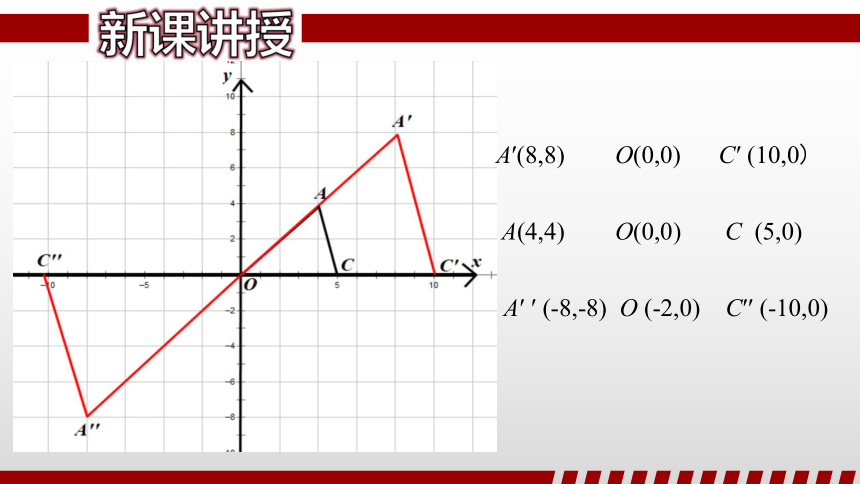
A(4,4) O(0,0) C (5,0)
A′(8,8) O(0,0) C′ (10,0)
A′ ′ (-8,-8) O (-2,0) C′′ (-10,0)
新课讲授
若在△AOC内部任取一点P(x,y),那么对应位似图形里的对应点坐标是什么?
(2x,2y)或(-2x,-2y)
若在平面直角坐标系中,以原点为位似中心,画一个与原图形位似的图形,使它与原图形的相似比为k,原图形上的点(x,y),对应位似图形上点的坐标为 .
(kx,ky)或(-kx,-ky)
新课讲授
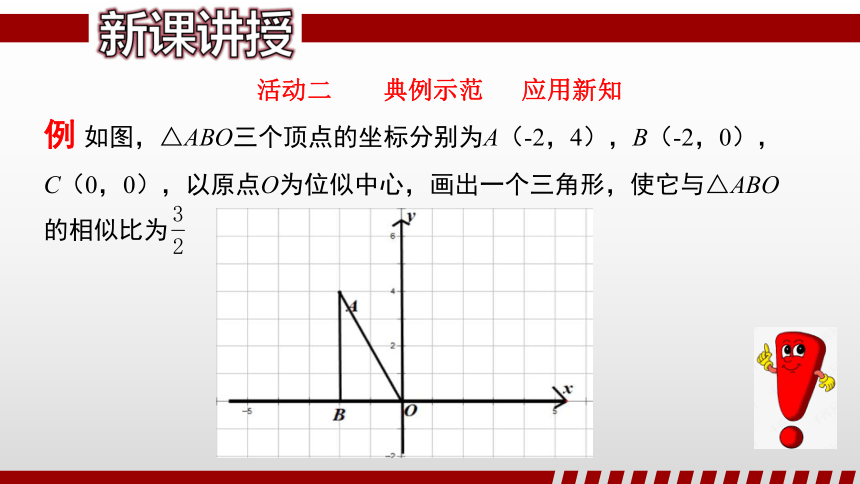
活动二 典例示范 应用新知
例 如图,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),
C(0,0),以原点O为位似中心,画出一个三角形,使它与△ABO
的相似比为
新课讲授
活动二 典例示范 应用新知
1.可以有几种方法确定与△ABO的相似比为
的三角形?比较一下哪种方法更简便.
2. 与△ABO的相似比为 的三角形有几个?
试着说说对应点坐标.
3.在第二象限画图.
新课讲授
活动二 典例示范 应用新知
新课讲授
活动三 拓展延伸 把握本质
例:在网格图中,已知 △ABC 和点 M (1,2).
(1) 以点 M 为位似中心,画出与 △ABC位似比为 2的位似图△A′B′C′;
(2) 写出 △A′B′C′ 的各顶点坐标.
解决问题有几种方法?
温馨提示:M点能否先看作新原点,根据位似图形对应点的坐标之间的规律画图,后在原坐标系读取对应点的坐标?
新课讲授
活动三 拓展延伸 把握本质
A′(3,5),
B′(5,1) ,
C′(11,4)
课堂练习
2.将平面直角坐标系中某个图形的各点坐标做如下变化,
其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变;
B. 将各点的横坐标除以 2,纵坐标不变;
C. 将各点的横坐标、纵坐标都乘以 2;
D. 将各点的纵坐标减去 2,横坐标加上 2 .
C
课堂练习
3.△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以原点O为位似中心,相似比为 ,将△AOB缩小,则点B的对应点B′的坐标是 .
(2,4)或(-2,-4)
4.如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把 E 点弄脏了,则 E 点坐标为 ( )
A
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6)
课堂小结
谈谈这节课的收获
1.在平面直角坐标系中,如何做两个以原点为位似中心的位似图形?有几种方法?
2.在探究平面直角坐标系中,两个以原点为位似中心的位似图形对应点坐标规律时,用到什么数学方法和数学思想?
作业布置
A组:教材51页3、4、5,52页7.
作业布置
B组:
1.如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
D
A.
B.(m,n)
C D
作业布置
2.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A
A.﹣2a+3 B.﹣2a+1 C.﹣2a+2 D.﹣2a﹣2
作业布置
3.按下列要求在如图格点中作图:
(2)以点B为位似中心,作出△ABC放大2倍的图形△BA″C″,则△BA″C″ 的面积为 .
(1)作出△ABC关于原点成中心对称的图形△A'B'C';
14
第二十七章 相似
27.3 位似
学习目标
探究平面直角坐标系中,以原点为位似中心的位似图形的对应点的坐标之间的关系【重、难点】
新课导入
1.如图所示,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-3,2),B(-1,3)C(-1,1).
(1)将△ABC向右平移4个单位长度得到△A1B1C1,写出A1、B1、C1三点的坐标.
(2)写出△ABC关于y轴对称的△A2B2C2的三个顶点A2、B2、C2的坐标.
(3) 写出△ABC关于原点中心对称的△A3B3C3的三个顶点A3、B3、C3的坐标
新课讲授
活动一 动手画图 归纳结论
1.如图,在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,把线段AB缩小.位似图形可以作几个?所作位似图形与原图形在原点的同侧,对应点坐标之间有什么关系?的异侧呢?
新课讲授
A′
B′
A′′
A′′
A(6,3) ,B(6,0), C(0,0)
A′(2,1), B′ (2,0) ,C′ (0,0)
A′′ (-2,-1),B′′ (-2,0) ,C′′ (0,0)
新课讲授
2.如图,△AOC三个顶点坐标分别为A(4,4),O(0,0),C(5,0),以O为位似中心,相似比为2,将△AOC放大.观察对应顶点坐标的变化,你有什么发现?
活动一 动手画图 归纳结论
新课讲授
A(4,4) O(0,0) C (5,0)
A′(8,8) O(0,0) C′ (10,0)
A′ ′ (-8,-8) O (-2,0) C′′ (-10,0)
新课讲授
若在△AOC内部任取一点P(x,y),那么对应位似图形里的对应点坐标是什么?
(2x,2y)或(-2x,-2y)
若在平面直角坐标系中,以原点为位似中心,画一个与原图形位似的图形,使它与原图形的相似比为k,原图形上的点(x,y),对应位似图形上点的坐标为 .
(kx,ky)或(-kx,-ky)
新课讲授
活动二 典例示范 应用新知
例 如图,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),
C(0,0),以原点O为位似中心,画出一个三角形,使它与△ABO
的相似比为
新课讲授
活动二 典例示范 应用新知
1.可以有几种方法确定与△ABO的相似比为
的三角形?比较一下哪种方法更简便.
2. 与△ABO的相似比为 的三角形有几个?
试着说说对应点坐标.
3.在第二象限画图.
新课讲授
活动二 典例示范 应用新知
新课讲授
活动三 拓展延伸 把握本质
例:在网格图中,已知 △ABC 和点 M (1,2).
(1) 以点 M 为位似中心,画出与 △ABC位似比为 2的位似图△A′B′C′;
(2) 写出 △A′B′C′ 的各顶点坐标.
解决问题有几种方法?
温馨提示:M点能否先看作新原点,根据位似图形对应点的坐标之间的规律画图,后在原坐标系读取对应点的坐标?
新课讲授
活动三 拓展延伸 把握本质
A′(3,5),
B′(5,1) ,
C′(11,4)
课堂练习
2.将平面直角坐标系中某个图形的各点坐标做如下变化,
其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 2,横坐标不变;
B. 将各点的横坐标除以 2,纵坐标不变;
C. 将各点的横坐标、纵坐标都乘以 2;
D. 将各点的纵坐标减去 2,横坐标加上 2 .
C
课堂练习
3.△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以原点O为位似中心,相似比为 ,将△AOB缩小,则点B的对应点B′的坐标是 .
(2,4)或(-2,-4)
4.如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把 E 点弄脏了,则 E 点坐标为 ( )
A
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6)
课堂小结
谈谈这节课的收获
1.在平面直角坐标系中,如何做两个以原点为位似中心的位似图形?有几种方法?
2.在探究平面直角坐标系中,两个以原点为位似中心的位似图形对应点坐标规律时,用到什么数学方法和数学思想?
作业布置
A组:教材51页3、4、5,52页7.
作业布置
B组:
1.如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中格点上,若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
D
A.
B.(m,n)
C D
作业布置
2.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A
A.﹣2a+3 B.﹣2a+1 C.﹣2a+2 D.﹣2a﹣2
作业布置
3.按下列要求在如图格点中作图:
(2)以点B为位似中心,作出△ABC放大2倍的图形△BA″C″,则△BA″C″ 的面积为 .
(1)作出△ABC关于原点成中心对称的图形△A'B'C';
14
