初中数学人教版九下28.1 锐角三角函数(第2课时)课件(共25张PPT)
文档属性
| 名称 | 初中数学人教版九下28.1 锐角三角函数(第2课时)课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
28.1 锐角三角函数
(第2课时)
第二十八章 锐角三角函数
学习目标
1.理解余弦、正切等锐角三角函数的概念,会利用定义求三角函数值.(重点)
2.体会锐角三角函数的函数特征.(难点)
新课导入
探究 Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠A',∠A和∠A'的对边与邻边如图所示.
(1) 与 有什么关系?请给出证明.
证明:∵∠C= ∠C'=90°,∠A=∠A'.
∴Rt △ABC ∽Rt △ .
∴ ,
即 .
'
'
'
A B C
解: = .
探究 Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠A',∠A和∠A'的对边与邻边如图所示.
(2) 与 有什么关系?请给出证明.
证明:∵∠C= ∠C'=90°,∠A=∠A'.
∴Rt △ABC ∽Rt △ .
∴ ,
即 .
'
'
'
A B C
解: .
在直角三角形中,当锐角的度数一定时,
无论这个直角三角形大小如何,
它的邻边与斜边的比是一个定值,
它的对边与邻边的比是一个定值.
归纳总结
学习余弦和正切的概念
一
讲授新课
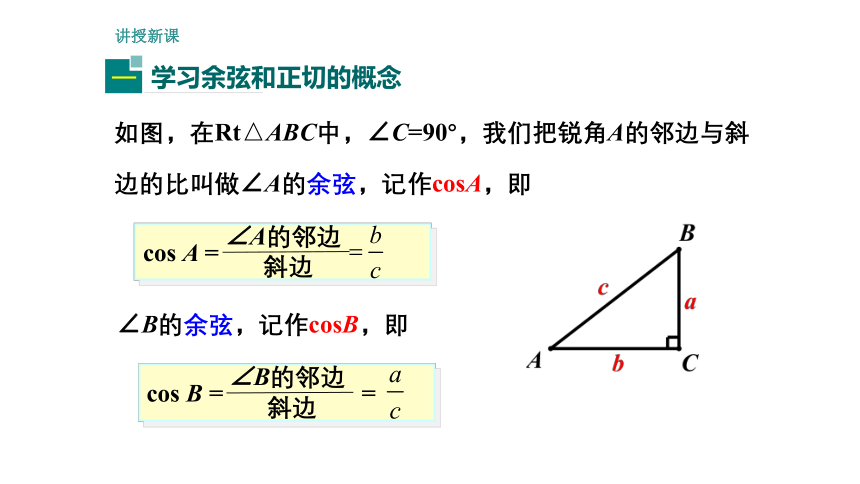
如图,在Rt△ABC中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
∠A的邻边
斜边
cos A =
∠B的邻边
斜边
cos B = =
∠B的余弦,记作cosB,即
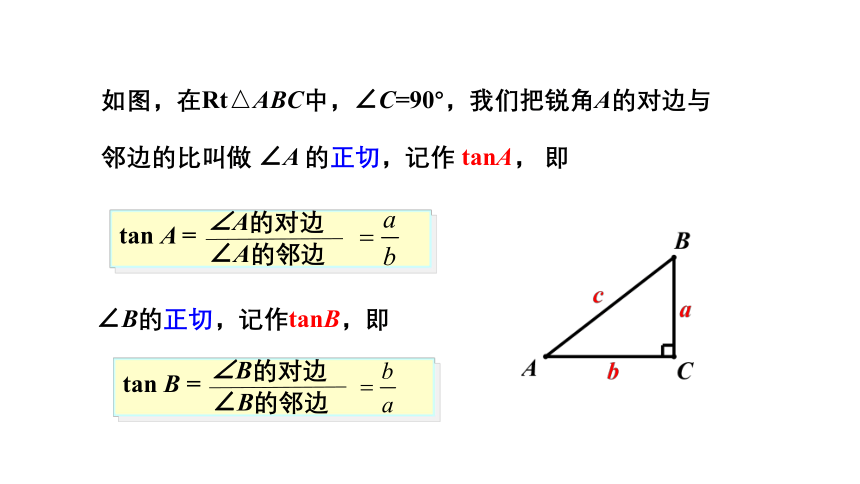
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做 ∠A 的正切,记作 tanA, 即
∠A的对边
∠A的邻边
tan A =
∠B的对边
∠B的邻边
tan B =
∠B的正切,记作tanB,即
探索:我们学习了关于直角三角形中两边比的三个概念分别是什么?它们与三角形的大小有关系吗?与角度的大小有关系吗?有什么关系?
归纳:锐角的正弦、余弦和正切与三角形的大小______关系,与角度的大小 ______关系,随着角度的变化而_______,即对于锐角的每一个确定的值,它的正弦、余弦和正切都有____________的值与之对应,从而形成了______关系,即锐角的正弦、余弦和正切是_________的函数,______________是自变量.
没有
有
变化
唯一确定
函数
这个锐角
锐角(的度数)
学习三角函数的概念
二
命名:锐角的正弦、余弦和正切称为这个锐角的三角函数.
讨论:如果锐角不在直角三角形中,那么它的三角函数值还存在吗?
总结:锐角的三角函数是由锐角的大小决定的,即使不在直角三角形中,它的三角函数依然存在,放在直角三角形中更方便利用定义式求解.
求锐角三角函数的值
三
例2 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理,得
因此
思考:
1.能求∠B的三个三角函数的值吗?
A
B
C
10
6
2.如果改变题目的条件,使三角函数的值不变,那么条件可以怎样改变?从以下角度思考:
(1)换掉一条边长,即只保留“AB=10,BC=6”中的一个条件,再增加另一个条件;
A
B
C
10
6
用“AC=8”换掉“AB=10,BC=6”中的任何一个条件均可.
(2)改变两条边长,即“AB=10,BC=6”两个条件中的数据都改为其他数,有多少种改法,这些不同的改法有什么共同特点?
A
B
C
10
6
有无数种改法,比如:
AB=5,BC=3;
或AB=15,BC=9;
或AB=1,BC=0.6;等等.
这些不同的改法中,AB:BC=5:3.
(3)不给出两条边长的具体数值,可以吗?尝试写出一个符合题意的条件,并进行解答;
A
B
C
把“AB=10,BC=6”改为“AB:BC=5:3”.
解:设AB=5k,则BC=3k,
由勾股定理,得
因此
(4)只给出∠B的一个三角函数值,没有关于边长的条件,可以吗?尝试编题并解答.
A
B
C
例:在 Rt△ABC 中,∠C=90°, 求sinA,cosA,tanA的值
由勾股定理,得
因此
解:由 得,若设AB=5k,则BC=3k,
3.给出∠B的一个三角函数值,以及“AB=10,BC=6”中的一个条件,能求出什么?尝试编题并解答.
能求其他未知的边长和锐角三角函数值.
A
B
C
10
6
例:在 Rt△ABC 中,∠C=90°,BC=6,
求AC,AB以及sinA,cosA,tanA,sinB,tanB的值.
由勾股定理,得
解:由 得,若设AB=5k,则BC=3k,
A
B
C
6
由BC=6,得3k=6,解得k=2,则AB=10.
因此
对比上述两个锐角的三角函数值,发现什么等量关系?为什么会有这种关系?
sinA=cosB,cosA=sinB,tanA·tanB=1.
由锐角的正弦、余弦和正切定义,可知:
A
B
C
1. 教材第65页练习第1-2题.
2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若 BC=4,AB=5,则
sinA=______,cosB=______,tanA=______.
·
A
O
B
C
课堂练习
4. 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,
若 ,
那么 ( )
B
a
O
C
D
B
A
P
3. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,∠A=35°,则直角边 BC 的长是 ( )
A.
B.
C.
D.
A
A
B
C
5. 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,求 sinA,tanA 的值.
解:
A
B
C
设 AC = 15k,则 AB = 17k.
由勾股定理,得
∴
课堂小结
1.综合两节课所学内容,说一下常见的三种锐角三角函数的求法.
2.为什么说锐角三角函数是一种函数,谁是谁的函数?谁是自变量?
3.结合本节课所学内容,谈一下你对类比思想的认识.
正弦
余弦
正切
锐角∠A的
三角函数
布置作业
A组:
1.教材第68页习题28.1第1题(只求余弦值和正切值),第2题.
2.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
B组:
1.教材第70页习题28.1第10题(证明结论).
2. 如图,在△ABC中,AB=AC=4,BC=6. 求cosB,tanC的值.
A
B
C
提示:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.
28.1 锐角三角函数
(第2课时)
第二十八章 锐角三角函数
学习目标
1.理解余弦、正切等锐角三角函数的概念,会利用定义求三角函数值.(重点)
2.体会锐角三角函数的函数特征.(难点)
新课导入
探究 Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠A',∠A和∠A'的对边与邻边如图所示.
(1) 与 有什么关系?请给出证明.
证明:∵∠C= ∠C'=90°,∠A=∠A'.
∴Rt △ABC ∽Rt △ .
∴ ,
即 .
'
'
'
A B C
解: = .
探究 Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠A',∠A和∠A'的对边与邻边如图所示.
(2) 与 有什么关系?请给出证明.
证明:∵∠C= ∠C'=90°,∠A=∠A'.
∴Rt △ABC ∽Rt △ .
∴ ,
即 .
'
'
'
A B C
解: .
在直角三角形中,当锐角的度数一定时,
无论这个直角三角形大小如何,
它的邻边与斜边的比是一个定值,
它的对边与邻边的比是一个定值.
归纳总结
学习余弦和正切的概念
一
讲授新课
如图,在Rt△ABC中,∠C=90°,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
∠A的邻边
斜边
cos A =
∠B的邻边
斜边
cos B = =
∠B的余弦,记作cosB,即
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做 ∠A 的正切,记作 tanA, 即
∠A的对边
∠A的邻边
tan A =
∠B的对边
∠B的邻边
tan B =
∠B的正切,记作tanB,即
探索:我们学习了关于直角三角形中两边比的三个概念分别是什么?它们与三角形的大小有关系吗?与角度的大小有关系吗?有什么关系?
归纳:锐角的正弦、余弦和正切与三角形的大小______关系,与角度的大小 ______关系,随着角度的变化而_______,即对于锐角的每一个确定的值,它的正弦、余弦和正切都有____________的值与之对应,从而形成了______关系,即锐角的正弦、余弦和正切是_________的函数,______________是自变量.
没有
有
变化
唯一确定
函数
这个锐角
锐角(的度数)
学习三角函数的概念
二
命名:锐角的正弦、余弦和正切称为这个锐角的三角函数.
讨论:如果锐角不在直角三角形中,那么它的三角函数值还存在吗?
总结:锐角的三角函数是由锐角的大小决定的,即使不在直角三角形中,它的三角函数依然存在,放在直角三角形中更方便利用定义式求解.
求锐角三角函数的值
三
例2 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理,得
因此
思考:
1.能求∠B的三个三角函数的值吗?
A
B
C
10
6
2.如果改变题目的条件,使三角函数的值不变,那么条件可以怎样改变?从以下角度思考:
(1)换掉一条边长,即只保留“AB=10,BC=6”中的一个条件,再增加另一个条件;
A
B
C
10
6
用“AC=8”换掉“AB=10,BC=6”中的任何一个条件均可.
(2)改变两条边长,即“AB=10,BC=6”两个条件中的数据都改为其他数,有多少种改法,这些不同的改法有什么共同特点?
A
B
C
10
6
有无数种改法,比如:
AB=5,BC=3;
或AB=15,BC=9;
或AB=1,BC=0.6;等等.
这些不同的改法中,AB:BC=5:3.
(3)不给出两条边长的具体数值,可以吗?尝试写出一个符合题意的条件,并进行解答;
A
B
C
把“AB=10,BC=6”改为“AB:BC=5:3”.
解:设AB=5k,则BC=3k,
由勾股定理,得
因此
(4)只给出∠B的一个三角函数值,没有关于边长的条件,可以吗?尝试编题并解答.
A
B
C
例:在 Rt△ABC 中,∠C=90°, 求sinA,cosA,tanA的值
由勾股定理,得
因此
解:由 得,若设AB=5k,则BC=3k,
3.给出∠B的一个三角函数值,以及“AB=10,BC=6”中的一个条件,能求出什么?尝试编题并解答.
能求其他未知的边长和锐角三角函数值.
A
B
C
10
6
例:在 Rt△ABC 中,∠C=90°,BC=6,
求AC,AB以及sinA,cosA,tanA,sinB,tanB的值.
由勾股定理,得
解:由 得,若设AB=5k,则BC=3k,
A
B
C
6
由BC=6,得3k=6,解得k=2,则AB=10.
因此
对比上述两个锐角的三角函数值,发现什么等量关系?为什么会有这种关系?
sinA=cosB,cosA=sinB,tanA·tanB=1.
由锐角的正弦、余弦和正切定义,可知:
A
B
C
1. 教材第65页练习第1-2题.
2. 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若 BC=4,AB=5,则
sinA=______,cosB=______,tanA=______.
·
A
O
B
C
课堂练习
4. 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,
若 ,
那么 ( )
B
a
O
C
D
B
A
P
3. 如图,在 Rt△ABC 中,斜边 AB 的长为 m,∠A=35°,则直角边 BC 的长是 ( )
A.
B.
C.
D.
A
A
B
C
5. 如图,在 Rt△ABC 中,∠C = 90°,cosA = ,求 sinA,tanA 的值.
解:
A
B
C
设 AC = 15k,则 AB = 17k.
由勾股定理,得
∴
课堂小结
1.综合两节课所学内容,说一下常见的三种锐角三角函数的求法.
2.为什么说锐角三角函数是一种函数,谁是谁的函数?谁是自变量?
3.结合本节课所学内容,谈一下你对类比思想的认识.
正弦
余弦
正切
锐角∠A的
三角函数
布置作业
A组:
1.教材第68页习题28.1第1题(只求余弦值和正切值),第2题.
2.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
B组:
1.教材第70页习题28.1第10题(证明结论).
2. 如图,在△ABC中,AB=AC=4,BC=6. 求cosB,tanC的值.
A
B
C
提示:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.
