初中数学人教版九下28.1 锐角三角函数(第3课时) 课件(共20张PPT)
文档属性
| 名称 | 初中数学人教版九下28.1 锐角三角函数(第3课时) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 291.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 08:33:26 | ||
图片预览




文档简介
(共20张PPT)
28.1 锐角三角函数
(第3课时)
第二十八章 锐角三角函数
学习目标
1.掌握30°,45°,60°角的正弦、余弦和正切值.(重点)
2.会使用计算器进行锐角三角函数的相关计算.(难点)
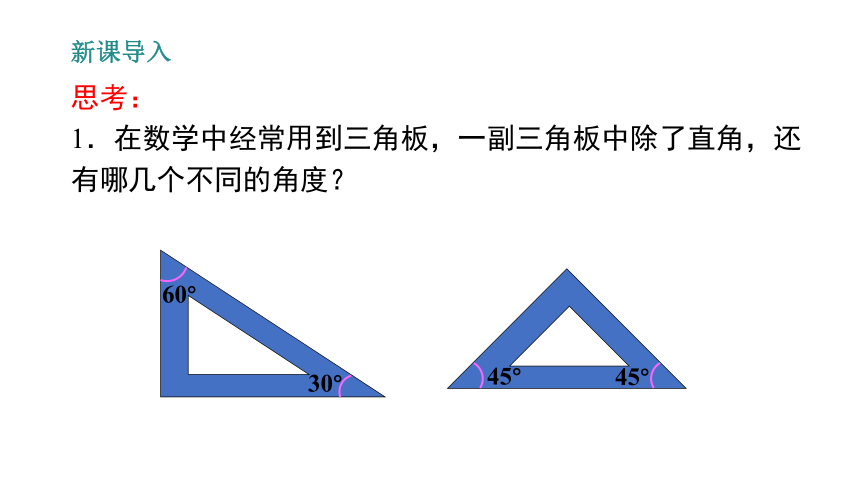
思考:
1.在数学中经常用到三角板,一副三角板中除了直角,还有哪几个不同的角度?
新课导入
30°
60°
45°
45°
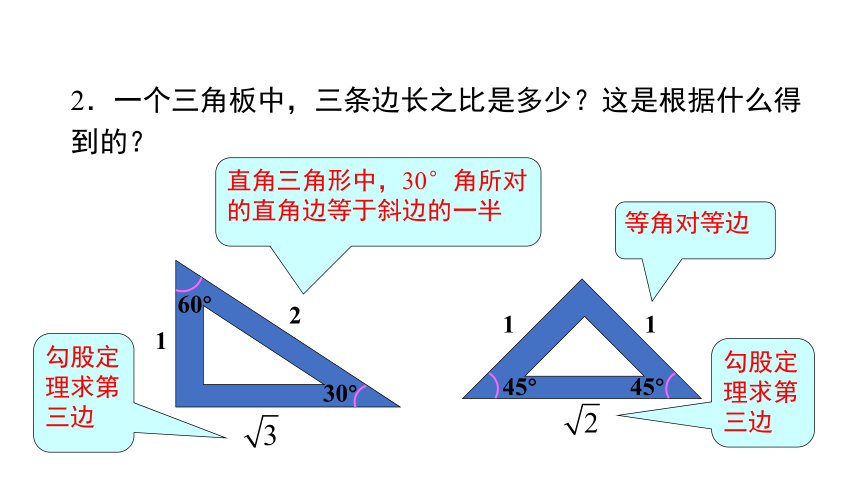
2.一个三角板中,三条边长之比是多少?这是根据什么得到的?
30°
60°
45°
45°
1
2
1
1
直角三角形中,30°角所对的直角边等于斜边的一半
勾股定理求第三边
勾股定理求第三边
等角对等边
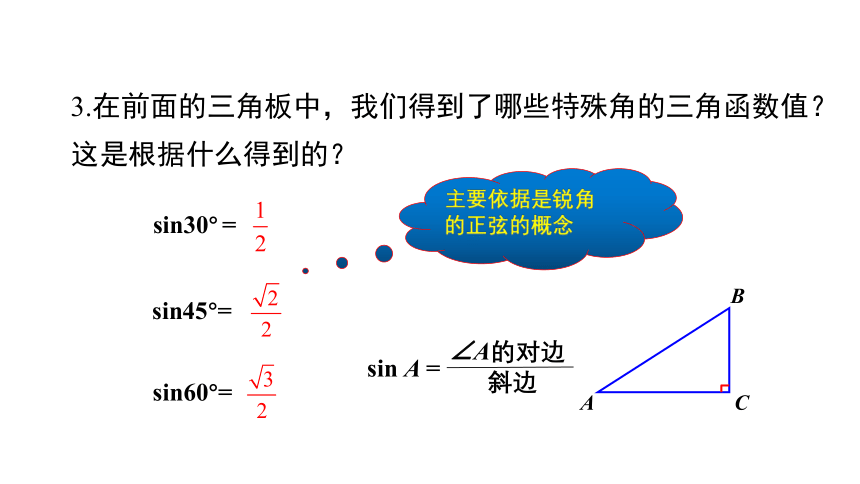
3.在前面的三角板中,我们得到了哪些特殊角的三角函数值?这是根据什么得到的?
sin45°=
sin30° =
sin60°=
主要依据是锐角的正弦的概念
∠A的对边
斜边
sin A =
A
B
C
讲授新课
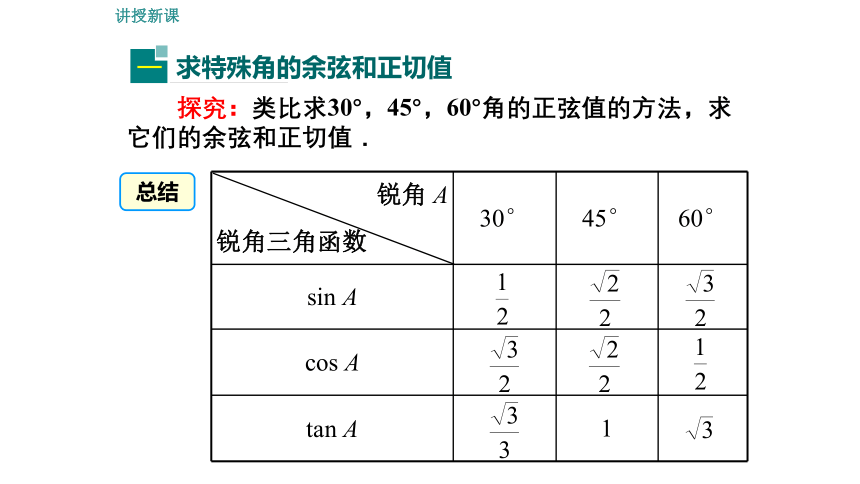
求特殊角的余弦和正切值
一
锐角 A 锐角三角函数 30° 45° 60°
sin A
cos A
tan A
探究:类比求30°,45°,60°角的正弦值的方法,求它们的余弦和正切值.
1
总结
例3 求下列各式的值:
解:cos260°+sin260°
(1) cos260°+sin260°;
(2)
解:
利用特殊角的三角函数值解题
二
cos260°表示(cos60°)2,即 (cos60°) (cos60°).
求含有特殊角三角函数的算式的值,
先把三角函数的值代入算式,
再进行计算.
归纳总结
A
B
C
图1
图2
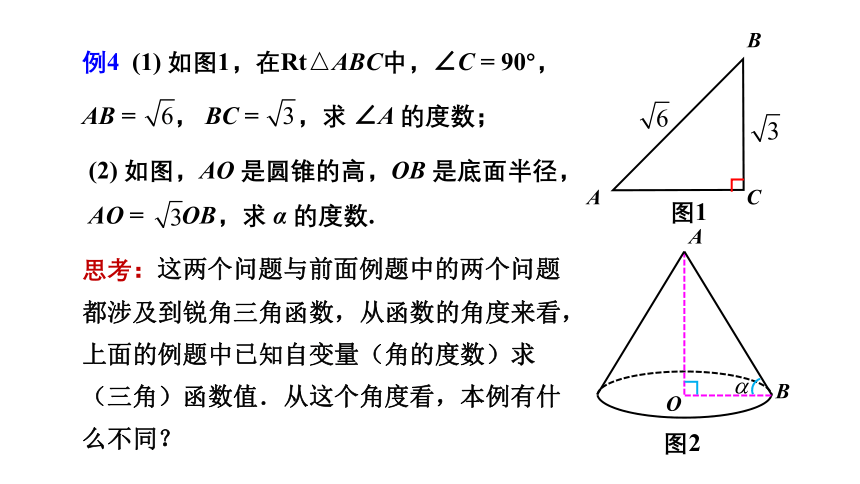
例4 (1) 如图1,在Rt△ABC中,∠C = 90°,
AB = , BC = ,求 ∠A 的度数;
(2) 如图,AO 是圆锥的高,OB 是底面半径,
AO = OB,求 α 的度数.
A
B
O
思考:这两个问题与前面例题中的两个问题都涉及到锐角三角函数,从函数的角度来看,上面的例题中已知自变量(角的度数)求(三角)函数值.从这个角度看,本例有什么不同?
解: 在图中,
A
B
C
例4 (1) 如图1,在Rt△ABC中,∠C = 90°,AB = , BC = ,
求 ∠A 的度数;
∴ ∠A = 45°.
∵
图1
解: 在图2中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图2,AO 是圆锥的高,OB 是底面半径,AO = OB,求 α 的度数.
图2
像其他函数一样,三角函数既可以已知自变量求函数值,也可以由函数值求自变量.
归纳
自变量
(锐角的度数)
函数值
(三角函数值)
用计算器求锐角三角函数值
三
问题:除了特殊角的三角函数值外,一般锐角的三角函数值怎样求得呢?
阅读:学生阅读教材第67-68页两个“练习”之间的内容,或者阅读科学计算器中关于锐角三角函数的使用说明.
操作:一边阅读文本,一边操作计算器,不明白的地方可以讨论解决.
用计算器求锐角的三角函数,操作步骤如下:
第一步:按计算器上的三角函数名称键;
第二步:输入角度值(可使用 键);
第三步:屏幕显示三角函数值.
归纳总结
° ′ ″
根据三角函数值用计算器求锐角,操作步骤如下:
第一步:先后按计算器上的 和三角函数名称键;
第二步:输入三角函数值;
第三步:屏幕显示锐角度数(可使用 和
键,把结果单位改为度分秒).
归纳总结
2nd F
° ′ ″
2nd F
3. 在Rt△ABC中,∠C=90°, ,求∠A,∠B的度数.
B
A
C
解: 由勾股定理,得
∴ ∠ A=30°,∠B = 90°- ∠ A = 90°-30°= 60°.
1.教材第67页练习第1-2题.(配套“活动二”完成)
2.教材第68页练习第1-2题.(配套“活动三”完成)
课堂练习
4. 在 Rt△ABC 中,∠C = 90°,∠BAC = 42°24′,∠BAC 的平分线 AT = 14.7 cm,用计算器求 AC 的长(精确到0.001cm).
解:∵ AT 平分∠BAC,且∠BAC = 42°24′,
∴ ∠CAT = ∠BAC = 21°12′.
在 Rt△ACT 中 ,cos∠CAT = ,
∴ AC = AT · cos∠CAT = 14.7×cos21°12′ ≈13.705(cm).
课堂小结
1.本节课学习了哪些知识?
2.用这些知识能够解决哪些数学问题?
3.从“函数思想”和“数形结合思想”的角度,谈谈自己有什么收获?
30°,45°,60°角的三角函数值
三角函数
的概念
用计算器解锐角三角函数问题
自变量
(锐角的度数)
函数值
(三角函数值)
布置作业
A组:教材第69页习题28.1第3-5题.
B组:教材第69页习题28.1第7-9题.
28.1 锐角三角函数
(第3课时)
第二十八章 锐角三角函数
学习目标
1.掌握30°,45°,60°角的正弦、余弦和正切值.(重点)
2.会使用计算器进行锐角三角函数的相关计算.(难点)
思考:
1.在数学中经常用到三角板,一副三角板中除了直角,还有哪几个不同的角度?
新课导入
30°
60°
45°
45°
2.一个三角板中,三条边长之比是多少?这是根据什么得到的?
30°
60°
45°
45°
1
2
1
1
直角三角形中,30°角所对的直角边等于斜边的一半
勾股定理求第三边
勾股定理求第三边
等角对等边
3.在前面的三角板中,我们得到了哪些特殊角的三角函数值?这是根据什么得到的?
sin45°=
sin30° =
sin60°=
主要依据是锐角的正弦的概念
∠A的对边
斜边
sin A =
A
B
C
讲授新课
求特殊角的余弦和正切值
一
锐角 A 锐角三角函数 30° 45° 60°
sin A
cos A
tan A
探究:类比求30°,45°,60°角的正弦值的方法,求它们的余弦和正切值.
1
总结
例3 求下列各式的值:
解:cos260°+sin260°
(1) cos260°+sin260°;
(2)
解:
利用特殊角的三角函数值解题
二
cos260°表示(cos60°)2,即 (cos60°) (cos60°).
求含有特殊角三角函数的算式的值,
先把三角函数的值代入算式,
再进行计算.
归纳总结
A
B
C
图1
图2
例4 (1) 如图1,在Rt△ABC中,∠C = 90°,
AB = , BC = ,求 ∠A 的度数;
(2) 如图,AO 是圆锥的高,OB 是底面半径,
AO = OB,求 α 的度数.
A
B
O
思考:这两个问题与前面例题中的两个问题都涉及到锐角三角函数,从函数的角度来看,上面的例题中已知自变量(角的度数)求(三角)函数值.从这个角度看,本例有什么不同?
解: 在图中,
A
B
C
例4 (1) 如图1,在Rt△ABC中,∠C = 90°,AB = , BC = ,
求 ∠A 的度数;
∴ ∠A = 45°.
∵
图1
解: 在图2中,
A
B
O
∴ α = 60°.
∵ tanα = ,
(2) 如图2,AO 是圆锥的高,OB 是底面半径,AO = OB,求 α 的度数.
图2
像其他函数一样,三角函数既可以已知自变量求函数值,也可以由函数值求自变量.
归纳
自变量
(锐角的度数)
函数值
(三角函数值)
用计算器求锐角三角函数值
三
问题:除了特殊角的三角函数值外,一般锐角的三角函数值怎样求得呢?
阅读:学生阅读教材第67-68页两个“练习”之间的内容,或者阅读科学计算器中关于锐角三角函数的使用说明.
操作:一边阅读文本,一边操作计算器,不明白的地方可以讨论解决.
用计算器求锐角的三角函数,操作步骤如下:
第一步:按计算器上的三角函数名称键;
第二步:输入角度值(可使用 键);
第三步:屏幕显示三角函数值.
归纳总结
° ′ ″
根据三角函数值用计算器求锐角,操作步骤如下:
第一步:先后按计算器上的 和三角函数名称键;
第二步:输入三角函数值;
第三步:屏幕显示锐角度数(可使用 和
键,把结果单位改为度分秒).
归纳总结
2nd F
° ′ ″
2nd F
3. 在Rt△ABC中,∠C=90°, ,求∠A,∠B的度数.
B
A
C
解: 由勾股定理,得
∴ ∠ A=30°,∠B = 90°- ∠ A = 90°-30°= 60°.
1.教材第67页练习第1-2题.(配套“活动二”完成)
2.教材第68页练习第1-2题.(配套“活动三”完成)
课堂练习
4. 在 Rt△ABC 中,∠C = 90°,∠BAC = 42°24′,∠BAC 的平分线 AT = 14.7 cm,用计算器求 AC 的长(精确到0.001cm).
解:∵ AT 平分∠BAC,且∠BAC = 42°24′,
∴ ∠CAT = ∠BAC = 21°12′.
在 Rt△ACT 中 ,cos∠CAT = ,
∴ AC = AT · cos∠CAT = 14.7×cos21°12′ ≈13.705(cm).
课堂小结
1.本节课学习了哪些知识?
2.用这些知识能够解决哪些数学问题?
3.从“函数思想”和“数形结合思想”的角度,谈谈自己有什么收获?
30°,45°,60°角的三角函数值
三角函数
的概念
用计算器解锐角三角函数问题
自变量
(锐角的度数)
函数值
(三角函数值)
布置作业
A组:教材第69页习题28.1第3-5题.
B组:教材第69页习题28.1第7-9题.
