苏教版八年级数学上册试题 6.1函数同步练习(含答案)
文档属性
| 名称 | 苏教版八年级数学上册试题 6.1函数同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 78.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 10:35:09 | ||
图片预览



文档简介
6.1函数
一、选择题
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A.1个 B.2个 C.3个 D.4个
3.某人要在规定的时间内加工100个零件,如果用n表示工作效率,用t表示规定的时间,下列说法正确的是( )
A.数100和n,t都是常量 B.数100和n都是变量
C.n和t都是变量 D.数100和t都是变量
4.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
5.将温度计从热茶的杯子中取出之后,立即被放入一杯凉水中.每隔5s后读一次温度计上显示的度数,将记录下的数据制成下表.下述说法不正确的是( )
时间t(单位:s) 5 10 15 20 25 30
温度计读数(单位:℃) 49.0 31.0 22.0 16.5 14.0 12.0
A.自变量是时间,因变量是温度计的读数
B.当t=10s时,温度计上的读数是31.0℃
C.温度计的读数随着时间推移逐渐减小,最后保持不变
D.依据表格中反映出的规律,t=35s时,温度计上的读数是13.0℃
6.已知弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如表关系,则( )
x(kg) 0 1 2 3 4 5
y(cm) 6 6.5 7 7.5 8 8
A.y随x的增大而增大
B.质量每增加1kg,长度增加0.5cm
C.不挂物体时,长度为6cm
D.质量为6kg时,长度为8.5cm
7.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13 B.5 C.2 D.3.5
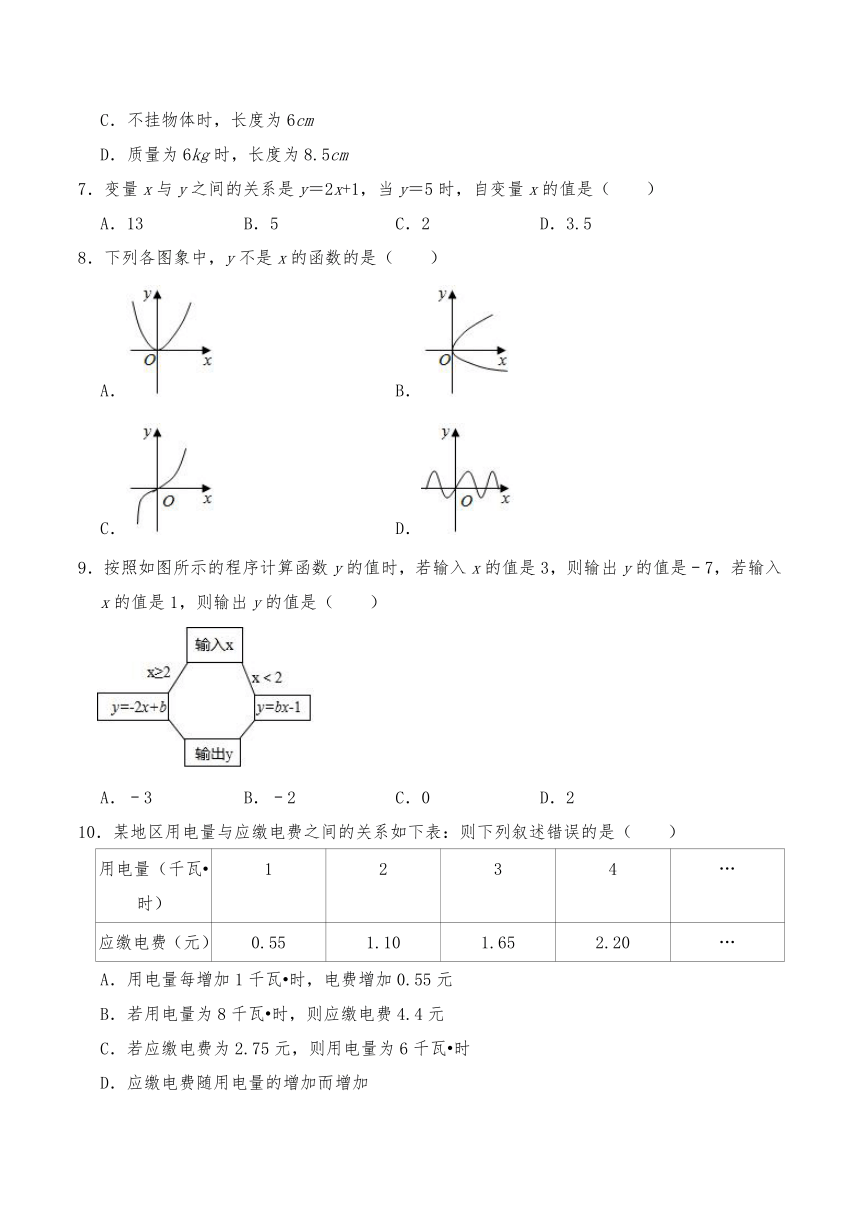
8.下列各图象中,y不是x的函数的是( )
A. B.
C. D.
9.按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
10.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦 时,电费增加0.55元
B.若用电量为8千瓦 时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦 时
D.应缴电费随用电量的增加而增加
二、填空题
11.每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 是常量, 是变量.
12.自变量x与因变量y的关系如图,当x每增加1时,y增加 .
13.小邢到单位附近的加油站加油,下图所示是他所用的加油机上的数据显示牌,则数据中的变量是 .
14.我们知道,地面有一定的温度,高空也有一定的温度,且高空中的温度是随着距地面高度的变化而变化的,如果t表示某高空中的温度,h表示距地面的高度,则 是自变量.
15.声音在空气中传播的速度y(m/s)(简称声速)与气温x(℃)的关系如下表所示:
气温x/℃ 0 5 10 15 20 …
声速y/(m/s) 331 334 337 340 343 …
照此规律可以发现,当气温x为 ℃时,声速y达到352m/s.
16.农村“雨污分流”工程是“美丽乡村”战略的重要组成部分,我县某村要铺设一条全长为1000米的“雨污分流”管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 米.
时间(x天) 1 2 3 4 5 …
管道长度(y米) 20 40 60 80 100 …
17.新型冠状病毒疫情复工、复产后,某商场为了刺激消费,实施薄利多销,减少库存,现将一商品在保持销售价60元/件不变的前提下,规定凡购买超过5件者,超出的部分打6折出售.若顾客购买x(x>5)件,应付y元,则y与x之间的函数关系式是 .
18.某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是 .
年份 第一年 第二年 第三年 第四年 第五年
分枝数 1 1 2 3 5
三、解答题
19.指出下列变化过程中,哪个变量随着另一个变量的变化而变化?
(1)一辆汽车以80km/h的速度匀速行驶,行驶的路程s(km)与行驶时间t(h)
(2)圆的半径r和圆面积S满足:S=πr2.
(3)银行的存款利率P与存期t.
20.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg 0 1 2 3 4 5
弹簧的长度y/cm 20 22 24 26 28 30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是 .不挂重物时,弹簧长是 .
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是 .
21.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
22.有一个容积为350L的水池,现用10台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时可抽水10L.
(1)抽水1小时后,池中还有水 ;
(2)在这一变化过程中哪些是变量,哪些是常量?
(3)几小时后才能把满池水抽干?
23.(巴州区期末)已知一个圆柱的底面半径是3cm,当圆柱的高h(cm)变化时,圆柱的体积V(cm3)也随之变化.
(1)在这个变化过程中,自变量是 ,因变量是 .
(2)在这个变化过程中,写出圆柱的体积V与高h之间的关系式;
(3)当h由3cm变化到6cm时,V是怎样变化的?
24.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁是的2倍、3倍.
(1)上述的那些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
答案
一、选择题
B.C.C.C.D.C.C.B.B.C.
二、填空题
11.电影票的售价;电影票的张数,票房收入.
12.2.
13.金额和数量
14.h.
15.35.
16.840.
17.y=36x+120(x>5).
18.8,年份,分枝数.
三、解答题
19.(1)s=80t,s随着t的变化而变化;
(2)圆的半径r和圆面积S关系式S=πr2,其中S随着r的变化而变化;
(3)银行的存款利率P随着存期t的变化而变化.
20.(1)反映了弹簧长度y与所挂物体质量x之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量;
(2)①根据表格可知:当所挂物体重量为3千克时,弹簧长度为26cm;不挂重物时,弹簧长度为10cm;
故答案为:26cm 20cm.
②根据表格可知:所挂重物每增加1千克,弹簧增长2cm,根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时,弹簧长度y=2x+20,将x=8代入得y=2×8+20=36.
故答案为:36cm.
21.(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
22.(1)抽水1小时后,池中还有水:350﹣10×10=250L;
故答案为:250L;
(2)在这一变化过程中时间、抽水机是常量,池中的水是变量;
(3)根据题意得:
350÷(10×10)=3.5(小时),
答:3.5小时后才能把满池水抽干.
23.(1)在这个变化过程中,自变量是h,因变量是V;
故答案为h,V;
(2)V=π 32 h=9πh;
(3)当h=3cm时,V=27πcm3;当h=6cm时,V=54πcm3;
所以当h由3cm变化到6cm时,V是由27πcm3变化到54πcm3.
24.(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
一、选择题
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A.1个 B.2个 C.3个 D.4个
3.某人要在规定的时间内加工100个零件,如果用n表示工作效率,用t表示规定的时间,下列说法正确的是( )
A.数100和n,t都是常量 B.数100和n都是变量
C.n和t都是变量 D.数100和t都是变量
4.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
5.将温度计从热茶的杯子中取出之后,立即被放入一杯凉水中.每隔5s后读一次温度计上显示的度数,将记录下的数据制成下表.下述说法不正确的是( )
时间t(单位:s) 5 10 15 20 25 30
温度计读数(单位:℃) 49.0 31.0 22.0 16.5 14.0 12.0
A.自变量是时间,因变量是温度计的读数
B.当t=10s时,温度计上的读数是31.0℃
C.温度计的读数随着时间推移逐渐减小,最后保持不变
D.依据表格中反映出的规律,t=35s时,温度计上的读数是13.0℃
6.已知弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如表关系,则( )
x(kg) 0 1 2 3 4 5
y(cm) 6 6.5 7 7.5 8 8
A.y随x的增大而增大
B.质量每增加1kg,长度增加0.5cm
C.不挂物体时,长度为6cm
D.质量为6kg时,长度为8.5cm
7.变量x与y之间的关系是y=2x+1,当y=5时,自变量x的值是( )
A.13 B.5 C.2 D.3.5
8.下列各图象中,y不是x的函数的是( )
A. B.
C. D.
9.按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
10.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦 时,电费增加0.55元
B.若用电量为8千瓦 时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦 时
D.应缴电费随用电量的增加而增加
二、填空题
11.每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 是常量, 是变量.
12.自变量x与因变量y的关系如图,当x每增加1时,y增加 .
13.小邢到单位附近的加油站加油,下图所示是他所用的加油机上的数据显示牌,则数据中的变量是 .
14.我们知道,地面有一定的温度,高空也有一定的温度,且高空中的温度是随着距地面高度的变化而变化的,如果t表示某高空中的温度,h表示距地面的高度,则 是自变量.
15.声音在空气中传播的速度y(m/s)(简称声速)与气温x(℃)的关系如下表所示:
气温x/℃ 0 5 10 15 20 …
声速y/(m/s) 331 334 337 340 343 …
照此规律可以发现,当气温x为 ℃时,声速y达到352m/s.
16.农村“雨污分流”工程是“美丽乡村”战略的重要组成部分,我县某村要铺设一条全长为1000米的“雨污分流”管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 米.
时间(x天) 1 2 3 4 5 …
管道长度(y米) 20 40 60 80 100 …
17.新型冠状病毒疫情复工、复产后,某商场为了刺激消费,实施薄利多销,减少库存,现将一商品在保持销售价60元/件不变的前提下,规定凡购买超过5件者,超出的部分打6折出售.若顾客购买x(x>5)件,应付y元,则y与x之间的函数关系式是 .
18.某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是 .
年份 第一年 第二年 第三年 第四年 第五年
分枝数 1 1 2 3 5
三、解答题
19.指出下列变化过程中,哪个变量随着另一个变量的变化而变化?
(1)一辆汽车以80km/h的速度匀速行驶,行驶的路程s(km)与行驶时间t(h)
(2)圆的半径r和圆面积S满足:S=πr2.
(3)银行的存款利率P与存期t.
20.在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg 0 1 2 3 4 5
弹簧的长度y/cm 20 22 24 26 28 30
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是 .不挂重物时,弹簧长是 .
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是 .
21.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
22.有一个容积为350L的水池,现用10台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时可抽水10L.
(1)抽水1小时后,池中还有水 ;
(2)在这一变化过程中哪些是变量,哪些是常量?
(3)几小时后才能把满池水抽干?
23.(巴州区期末)已知一个圆柱的底面半径是3cm,当圆柱的高h(cm)变化时,圆柱的体积V(cm3)也随之变化.
(1)在这个变化过程中,自变量是 ,因变量是 .
(2)在这个变化过程中,写出圆柱的体积V与高h之间的关系式;
(3)当h由3cm变化到6cm时,V是怎样变化的?
24.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁是的2倍、3倍.
(1)上述的那些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
答案
一、选择题
B.C.C.C.D.C.C.B.B.C.
二、填空题
11.电影票的售价;电影票的张数,票房收入.
12.2.
13.金额和数量
14.h.
15.35.
16.840.
17.y=36x+120(x>5).
18.8,年份,分枝数.
三、解答题
19.(1)s=80t,s随着t的变化而变化;
(2)圆的半径r和圆面积S关系式S=πr2,其中S随着r的变化而变化;
(3)银行的存款利率P随着存期t的变化而变化.
20.(1)反映了弹簧长度y与所挂物体质量x之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量;
(2)①根据表格可知:当所挂物体重量为3千克时,弹簧长度为26cm;不挂重物时,弹簧长度为10cm;
故答案为:26cm 20cm.
②根据表格可知:所挂重物每增加1千克,弹簧增长2cm,根据弹簧的长度=弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时,弹簧长度y=2x+20,将x=8代入得y=2×8+20=36.
故答案为:36cm.
21.(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
22.(1)抽水1小时后,池中还有水:350﹣10×10=250L;
故答案为:250L;
(2)在这一变化过程中时间、抽水机是常量,池中的水是变量;
(3)根据题意得:
350÷(10×10)=3.5(小时),
答:3.5小时后才能把满池水抽干.
23.(1)在这个变化过程中,自变量是h,因变量是V;
故答案为h,V;
(2)V=π 32 h=9πh;
(3)当h=3cm时,V=27πcm3;当h=6cm时,V=54πcm3;
所以当h由3cm变化到6cm时,V是由27πcm3变化到54πcm3.
24.(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
