苏科版八年级数学上册试题 6.3.1函数的图象同步练习(含答案)
文档属性
| 名称 | 苏科版八年级数学上册试题 6.3.1函数的图象同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览


文档简介
6.3.1函数的图象
一、选择题
1.请找出符合以下情景的图象:小颖将一个球被竖直向上抛起,球升到最高点后垂直下落,直到地面,在此过程中,球的速度与时间的关系的图象( )
A. B. C. D.
2.如图,下面图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间之间的关系,下列说法中错误的是( )
A.第3分钟时汽车的速度是40千米/小时
B.第12分钟时汽车的速度是0千米/小时
C.从第3分钟后到第6分钟,汽车停止不动
D.从第9分钟到第12分钟,汽车速度从60千米/小时减少到0千米/小时
3.已知小林的家、体育场、文具店在同一直线上,图中的信息反映的过程:小林从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中x表示时间,y表示小林离家的距离,依据图中的信息,下列说法错误的是( )
A.体育场离小林家2.5 km
B.小林在文具店买笔停留了20min
C.小林从体育场出发到文具店的平均速度是50 m/min
D.小林从文具店回家的平均速度是60 m/min
4.如图所示的函数图象反映的过程是:小明从家去书店选购学习资料,又到体育馆去锻炼身体,然后回家.其中x表示时间,y表示小明离他家的距离.下列结论中:①体育馆离小明家的距离是2千米;②小明从家里到书店的平均速度与从书店到体育馆的平均速度相等;③小明在体育馆锻炼身体的时间是18分; ④小明从体育馆返回家的平均速度是0.08千米/小时.正确的结论有( )
A.①② B.②④ C.①③ D.①③④
5.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度h(cm) 10 20 30 40 50 60 70 80 90 100
小车下滑的时间t(s) 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
下列说法正确的是( )
A.当h=70cm时,t=1.50s
B.h每增加10cm,t减小1.23
C.随着h逐渐变大,t也逐渐变大
D.随着h逐渐升高,小车下滑的平均速度逐渐加快
6.在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(100℃),王红家只有刻度不超过100℃的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔10s测量一次锅中油温,测量得到的数据如下表:
时间t/s 0 10 20 30 40
油温y/℃ 10 30 50 70 90
王红发现,烧了110s时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃
B.加热50s,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃
D.每加热10s,油的温度升高30℃
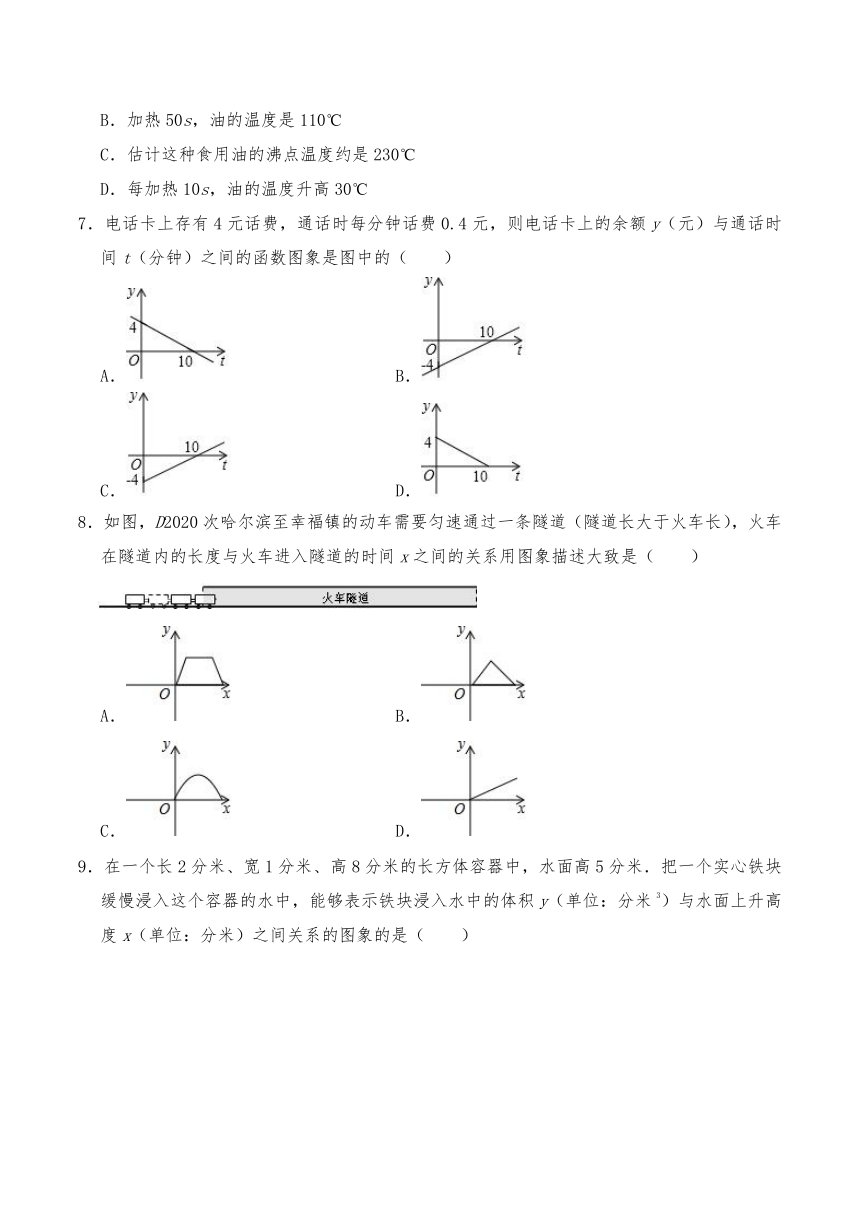
7.电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
8.如图,D2020次哈尔滨至幸福镇的动车需要匀速通过一条隧道(隧道长大于火车长),火车在隧道内的长度与火车进入隧道的时间x之间的关系用图象描述大致是( )
A. B.
C. D.
9.在一个长2分米、宽1分米、高8分米的长方体容器中,水面高5分米.把一个实心铁块缓慢浸入这个容器的水中,能够表示铁块浸入水中的体积y(单位:分米3)与水面上升高度x(单位:分米)之间关系的图象的是( )
A. B.
C. D.
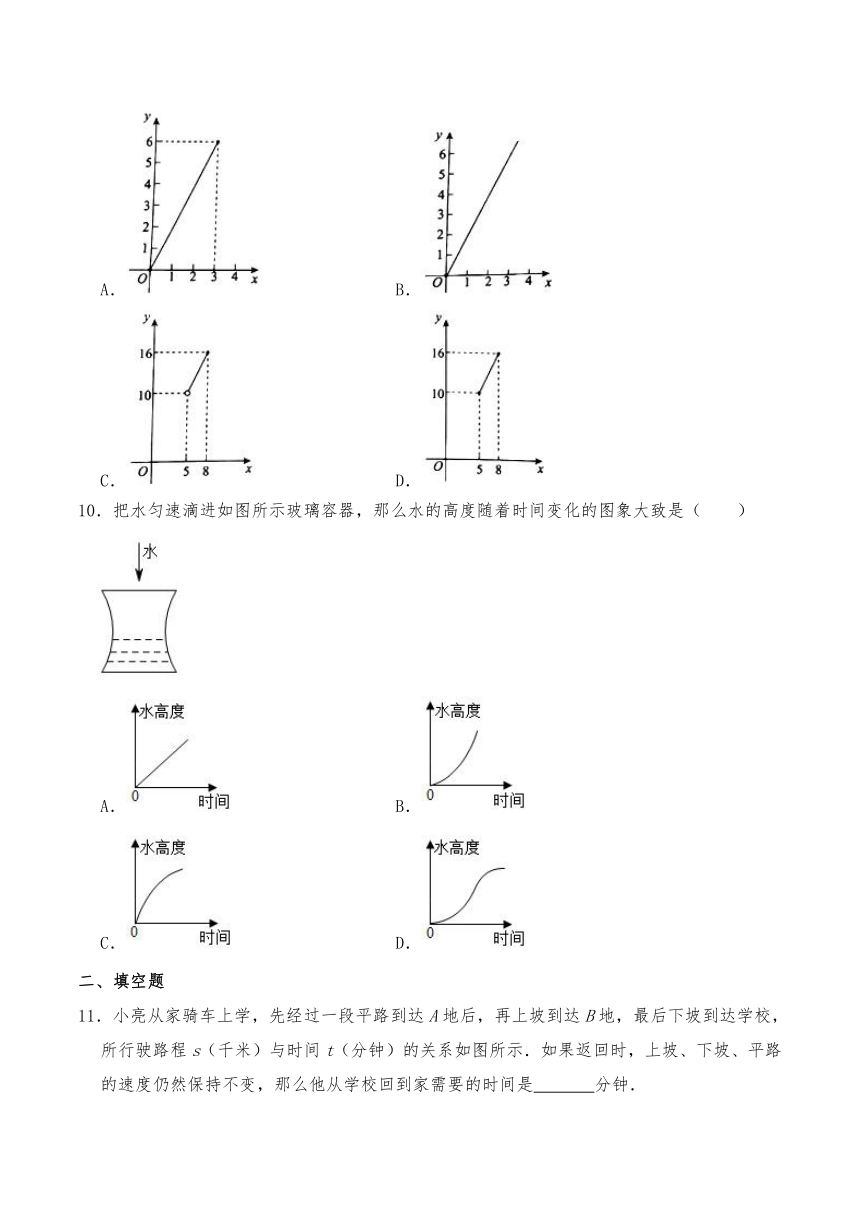
10.把水匀速滴进如图所示玻璃容器,那么水的高度随着时间变化的图象大致是( )
A. B.
C. D.
二、填空题
11.小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间t(分钟)的关系如图所示.如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是 分钟.
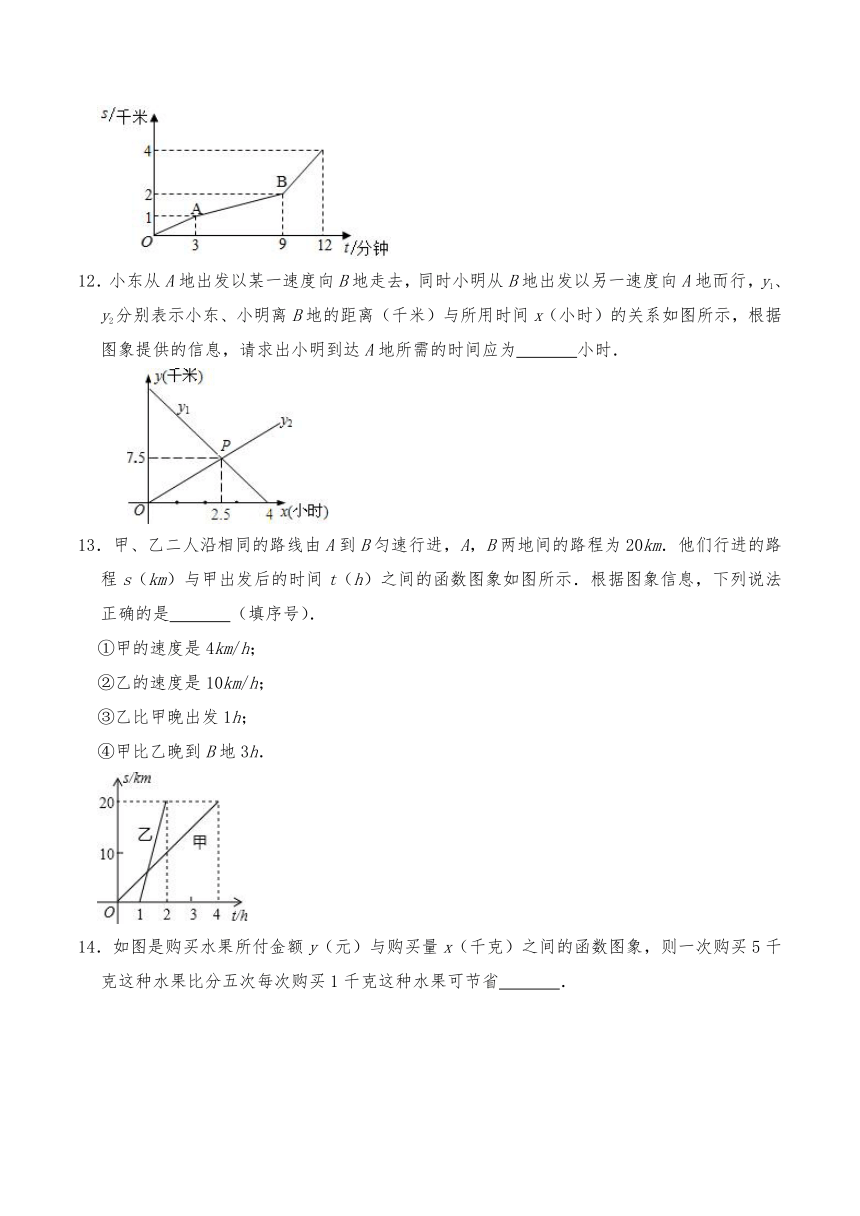
12.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,y1、y2分别表示小东、小明离B地的距离(千米)与所用时间x(小时)的关系如图所示,根据图象提供的信息,请求出小明到达A地所需的时间应为 小时.
13.甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图象信息,下列说法正确的是 (填序号).
①甲的速度是4km/h;
②乙的速度是10km/h;
③乙比甲晚出发1h;
④甲比乙晚到B地3h.
14.如图是购买水果所付金额y(元)与购买量x(千克)之间的函数图象,则一次购买5千克这种水果比分五次每次购买1千克这种水果可节省 .
15.如图,A、B两地相距180km,一列火车从B地出发沿BC方向以120km/h的速度行驶,在行驶过程中,这列火车离A地的路程y(km)与行驶时间x(h)之间的函数关系式是 .
16.某计算程序编辑如图所示,当输入x= 时,输出的y=3.
17.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 .
18.经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是 (填入序号即可).
三、解答题
19.如图所示是鞍山市的某一天的气温变化图,在这一天中,气温随着时间的变化而变化.请观察图象,回答下列问题:
(1)在这一天中(凌晨0时到深夜24时均在内)气温在什么时候达到最高,最高温度为多少摄氏度?
(2)什么时间气温达到最低,最低气温是多少摄氏度?
(3)上午10时、下午20时的气温各为多少摄氏度?
(4)如果某旅行团这天想去登山,登山的气温最好在18℃以上,请问该旅行团适宜登山的时间从几点开始?共有多长时间适宜登山?
20.新冠病毒防疫期间,草莓摊主小钱为避免交叉感染的风险,建议顾客选择微信支付,尽量不使用现金,早上开始营业前,他查看了自己的微信零钱;销售完20kg后,他又一次查看了微信零钱,由于草莓所剩不多,他想早点卖完回家,于是每千克降价10元销售,很快销售一空,小钱弟弟根据小钱的微信零钱(元)与销售草莓数量(kg)之间的关系绘制了下列图象,请你根据以上信息回答下列问题:
(1)图象中A点表示的意义是什么?
(2)降价前草莓每千克售价多少元?
(3)小钱卖完所有草莓微信零钱应有多少元?
21.小明家距离学校8千米,今天早晨,小明骑车上学图中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系.请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明从早晨出发直到到达学校共用了多少分钟?
(3)小明修车前、后的行驶速度分别是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?
22.如图所示,小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)他到达离家最远的地方是什么时间?离家多远?
(3)10时到12时他行驶了多少千米?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
23.小明从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是小明离家的距离与时间的关系图象.根据图象回答下列问题:
(1)体育场离小明家 千米.
(2)小明在文具店逗留了 分钟.
(3)求小明从文具店到家的速度(千米/时)是多少?
24.(竞秀区期末)某地举行龙舟赛,甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(1)最先到达终点的是 队,比另一队领先 分钟到达;
(2)在比赛过程中,甲队的速度始终保持为 米/分;而乙队在第 分钟后第一次加速,速度变为 米/分,在第 分钟后第二次加速;
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
答案
一、选择题
D.C.C.C.D.D.D.A.A.D.
二、填空题
11.16.5.
12..
13.③.
14.6元.
15.y=180+120t(t≥0).
16.12或.
17.y=24﹣3x(0≤x<8).
18.①.
三、解答题
19.由图象可知,
(1)下午14时气温达到最高,最高温度为22℃;
(2)深夜24时气温达到最低,最低温度约为10℃;
(3)上午10时气温20℃,下午20时气温为14℃;
(4)该旅行团适宜登山的时间从上午8时30分开始,共有9.5小时适宜登山.
20.(1)由图象可知,小钱开始营业前微信零钱有50元;
(2)由图象可知,销售草莓20kg后,小钱的微信零钱为650元,
∴销售草莓20kg,销售收入为650﹣50=600元,
∴降价前草莓每千克售价为:600÷20=30(元);
(3)降价后草莓每千克售价为:30﹣10=20元,
∴小钱卖完所有草莓微信零钱为:650+5×20=750(元),
答:小钱卖完所有草莓微信零钱应该有750元.
21.(1)由图可知,小明行了3千米时,自行车出现故障,
修车用了15﹣10=5(分钟);
(2)小明共用了30分钟到学校;
(3)修车前速度:3÷10=0.3千米/分,
修车后速度:5÷15千米/分;
(4)8(分种),
30(分钟),
故他比实际情况早到分钟.
22.(1)图象表示了离家的距离与时间这两个变量之间的关系.其中时间是自变量,离家的距离是因变量;
(2)根据图象可知,他到达离家最远的地方是在12时,离家30千米;
(3)根据图象可知,30﹣15=15(千米).故:10时到12时他行驶了15千米;
(4)根据图象可知,他可能在10时30分到11时或12时到13时间内休息,并吃午餐;
(5)根据图象可知,30÷(15﹣13)=15(千米/时).
故:他由离家最远的地方返回时的平均速度是15千米/时.
23.(1)由图象可知,体育场离小明家2.5千米.
故答案为:2.5;
(2)由图象可知,小明在文具店逗留了:65﹣45=20(分钟).
故答案为:20;
(3)1.5(km/h),
答:小明从文具店到家的速度为千米/时.
24.(1)由函数图象得:
最先到达终点的是乙队,比另一队领先6﹣5=1分钟到达.
故答案为:乙,1;
(2)由函数图象得:
甲的速度为:900÷6=150米/分,而乙队在第2分钟后第一次加速,其速度为(500﹣200)÷2=150米/分,第4分钟后第二次加速.
故答案为:150,2,150,4;
(3)乙队在第一次加速后,始终保持这个速度继续前进走完余下路程需要的时间为
700÷150,
∴乙队走完全程的时间为分钟.
∵甲队行驶完全程需要的时间是6分钟.,
∴甲先到达终点.
一、选择题
1.请找出符合以下情景的图象:小颖将一个球被竖直向上抛起,球升到最高点后垂直下落,直到地面,在此过程中,球的速度与时间的关系的图象( )
A. B. C. D.
2.如图,下面图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间之间的关系,下列说法中错误的是( )
A.第3分钟时汽车的速度是40千米/小时
B.第12分钟时汽车的速度是0千米/小时
C.从第3分钟后到第6分钟,汽车停止不动
D.从第9分钟到第12分钟,汽车速度从60千米/小时减少到0千米/小时
3.已知小林的家、体育场、文具店在同一直线上,图中的信息反映的过程:小林从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中x表示时间,y表示小林离家的距离,依据图中的信息,下列说法错误的是( )
A.体育场离小林家2.5 km
B.小林在文具店买笔停留了20min
C.小林从体育场出发到文具店的平均速度是50 m/min
D.小林从文具店回家的平均速度是60 m/min
4.如图所示的函数图象反映的过程是:小明从家去书店选购学习资料,又到体育馆去锻炼身体,然后回家.其中x表示时间,y表示小明离他家的距离.下列结论中:①体育馆离小明家的距离是2千米;②小明从家里到书店的平均速度与从书店到体育馆的平均速度相等;③小明在体育馆锻炼身体的时间是18分; ④小明从体育馆返回家的平均速度是0.08千米/小时.正确的结论有( )
A.①② B.②④ C.①③ D.①③④
5.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
支撑物的高度h(cm) 10 20 30 40 50 60 70 80 90 100
小车下滑的时间t(s) 4.23 3.00 2.45 2.13 1.89 1.71 1.59 1.50 1.41 1.35
下列说法正确的是( )
A.当h=70cm时,t=1.50s
B.h每增加10cm,t减小1.23
C.随着h逐渐变大,t也逐渐变大
D.随着h逐渐升高,小车下滑的平均速度逐渐加快
6.在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(100℃),王红家只有刻度不超过100℃的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔10s测量一次锅中油温,测量得到的数据如下表:
时间t/s 0 10 20 30 40
油温y/℃ 10 30 50 70 90
王红发现,烧了110s时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃
B.加热50s,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃
D.每加热10s,油的温度升高30℃
7.电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
8.如图,D2020次哈尔滨至幸福镇的动车需要匀速通过一条隧道(隧道长大于火车长),火车在隧道内的长度与火车进入隧道的时间x之间的关系用图象描述大致是( )
A. B.
C. D.
9.在一个长2分米、宽1分米、高8分米的长方体容器中,水面高5分米.把一个实心铁块缓慢浸入这个容器的水中,能够表示铁块浸入水中的体积y(单位:分米3)与水面上升高度x(单位:分米)之间关系的图象的是( )
A. B.
C. D.
10.把水匀速滴进如图所示玻璃容器,那么水的高度随着时间变化的图象大致是( )
A. B.
C. D.
二、填空题
11.小亮从家骑车上学,先经过一段平路到达A地后,再上坡到达B地,最后下坡到达学校,所行驶路程s(千米)与时间t(分钟)的关系如图所示.如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是 分钟.
12.小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,y1、y2分别表示小东、小明离B地的距离(千米)与所用时间x(小时)的关系如图所示,根据图象提供的信息,请求出小明到达A地所需的时间应为 小时.
13.甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示.根据图象信息,下列说法正确的是 (填序号).
①甲的速度是4km/h;
②乙的速度是10km/h;
③乙比甲晚出发1h;
④甲比乙晚到B地3h.
14.如图是购买水果所付金额y(元)与购买量x(千克)之间的函数图象,则一次购买5千克这种水果比分五次每次购买1千克这种水果可节省 .
15.如图,A、B两地相距180km,一列火车从B地出发沿BC方向以120km/h的速度行驶,在行驶过程中,这列火车离A地的路程y(km)与行驶时间x(h)之间的函数关系式是 .
16.某计算程序编辑如图所示,当输入x= 时,输出的y=3.
17.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 .
18.经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线,其中表示客户希望的需求曲线的是 (填入序号即可).
三、解答题
19.如图所示是鞍山市的某一天的气温变化图,在这一天中,气温随着时间的变化而变化.请观察图象,回答下列问题:
(1)在这一天中(凌晨0时到深夜24时均在内)气温在什么时候达到最高,最高温度为多少摄氏度?
(2)什么时间气温达到最低,最低气温是多少摄氏度?
(3)上午10时、下午20时的气温各为多少摄氏度?
(4)如果某旅行团这天想去登山,登山的气温最好在18℃以上,请问该旅行团适宜登山的时间从几点开始?共有多长时间适宜登山?
20.新冠病毒防疫期间,草莓摊主小钱为避免交叉感染的风险,建议顾客选择微信支付,尽量不使用现金,早上开始营业前,他查看了自己的微信零钱;销售完20kg后,他又一次查看了微信零钱,由于草莓所剩不多,他想早点卖完回家,于是每千克降价10元销售,很快销售一空,小钱弟弟根据小钱的微信零钱(元)与销售草莓数量(kg)之间的关系绘制了下列图象,请你根据以上信息回答下列问题:
(1)图象中A点表示的意义是什么?
(2)降价前草莓每千克售价多少元?
(3)小钱卖完所有草莓微信零钱应有多少元?
21.小明家距离学校8千米,今天早晨,小明骑车上学图中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系.请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明从早晨出发直到到达学校共用了多少分钟?
(3)小明修车前、后的行驶速度分别是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?
22.如图所示,小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)他到达离家最远的地方是什么时间?离家多远?
(3)10时到12时他行驶了多少千米?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
23.小明从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是小明离家的距离与时间的关系图象.根据图象回答下列问题:
(1)体育场离小明家 千米.
(2)小明在文具店逗留了 分钟.
(3)求小明从文具店到家的速度(千米/时)是多少?
24.(竞秀区期末)某地举行龙舟赛,甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(1)最先到达终点的是 队,比另一队领先 分钟到达;
(2)在比赛过程中,甲队的速度始终保持为 米/分;而乙队在第 分钟后第一次加速,速度变为 米/分,在第 分钟后第二次加速;
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
答案
一、选择题
D.C.C.C.D.D.D.A.A.D.
二、填空题
11.16.5.
12..
13.③.
14.6元.
15.y=180+120t(t≥0).
16.12或.
17.y=24﹣3x(0≤x<8).
18.①.
三、解答题
19.由图象可知,
(1)下午14时气温达到最高,最高温度为22℃;
(2)深夜24时气温达到最低,最低温度约为10℃;
(3)上午10时气温20℃,下午20时气温为14℃;
(4)该旅行团适宜登山的时间从上午8时30分开始,共有9.5小时适宜登山.
20.(1)由图象可知,小钱开始营业前微信零钱有50元;
(2)由图象可知,销售草莓20kg后,小钱的微信零钱为650元,
∴销售草莓20kg,销售收入为650﹣50=600元,
∴降价前草莓每千克售价为:600÷20=30(元);
(3)降价后草莓每千克售价为:30﹣10=20元,
∴小钱卖完所有草莓微信零钱为:650+5×20=750(元),
答:小钱卖完所有草莓微信零钱应该有750元.
21.(1)由图可知,小明行了3千米时,自行车出现故障,
修车用了15﹣10=5(分钟);
(2)小明共用了30分钟到学校;
(3)修车前速度:3÷10=0.3千米/分,
修车后速度:5÷15千米/分;
(4)8(分种),
30(分钟),
故他比实际情况早到分钟.
22.(1)图象表示了离家的距离与时间这两个变量之间的关系.其中时间是自变量,离家的距离是因变量;
(2)根据图象可知,他到达离家最远的地方是在12时,离家30千米;
(3)根据图象可知,30﹣15=15(千米).故:10时到12时他行驶了15千米;
(4)根据图象可知,他可能在10时30分到11时或12时到13时间内休息,并吃午餐;
(5)根据图象可知,30÷(15﹣13)=15(千米/时).
故:他由离家最远的地方返回时的平均速度是15千米/时.
23.(1)由图象可知,体育场离小明家2.5千米.
故答案为:2.5;
(2)由图象可知,小明在文具店逗留了:65﹣45=20(分钟).
故答案为:20;
(3)1.5(km/h),
答:小明从文具店到家的速度为千米/时.
24.(1)由函数图象得:
最先到达终点的是乙队,比另一队领先6﹣5=1分钟到达.
故答案为:乙,1;
(2)由函数图象得:
甲的速度为:900÷6=150米/分,而乙队在第2分钟后第一次加速,其速度为(500﹣200)÷2=150米/分,第4分钟后第二次加速.
故答案为:150,2,150,4;
(3)乙队在第一次加速后,始终保持这个速度继续前进走完余下路程需要的时间为
700÷150,
∴乙队走完全程的时间为分钟.
∵甲队行驶完全程需要的时间是6分钟.,
∴甲先到达终点.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
