苏科版八年级数学上册试题 6.4用一次函数解决问题--行程问题同步练习(含答案)
文档属性
| 名称 | 苏科版八年级数学上册试题 6.4用一次函数解决问题--行程问题同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 172.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 10:58:47 | ||
图片预览


文档简介
6.4用一次函数解决问题--行程问题
一、选择题.
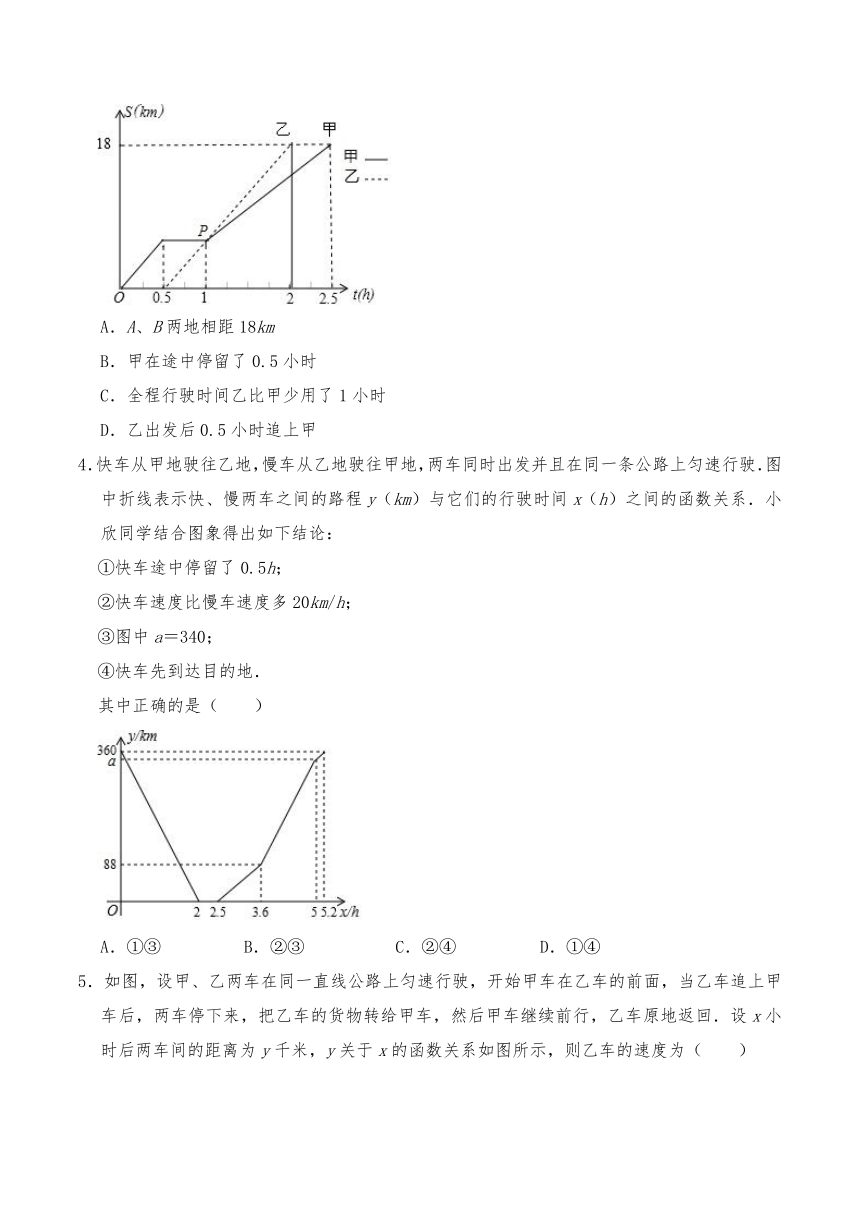
1.A,B两地相距30km,甲乙两人沿同一条路线从A地到B地.如图,反映的是两人行进路程y(km)与行进时间t(h)之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上.以上说法正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.一条笔直的小路上顺次有A,B,C三个道口,甲、乙两人分别从A、B道口同时出发,各自匀速前往C道口,约定先到者在C道口等待,甲、乙两人间的距离y(米)与甲步行的时间x(分钟)之间的关系如图所示,则下列说法中错误的是( )
A.道口A、B相距660米 B.道口B、C相距1440米
C.甲的速度是70米/分 D.乙的速度是64米/分
3.如图,甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离为S(km)和行驶时间t(h)之间的函数关系的图象如图所示,则下列结论错误的是( )
A.A、B两地相距18km
B.甲在途中停留了0.5小时
C.全程行驶时间乙比甲少用了1小时
D.乙出发后0.5小时追上甲
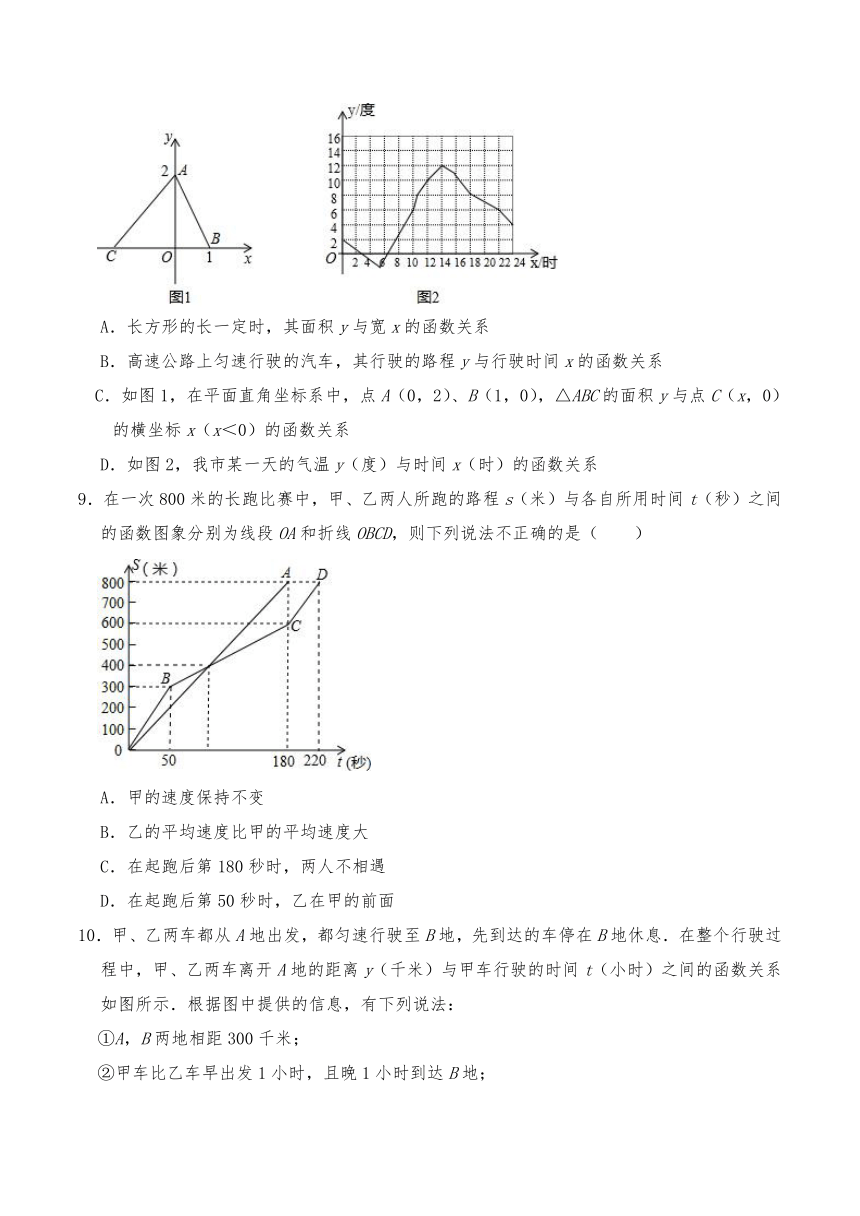
4.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程y(km)与它们的行驶时间x(h)之间的函数关系.小欣同学结合图象得出如下结论:
①快车途中停留了0.5h;
②快车速度比慢车速度多20km/h;
③图中a=340;
④快车先到达目的地.
其中正确的是( )
A.①③ B.②③ C.②④ D.①④
5.如图,设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x小时后两车间的距离为y千米,y关于x的函数关系如图所示,则乙车的速度为( )
A.50千米/小时 B.45千米/小时
C.40千米/小时 D.35千米/小时
6.甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发后步行的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了22.5分钟;
③乙用9分钟追上甲;
④乙到达终点时,甲离终点还有270米.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.一辆货车从甲地匀速驶往乙地用了2.7h,到达后用了0.5h卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的1.5倍,货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示,则a等于( )
A.4.7 B.5.0 C.5.4 D.5.8
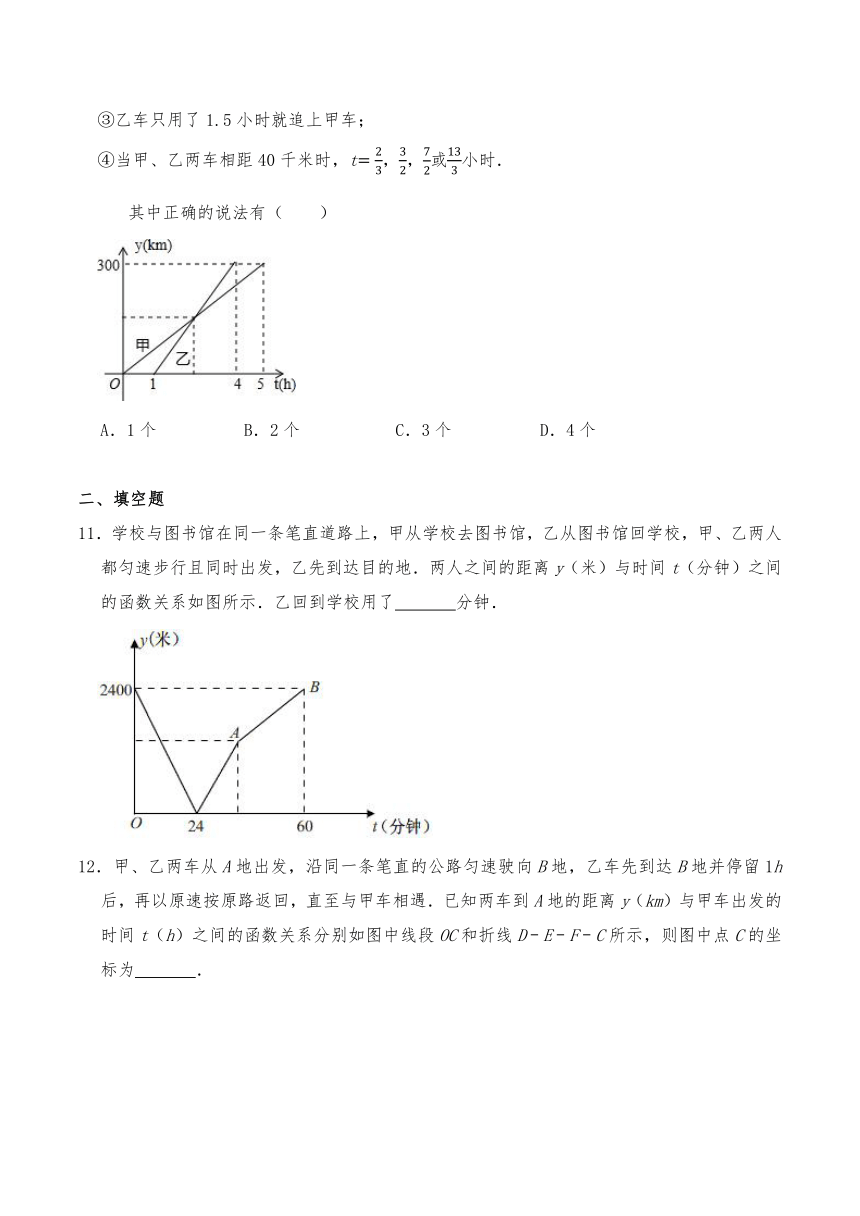
8.下列函数关系中,y随x的增大而减小的是( )
A.长方形的长一定时,其面积y与宽x的函数关系
B.高速公路上匀速行驶的汽车,其行驶的路程y与行驶时间x的函数关系
C.如图1,在平面直角坐标系中,点A(0,2)、B(1,0),△ABC的面积y与点C(x,0)的横坐标x(x<0)的函数关系
D.如图2,我市某一天的气温y(度)与时间x(时)的函数关系
9.在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法不正确的是( )
A.甲的速度保持不变
B.乙的平均速度比甲的平均速度大
C.在起跑后第180秒时,两人不相遇
D.在起跑后第50秒时,乙在甲的前面
10.甲、乙两车都从A地出发,都匀速行驶至B地,先到达的车停在B地休息.在整个行驶过程中,甲、乙两车离开A地的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.根据图中提供的信息,有下列说法:
①A,B两地相距300千米;
②甲车比乙车早出发1小时,且晚1小时到达B地;
③乙车只用了1.5小时就追上甲车;
④当甲、乙两车相距40千米时,t,,或小时.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了 分钟.
12.甲、乙两车从A地出发,沿同一条笔直的公路匀速驶向B地,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.已知两车到A地的距离y(km)与甲车出发的时间t(h)之间的函数关系分别如图中线段OC和折线D﹣E﹣F﹣C所示,则图中点C的坐标为 .
13.如图,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定快者比慢者每秒多跑 米.
14.小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象,则当小帅到达乙地时,小泽距乙地的距离为 千米.
15.小红从家到图书馆查阅资料然后返回,她离家的距离y与离家的时间x之间的对应关系如图所示,如果小红离家50分钟时离家的距离为0.3km,那么她在图书馆查阅资料的时间为 .
16.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B﹣C﹣D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下面几种说法:①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发小时再次与货车相遇;其中正确的是 .(填写序号)
17.一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,到达目的地停车,行驶过程中两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,则快车的速度是 千米/小时.
18.甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.给出下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有 .(把你认为正确结论的序号都填上)
三、解答题
19.某观光湖风景区,一观光轮与一巡逻艇同时从甲码头出发驶往乙码头,巡逻艇匀速往返于甲、乙两个码头之间,当观光轮到达乙码头时,巡逻艇也同时到达乙码头.设出发xh后,观光轮、巡逻艇离甲码头的距离分别为y1km、y2km.图中的线段OG、折线OABCDEFG分别表示y1、y2与x之间的函数关系.
(1)观光轮的速度是 km/h,巡逻艇的速度是 km/h;
(2)求整个过程中观光轮与巡逻艇的最大距离;
(3)求整个过程中观光轮与巡逻艇相遇的最短时间间隔.
20.小丽早晨6:00从家里出发,骑车去菜场买菜,然后从菜场返回家中.小丽离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,请根据图象回答下列问题:
(1)小丽去菜场途中的速度是多少?在菜场逗留了多长时间?
(2)小丽几点几分返回到家?
21.已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时;
(2)求甲、乙两车相遇后y与x之间的函数关系式;
(3)当甲车到达距B地90千米处时,求甲、乙两车之间的路程.
22.甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后.按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为y千米,图中折线OCDE表示接到通知前y与x之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为 千米/小时;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
23.某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(kg)之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题:
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图象中线段BC所在直线对应的函数表达式.
日期 销售记录
6月1日 库存600kg,成本价8元/kg,售价10元/kg(除了促销降价,其他时间售价保持不变).
6月9日 从6月1日至今,一共售出200kg.
6月10、11日 这两天以成本价促销,之后售价恢复到10元/kg.
6月12日 补充进货200kg,成本价8.5元/kg.
6月30日 800kg水果全部售完,一共获利1200元.
24.(张家港市模拟)甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,乙车匀速前往A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(小时),y与x之间的函数图象如图所示.
(1)图中,m= ,n= ;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在甲车返回到A地的过程中,当x为何值时,甲、乙两车相距190千米?
答案
一、选择题.
B.D.C.B.B.D.B.C.B.D.
二、填空题
11.40.
12.(8.4,672).
13.1.5
14.4
15.30分钟.
16.①③.
17.90.
18.①②③.
三、解答题
19.(1)观光轮的速度为:32÷2=16 (km/h),巡逻艇的速度为:(32×7)÷2=112( km/h);
故答案为:16;112;
(2)整个过程中观光轮与巡逻艇的最大距离:32﹣16(km);
(3)由题意可得:16x+112x=32×2,解得x;
,,即点B的坐标为(,0),点C的坐标为(,32),
设线段BC所表示的函数表达式为yBC=kx+b,则,解得,
∴yBC=112x﹣64,
易知y1=16x,
当y1=yBC时,112x﹣64=16x,解得x,.
答:最短时间间隔为 h.
20.(1)3000÷10=300(米/分),
40﹣10=30(分).
答:小丽去菜场途中的速度是300米/分,在菜场逗留了30分钟.
(2)设返回家时,y与x之间的函数关系式为y=kx+b(k≠0),
将(40,3000),(45,2000)代入y=kx+b,得:,
解得:,
∴y与x之间的函数关系式为y=﹣200x+11000.
当y=0时,﹣200x+11000=0,
解得:x=55,
∴小丽6点55分返回到家.
21.(1)由图可得,
乙车的速度为:270÷2﹣60=75(千米/时),
故答案为:75;
(2)a=270÷75=3.6,
故当a=3.6时,两车之间的距离为:60×3.6=216(千米),
b=270÷60=4.5,
当2<x≤3.6时,设y与x之间的函数关系式为y=kx+b,
,
解得,,
即当2<x≤3.6时,y与x之间的函数关系式为y=135x﹣270;
当3.6<x≤4.5时,设y与x之间的函数关系式为y=mx+n,
,
解得,,
即当3.6<x≤4.5时,y与x之间的函数关系式为y=60x;
由上可得,甲、乙两车相遇后,y与x之间的函数关系式为y;
(3)∵甲车到达距B地90千米处时,x3,
∴将x=3代入y=135x﹣270,得
y=135×3﹣270=135,
即当甲车到达距B地90千米处时,甲、乙两车之间的路程是135千米.
22.(1)由图象可知,休息前汽车行驶的速度为80千米/小时;
故答案为:80;
(2)休息后按原速继续前进行驶的时间为:(240﹣80)÷80=2(小时),
∴点E的坐标为(3.5,240),
设线段DE所表示的y与x之间的函数表达式为y=kx+b,则:
,解得,
∴线段DE所表示的y与x之间的函数表达式为:y=80x﹣40(1.5≤x≤3.5);
(3)接到通知后,汽车仍按原速行驶,则全程所需时间为:290÷80+0.5=4.125(小时),
12:00﹣8:00=4(小时),
4.125>4,
所以接到通知后,汽车仍按原速行驶不能准时到达.
23.(1)200×(10﹣8)=400(元)
答:截止到6月9日,该商店销售这种水果一共获利400元;
(2)设点B坐标为(a,400),根据题意得:
(10﹣8)×(600﹣a)+(10﹣8.5)×200=1200﹣400,
解这个方程,得a=350,
∴点B坐标为(350,400),
设线段BC所在直线对应的函数表达式为y=kx+b,则:
,解得,
∴线段BC所在直线对应的函数表达式为.
24.(1)m=300÷(180÷1.5)=2.5,
n=300÷[(300﹣180)÷1.5]=3.75,
故答案为:2.5;3.75;
(2)设甲车返回时y与x之间的函数关系式为y=kx+b,根据题意得:
,解得,
∴甲车返回时y与x之间的函数关系式是y=﹣100x+550(2.5≤x≤5.5);
(3)乙车的速度为:(300﹣180)÷1.5=80(千米/时),
甲车返回时的速度为:300÷(5.5﹣2.5)=100(千米/时),
根据题意得:80x﹣100(x﹣2.5)=190,解得x=3.
答:当x=3时,甲、乙两车相距190千米.
一、选择题.
1.A,B两地相距30km,甲乙两人沿同一条路线从A地到B地.如图,反映的是两人行进路程y(km)与行进时间t(h)之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上.以上说法正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.一条笔直的小路上顺次有A,B,C三个道口,甲、乙两人分别从A、B道口同时出发,各自匀速前往C道口,约定先到者在C道口等待,甲、乙两人间的距离y(米)与甲步行的时间x(分钟)之间的关系如图所示,则下列说法中错误的是( )
A.道口A、B相距660米 B.道口B、C相距1440米
C.甲的速度是70米/分 D.乙的速度是64米/分
3.如图,甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离为S(km)和行驶时间t(h)之间的函数关系的图象如图所示,则下列结论错误的是( )
A.A、B两地相距18km
B.甲在途中停留了0.5小时
C.全程行驶时间乙比甲少用了1小时
D.乙出发后0.5小时追上甲
4.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程y(km)与它们的行驶时间x(h)之间的函数关系.小欣同学结合图象得出如下结论:
①快车途中停留了0.5h;
②快车速度比慢车速度多20km/h;
③图中a=340;
④快车先到达目的地.
其中正确的是( )
A.①③ B.②③ C.②④ D.①④
5.如图,设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x小时后两车间的距离为y千米,y关于x的函数关系如图所示,则乙车的速度为( )
A.50千米/小时 B.45千米/小时
C.40千米/小时 D.35千米/小时
6.甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发后步行的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了22.5分钟;
③乙用9分钟追上甲;
④乙到达终点时,甲离终点还有270米.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.一辆货车从甲地匀速驶往乙地用了2.7h,到达后用了0.5h卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的1.5倍,货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示,则a等于( )
A.4.7 B.5.0 C.5.4 D.5.8
8.下列函数关系中,y随x的增大而减小的是( )
A.长方形的长一定时,其面积y与宽x的函数关系
B.高速公路上匀速行驶的汽车,其行驶的路程y与行驶时间x的函数关系
C.如图1,在平面直角坐标系中,点A(0,2)、B(1,0),△ABC的面积y与点C(x,0)的横坐标x(x<0)的函数关系
D.如图2,我市某一天的气温y(度)与时间x(时)的函数关系
9.在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法不正确的是( )
A.甲的速度保持不变
B.乙的平均速度比甲的平均速度大
C.在起跑后第180秒时,两人不相遇
D.在起跑后第50秒时,乙在甲的前面
10.甲、乙两车都从A地出发,都匀速行驶至B地,先到达的车停在B地休息.在整个行驶过程中,甲、乙两车离开A地的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.根据图中提供的信息,有下列说法:
①A,B两地相距300千米;
②甲车比乙车早出发1小时,且晚1小时到达B地;
③乙车只用了1.5小时就追上甲车;
④当甲、乙两车相距40千米时,t,,或小时.
其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了 分钟.
12.甲、乙两车从A地出发,沿同一条笔直的公路匀速驶向B地,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.已知两车到A地的距离y(km)与甲车出发的时间t(h)之间的函数关系分别如图中线段OC和折线D﹣E﹣F﹣C所示,则图中点C的坐标为 .
13.如图,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定快者比慢者每秒多跑 米.
14.小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象,则当小帅到达乙地时,小泽距乙地的距离为 千米.
15.小红从家到图书馆查阅资料然后返回,她离家的距离y与离家的时间x之间的对应关系如图所示,如果小红离家50分钟时离家的距离为0.3km,那么她在图书馆查阅资料的时间为 .
16.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B﹣C﹣D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下面几种说法:①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发小时再次与货车相遇;其中正确的是 .(填写序号)
17.一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,到达目的地停车,行驶过程中两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,则快车的速度是 千米/小时.
18.甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.给出下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有 .(把你认为正确结论的序号都填上)
三、解答题
19.某观光湖风景区,一观光轮与一巡逻艇同时从甲码头出发驶往乙码头,巡逻艇匀速往返于甲、乙两个码头之间,当观光轮到达乙码头时,巡逻艇也同时到达乙码头.设出发xh后,观光轮、巡逻艇离甲码头的距离分别为y1km、y2km.图中的线段OG、折线OABCDEFG分别表示y1、y2与x之间的函数关系.
(1)观光轮的速度是 km/h,巡逻艇的速度是 km/h;
(2)求整个过程中观光轮与巡逻艇的最大距离;
(3)求整个过程中观光轮与巡逻艇相遇的最短时间间隔.
20.小丽早晨6:00从家里出发,骑车去菜场买菜,然后从菜场返回家中.小丽离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,请根据图象回答下列问题:
(1)小丽去菜场途中的速度是多少?在菜场逗留了多长时间?
(2)小丽几点几分返回到家?
21.已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时;
(2)求甲、乙两车相遇后y与x之间的函数关系式;
(3)当甲车到达距B地90千米处时,求甲、乙两车之间的路程.
22.甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后.按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发x小时后离甲地的路程为y千米,图中折线OCDE表示接到通知前y与x之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为 千米/小时;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
23.某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(kg)之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题:
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图象中线段BC所在直线对应的函数表达式.
日期 销售记录
6月1日 库存600kg,成本价8元/kg,售价10元/kg(除了促销降价,其他时间售价保持不变).
6月9日 从6月1日至今,一共售出200kg.
6月10、11日 这两天以成本价促销,之后售价恢复到10元/kg.
6月12日 补充进货200kg,成本价8.5元/kg.
6月30日 800kg水果全部售完,一共获利1200元.
24.(张家港市模拟)甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,乙车匀速前往A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(小时),y与x之间的函数图象如图所示.
(1)图中,m= ,n= ;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在甲车返回到A地的过程中,当x为何值时,甲、乙两车相距190千米?
答案
一、选择题.
B.D.C.B.B.D.B.C.B.D.
二、填空题
11.40.
12.(8.4,672).
13.1.5
14.4
15.30分钟.
16.①③.
17.90.
18.①②③.
三、解答题
19.(1)观光轮的速度为:32÷2=16 (km/h),巡逻艇的速度为:(32×7)÷2=112( km/h);
故答案为:16;112;
(2)整个过程中观光轮与巡逻艇的最大距离:32﹣16(km);
(3)由题意可得:16x+112x=32×2,解得x;
,,即点B的坐标为(,0),点C的坐标为(,32),
设线段BC所表示的函数表达式为yBC=kx+b,则,解得,
∴yBC=112x﹣64,
易知y1=16x,
当y1=yBC时,112x﹣64=16x,解得x,.
答:最短时间间隔为 h.
20.(1)3000÷10=300(米/分),
40﹣10=30(分).
答:小丽去菜场途中的速度是300米/分,在菜场逗留了30分钟.
(2)设返回家时,y与x之间的函数关系式为y=kx+b(k≠0),
将(40,3000),(45,2000)代入y=kx+b,得:,
解得:,
∴y与x之间的函数关系式为y=﹣200x+11000.
当y=0时,﹣200x+11000=0,
解得:x=55,
∴小丽6点55分返回到家.
21.(1)由图可得,
乙车的速度为:270÷2﹣60=75(千米/时),
故答案为:75;
(2)a=270÷75=3.6,
故当a=3.6时,两车之间的距离为:60×3.6=216(千米),
b=270÷60=4.5,
当2<x≤3.6时,设y与x之间的函数关系式为y=kx+b,
,
解得,,
即当2<x≤3.6时,y与x之间的函数关系式为y=135x﹣270;
当3.6<x≤4.5时,设y与x之间的函数关系式为y=mx+n,
,
解得,,
即当3.6<x≤4.5时,y与x之间的函数关系式为y=60x;
由上可得,甲、乙两车相遇后,y与x之间的函数关系式为y;
(3)∵甲车到达距B地90千米处时,x3,
∴将x=3代入y=135x﹣270,得
y=135×3﹣270=135,
即当甲车到达距B地90千米处时,甲、乙两车之间的路程是135千米.
22.(1)由图象可知,休息前汽车行驶的速度为80千米/小时;
故答案为:80;
(2)休息后按原速继续前进行驶的时间为:(240﹣80)÷80=2(小时),
∴点E的坐标为(3.5,240),
设线段DE所表示的y与x之间的函数表达式为y=kx+b,则:
,解得,
∴线段DE所表示的y与x之间的函数表达式为:y=80x﹣40(1.5≤x≤3.5);
(3)接到通知后,汽车仍按原速行驶,则全程所需时间为:290÷80+0.5=4.125(小时),
12:00﹣8:00=4(小时),
4.125>4,
所以接到通知后,汽车仍按原速行驶不能准时到达.
23.(1)200×(10﹣8)=400(元)
答:截止到6月9日,该商店销售这种水果一共获利400元;
(2)设点B坐标为(a,400),根据题意得:
(10﹣8)×(600﹣a)+(10﹣8.5)×200=1200﹣400,
解这个方程,得a=350,
∴点B坐标为(350,400),
设线段BC所在直线对应的函数表达式为y=kx+b,则:
,解得,
∴线段BC所在直线对应的函数表达式为.
24.(1)m=300÷(180÷1.5)=2.5,
n=300÷[(300﹣180)÷1.5]=3.75,
故答案为:2.5;3.75;
(2)设甲车返回时y与x之间的函数关系式为y=kx+b,根据题意得:
,解得,
∴甲车返回时y与x之间的函数关系式是y=﹣100x+550(2.5≤x≤5.5);
(3)乙车的速度为:(300﹣180)÷1.5=80(千米/时),
甲车返回时的速度为:300÷(5.5﹣2.5)=100(千米/时),
根据题意得:80x﹣100(x﹣2.5)=190,解得x=3.
答:当x=3时,甲、乙两车相距190千米.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
