苏科版八年级数学上册 6.4用一次函数解决问题--销售问题同步练习(含答案)
文档属性
| 名称 | 苏科版八年级数学上册 6.4用一次函数解决问题--销售问题同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 10:59:51 | ||
图片预览


文档简介
6.4用一次函数解决问题--销售问题
一、选择题.
1.如图,l1反映了某公司产品的销售收入y1与销售量x的关系;l2反映了该公司产品的销售成本y2与销售量x的关系.根据图象判断,该公司盈利时,销售量( )
A.x<10 B.x=10 C.x>10 D.x≥10
2.我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
A.4小时 B.4.3小时 C.4.4小时 D.5小时
3.某超市以每千克0.8元的价格从批发市场购进若干千克西瓜,在销售了部分西瓜之后,余下的每千克降价0.3元,直至全部售完.销售金额y与售出西瓜的千克数x之间的关系如图所示,那么超市销售这批西瓜一共赚了( )
A.20元 B.32元 C.35元 D.36元
4.如图,购买一种苹果,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省( )
A.4 元 B.5 元 C.6 元 D.7 元
5.某快递公司每天上午7:00﹣8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为:( )
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为4件;
⑧8:00时,甲仓库内快件数为400件;
④7:20时,两仓库快递件数相同.
A.1个 B.2个 C.3个 D.4个
6.商场销售甲种服装每件的利润为40元,乙种服装每件的利润为30元.计划购进这两种服装共100件,其中甲种服装不少于65件,不超过75件.在5月1日当天对甲种服装以每件优惠a(0<a<10)元的价格进行优惠促销活动,乙种服装价格不变,则商场进货( )件甲种服装能获得最大利润.
A.65 B.70 C.75 D.100
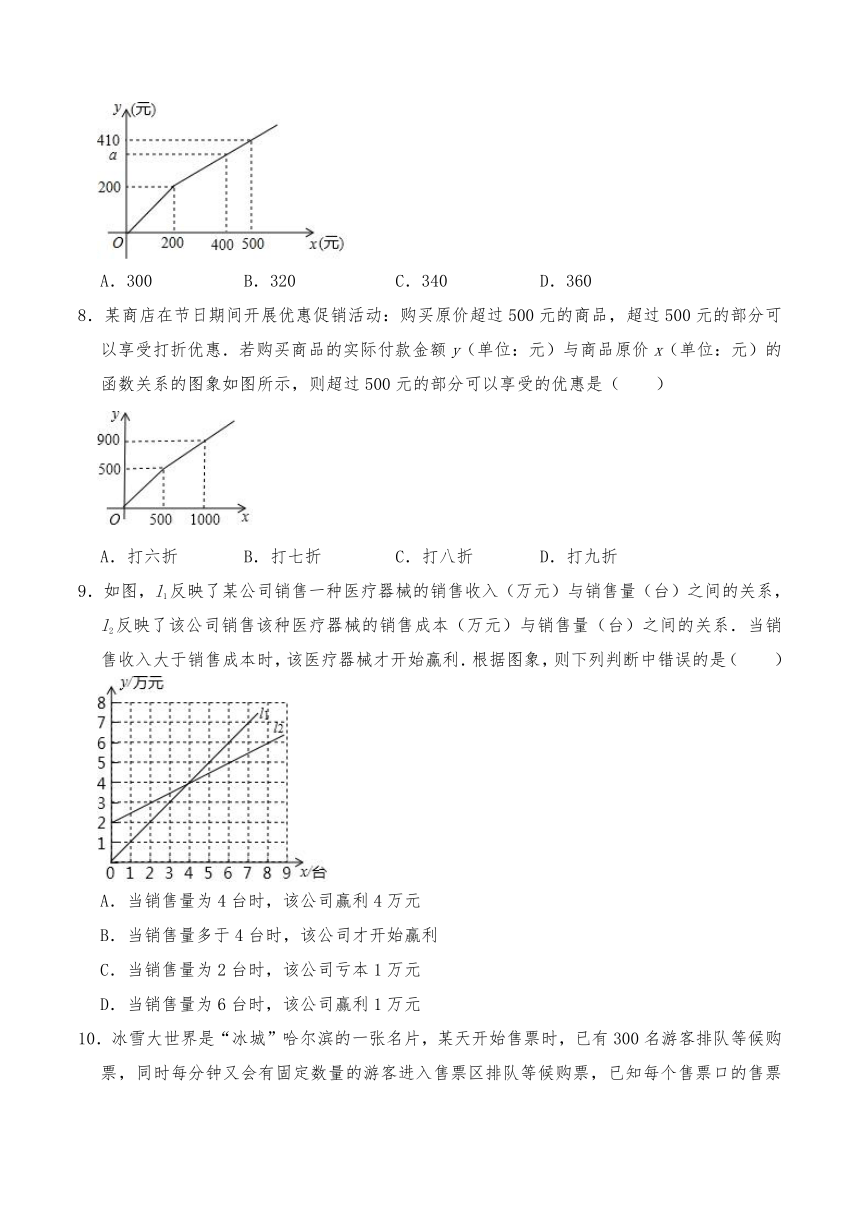
7.某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系的a图象如图所示,则图中a的值是( )
A.300 B.320 C.340 D.360
8.某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是( )
A.打六折 B.打七折 C.打八折 D.打九折
9.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
A.当销售量为4台时,该公司赢利4万元
B.当销售量多于4台时,该公司才开始赢利
C.当销售量为2台时,该公司亏本1万元
D.当销售量为6台时,该公司赢利1万元
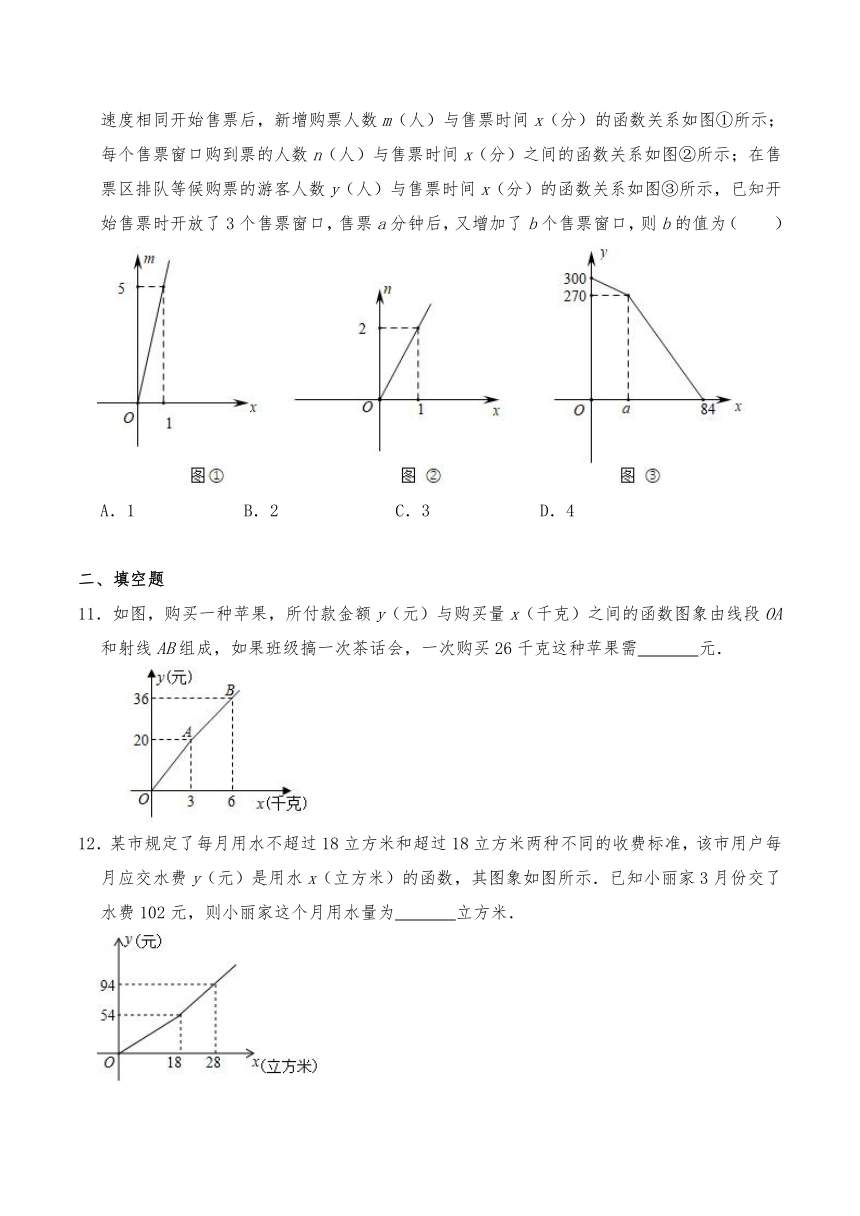
10.冰雪大世界是“冰城”哈尔滨的一张名片,某天开始售票时,已有300名游客排队等候购票,同时每分钟又会有固定数量的游客进入售票区排队等候购票,已知每个售票口的售票速度相同开始售票后,新增购票人数m(人)与售票时间x(分)的函数关系如图①所示;每个售票窗口购到票的人数n(人)与售票时间x(分)之间的函数关系如图②所示;在售票区排队等候购票的游客人数y(人)与售票时间x(分)的函数关系如图③所示,已知开始售票时开放了3个售票窗口,售票a分钟后,又增加了b个售票窗口,则b的值为( )
A.1 B.2 C.3 D.4
二、填空题
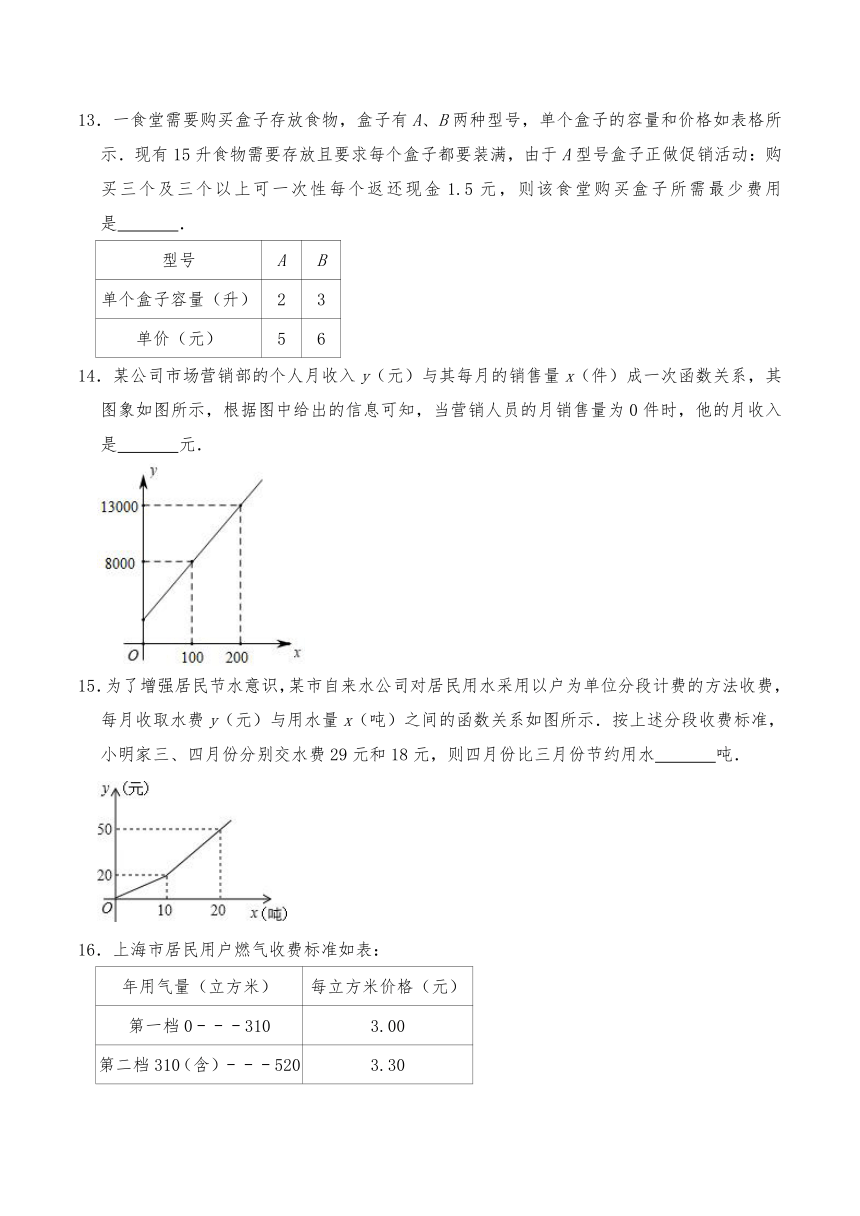
11.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,如果班级搞一次茶话会,一次购买26千克这种苹果需 元.
12.某市规定了每月用水不超过18立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为 立方米.
13.一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需最少费用是 .
型号 A B
单个盒子容量(升) 2 3
单价(元) 5 6
14.某公司市场营销部的个人月收入y(元)与其每月的销售量x(件)成一次函数关系,其图象如图所示,根据图中给出的信息可知,当营销人员的月销售量为0件时,他的月收入是 元.
15.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图所示.按上述分段收费标准,小明家三、四月份分别交水费29元和18元,则四月份比三月份节约用水 吨.
16.上海市居民用户燃气收费标准如表:
年用气量(立方米) 每立方米价格(元)
第一档0﹣﹣﹣310 3.00
第二档310(含)﹣﹣﹣520(含) 3.30
第三档520以上 4.20
某居民用户用气量在第一档,那么该用户每年燃气费y(元)与年用气量x(立方米)的函数关系式是 .
17.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是 万元.(利润=销售额﹣种植成本)
18.如图2是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是 .
①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
三、解答题
19.水果店张阿姨以每千克2元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额y(元)与销售量x(千克)之间的关系如图所示.
(1)情境中的变量有 .
(2)求降价后销售额y(元)与销售量x(千克)之间的函数表达式;
(3)当销售量为多少千克时,张阿姨销售此种水果的利润为150元?
20.“双十一”活动期间,某淘宝店欲将一批水果从A市运往B市,有火车和汽车两种运输方式,火车和汽车途中的平均速度分别为100千米/时和80千米/时.其他主要参考数据如表:
运输工具 途中平均损耗费用 (元/时) 途中综合费用 (元/千米) 装卸费用(元)
火车 200 15 2000
汽车 200 20 900
(1)①若A市与B市之间的距离为800千米,则火车运输的总费用是 元;汽车运输的总费用是
元;
②若A市与B市之间的距离为x千米,请直接写出火车运输的总费用y1(元)、汽车运输的总费用y2(元)分别与x(千米)之间的函数表达式.(总费用=途中损耗总费用+途中综合总费用+装卸费用)
(2)如果选择火车运输方式合算,那么x的取值范围是多少?
21.某经销商经销的冰箱二月份每台的售价比一月份每台的售价少500元,已知一月份卖出20台冰箱,二月份卖出25台冰箱,二月份的销售额比一月份多1万元.
(1)一、二月份冰箱每台售价各为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(y≤12),请问有几种进货方案?
(3)三月份为了促销,该经销商决定在二月份售价的基础上,每售出一台冰箱再返还顾客现金a元,而洗衣机按每台4400元销售,在这种情况下,若(2)中各方案获得的利润相同,则a= .(直接写出结果)
22.某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求该家具商场计划购进的餐桌、餐椅的进价分别为多少元?
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少?
23.某工厂生产A、B、C三种产品,这三种产品的生产数量均为x件.它们的单件成本和固定成本如表:
产品 单件成本(元/件) 固定成本(元)
A 0.1 1100
B 0.8 a
C b(b>0) 200
(注:总成本=单件成本×生产数量+固定成本)
(1)若产品A的总成本为yA,则yA关于x的函数表达式为 .
(2)当x=1000时,产品A、B的总成本相同.
①求a;
②当x≤2000时,产品C的总成本最低,求b的取值范围.
24.在“新冠病毒”防控期间,某医疗器械公司分两次购进酒精消毒液与额温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如表所示:
项目 购进数量(件) 购进所需费用(元)
酒精消毒液 额温枪
第一次 20 30 6200
第二次 30 20 4300
(1)求酒精消毒液和额温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件15元出售,额温枪以每件220元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于额温枪数量的9倍,求该公司销售完上述1000件商品获得的最大利润.
答案
一、选择题
C.C.B.C.C.C.C.C.A.B.
二、填空题
11..
12.30.
13.27元.
14.3000.
15.4.
16.y=3x(0≤x<310).
17.125.
18.①②④.
三、解答题
19.(1)答案为:销售额,销售量;
(2)将点A(40,160)、(80,260)代入一次函数表达式:y=kx+b并解得:
yx+60;
(3)第一种情况:降价前(0≤x≤40),利润为4x﹣2x=2x,
当2x=150时,x=75>40(不合题意)
第二种情况:降价后(x>40),利润为x+60﹣2xx+60
当x+60=150时,x=180.
答:当销售量为180千克时,张阿姨销售此种水果的利润为150元.
20.(1)①由题意可得,
火车运输的总费用是:200×(800÷100)+800×15+2000=15600(元),
汽车运输的总费用是:200×(800÷80)+800×20+900=18900(元),
故答案为:15600,18900;
②由题意可得,
火车运输的总费用y1(元)与x(千米)之间的函数表达式是:y1=200(x÷100)+15x+2000=17x+2000,
汽车运输的总费用y2(元)与x(千米)之间的函数表达式是:y2=200(x÷80)+20x+900=22.5x+900;
(2)令17x+2000<22.5x+900,
解得,x>200
答:如果选择火车运输方式合算,那么x的取值范围是x>200.
21.(1)设一月份冰箱每台售价x元,则二月份冰箱每台售价(x﹣500)元,
25(x﹣500)﹣20x=10000,
解得,x=4500,
∴x﹣500=4000,
答:一月份冰箱每台售价4500元,则二月份冰箱每台售价4000元;
(2)由题意可得,
3500y+4000(20﹣y)≤76000,
解得,y≥8,
∵y≤12且为整数,
∴y=8,9,10,11,12,
∴共有五种进货方案;
(3)设总获利w元,
w=(4000﹣3500﹣a)y+(4400﹣4000)(20﹣y)=(100﹣a)y+8000,
∵(2)中各方案获得的利润相同,
∴100﹣a=0,
解得,a=100,
故答案为:100.
22.(1)设每张餐桌的价格为a元,则每张餐椅的价格为(a﹣110)元,
,
解得,a=150
经检验,a=150是原分式方程的解,
则a﹣110=40,
答:该家具商场计划购进的餐桌、餐椅的进价分别为150元和40元;
(2)设购进餐桌x张,则购进餐椅(5x+20)张,销售利润为W元,
由题意得:x+5x+20 200,
解得,x 30
Wx (500﹣150﹣4×40)x (270﹣150)+(5x+20x×4)×(70﹣40)=245x+600,
∵k=245>0,
∴W随x的增大而增大,
∴当x=30时,W取得最大值,最大值为7950.此时5x+20=170,
答:购进餐桌30张、餐椅170张时,才能获得最大利润,最大利润是7950元.
23.(1)根据题意得:y=0.1x+1100;
故答案为:y=0.1x+1100.
(2)①由题意得0.8×1000+a=0.1×1000+1100,
解得a=400;
②当x=2000时,yC≤yA且yC≤yB,
即2000b+200≤2000×0.8+400;2000b+200≤2000×0.1+1100,
解得:0<b≤0.55.
24.(1)设酒精消毒液每件的进价为x元,额温枪每件的进价为y元,
根据题意得:,
解得:.
∴酒精消毒液每件的进价为10元,额温枪每件的进价为200元;
(2)设购进额温枪m件,获得的利润为W元,则购进酒精消毒液(1000﹣m)件,
根据题意得:
W=(15﹣10)(1000﹣m)+(220﹣200)m=15m+5000,
∵酒精消毒液的数量不少于额温枪数量的9倍,
∴1000﹣m≥9m,
解得:m≤100,
又∵在W=15m+5000中,k=15>0,
∴W的值随m的增大而增大,
∴当m=100时,W取最大值,最大值为15×100+5000=6500,
∴当购进购进酒精消毒液900件、额温枪100件时,销售利润最大,最大利润为6500元.
一、选择题.
1.如图,l1反映了某公司产品的销售收入y1与销售量x的关系;l2反映了该公司产品的销售成本y2与销售量x的关系.根据图象判断,该公司盈利时,销售量( )
A.x<10 B.x=10 C.x>10 D.x≥10
2.我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
A.4小时 B.4.3小时 C.4.4小时 D.5小时
3.某超市以每千克0.8元的价格从批发市场购进若干千克西瓜,在销售了部分西瓜之后,余下的每千克降价0.3元,直至全部售完.销售金额y与售出西瓜的千克数x之间的关系如图所示,那么超市销售这批西瓜一共赚了( )
A.20元 B.32元 C.35元 D.36元
4.如图,购买一种苹果,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省( )
A.4 元 B.5 元 C.6 元 D.7 元
5.某快递公司每天上午7:00﹣8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为:( )
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为4件;
⑧8:00时,甲仓库内快件数为400件;
④7:20时,两仓库快递件数相同.
A.1个 B.2个 C.3个 D.4个
6.商场销售甲种服装每件的利润为40元,乙种服装每件的利润为30元.计划购进这两种服装共100件,其中甲种服装不少于65件,不超过75件.在5月1日当天对甲种服装以每件优惠a(0<a<10)元的价格进行优惠促销活动,乙种服装价格不变,则商场进货( )件甲种服装能获得最大利润.
A.65 B.70 C.75 D.100
7.某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系的a图象如图所示,则图中a的值是( )
A.300 B.320 C.340 D.360
8.某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是( )
A.打六折 B.打七折 C.打八折 D.打九折
9.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
A.当销售量为4台时,该公司赢利4万元
B.当销售量多于4台时,该公司才开始赢利
C.当销售量为2台时,该公司亏本1万元
D.当销售量为6台时,该公司赢利1万元
10.冰雪大世界是“冰城”哈尔滨的一张名片,某天开始售票时,已有300名游客排队等候购票,同时每分钟又会有固定数量的游客进入售票区排队等候购票,已知每个售票口的售票速度相同开始售票后,新增购票人数m(人)与售票时间x(分)的函数关系如图①所示;每个售票窗口购到票的人数n(人)与售票时间x(分)之间的函数关系如图②所示;在售票区排队等候购票的游客人数y(人)与售票时间x(分)的函数关系如图③所示,已知开始售票时开放了3个售票窗口,售票a分钟后,又增加了b个售票窗口,则b的值为( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,如果班级搞一次茶话会,一次购买26千克这种苹果需 元.
12.某市规定了每月用水不超过18立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为 立方米.
13.一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需最少费用是 .
型号 A B
单个盒子容量(升) 2 3
单价(元) 5 6
14.某公司市场营销部的个人月收入y(元)与其每月的销售量x(件)成一次函数关系,其图象如图所示,根据图中给出的信息可知,当营销人员的月销售量为0件时,他的月收入是 元.
15.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费的方法收费,每月收取水费y(元)与用水量x(吨)之间的函数关系如图所示.按上述分段收费标准,小明家三、四月份分别交水费29元和18元,则四月份比三月份节约用水 吨.
16.上海市居民用户燃气收费标准如表:
年用气量(立方米) 每立方米价格(元)
第一档0﹣﹣﹣310 3.00
第二档310(含)﹣﹣﹣520(含) 3.30
第三档520以上 4.20
某居民用户用气量在第一档,那么该用户每年燃气费y(元)与年用气量x(立方米)的函数关系式是 .
17.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是 万元.(利润=销售额﹣种植成本)
18.如图2是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是 .
①第24天的销售量为200件;
②第10天销售一件产品的利润是15元;
③第12天与第30天这两天的日销售利润相等;
④第30天的日销售利润是750元.
三、解答题
19.水果店张阿姨以每千克2元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额y(元)与销售量x(千克)之间的关系如图所示.
(1)情境中的变量有 .
(2)求降价后销售额y(元)与销售量x(千克)之间的函数表达式;
(3)当销售量为多少千克时,张阿姨销售此种水果的利润为150元?
20.“双十一”活动期间,某淘宝店欲将一批水果从A市运往B市,有火车和汽车两种运输方式,火车和汽车途中的平均速度分别为100千米/时和80千米/时.其他主要参考数据如表:
运输工具 途中平均损耗费用 (元/时) 途中综合费用 (元/千米) 装卸费用(元)
火车 200 15 2000
汽车 200 20 900
(1)①若A市与B市之间的距离为800千米,则火车运输的总费用是 元;汽车运输的总费用是
元;
②若A市与B市之间的距离为x千米,请直接写出火车运输的总费用y1(元)、汽车运输的总费用y2(元)分别与x(千米)之间的函数表达式.(总费用=途中损耗总费用+途中综合总费用+装卸费用)
(2)如果选择火车运输方式合算,那么x的取值范围是多少?
21.某经销商经销的冰箱二月份每台的售价比一月份每台的售价少500元,已知一月份卖出20台冰箱,二月份卖出25台冰箱,二月份的销售额比一月份多1万元.
(1)一、二月份冰箱每台售价各为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(y≤12),请问有几种进货方案?
(3)三月份为了促销,该经销商决定在二月份售价的基础上,每售出一台冰箱再返还顾客现金a元,而洗衣机按每台4400元销售,在这种情况下,若(2)中各方案获得的利润相同,则a= .(直接写出结果)
22.某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求该家具商场计划购进的餐桌、餐椅的进价分别为多少元?
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少?
23.某工厂生产A、B、C三种产品,这三种产品的生产数量均为x件.它们的单件成本和固定成本如表:
产品 单件成本(元/件) 固定成本(元)
A 0.1 1100
B 0.8 a
C b(b>0) 200
(注:总成本=单件成本×生产数量+固定成本)
(1)若产品A的总成本为yA,则yA关于x的函数表达式为 .
(2)当x=1000时,产品A、B的总成本相同.
①求a;
②当x≤2000时,产品C的总成本最低,求b的取值范围.
24.在“新冠病毒”防控期间,某医疗器械公司分两次购进酒精消毒液与额温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如表所示:
项目 购进数量(件) 购进所需费用(元)
酒精消毒液 额温枪
第一次 20 30 6200
第二次 30 20 4300
(1)求酒精消毒液和额温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件15元出售,额温枪以每件220元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于额温枪数量的9倍,求该公司销售完上述1000件商品获得的最大利润.
答案
一、选择题
C.C.B.C.C.C.C.C.A.B.
二、填空题
11..
12.30.
13.27元.
14.3000.
15.4.
16.y=3x(0≤x<310).
17.125.
18.①②④.
三、解答题
19.(1)答案为:销售额,销售量;
(2)将点A(40,160)、(80,260)代入一次函数表达式:y=kx+b并解得:
yx+60;
(3)第一种情况:降价前(0≤x≤40),利润为4x﹣2x=2x,
当2x=150时,x=75>40(不合题意)
第二种情况:降价后(x>40),利润为x+60﹣2xx+60
当x+60=150时,x=180.
答:当销售量为180千克时,张阿姨销售此种水果的利润为150元.
20.(1)①由题意可得,
火车运输的总费用是:200×(800÷100)+800×15+2000=15600(元),
汽车运输的总费用是:200×(800÷80)+800×20+900=18900(元),
故答案为:15600,18900;
②由题意可得,
火车运输的总费用y1(元)与x(千米)之间的函数表达式是:y1=200(x÷100)+15x+2000=17x+2000,
汽车运输的总费用y2(元)与x(千米)之间的函数表达式是:y2=200(x÷80)+20x+900=22.5x+900;
(2)令17x+2000<22.5x+900,
解得,x>200
答:如果选择火车运输方式合算,那么x的取值范围是x>200.
21.(1)设一月份冰箱每台售价x元,则二月份冰箱每台售价(x﹣500)元,
25(x﹣500)﹣20x=10000,
解得,x=4500,
∴x﹣500=4000,
答:一月份冰箱每台售价4500元,则二月份冰箱每台售价4000元;
(2)由题意可得,
3500y+4000(20﹣y)≤76000,
解得,y≥8,
∵y≤12且为整数,
∴y=8,9,10,11,12,
∴共有五种进货方案;
(3)设总获利w元,
w=(4000﹣3500﹣a)y+(4400﹣4000)(20﹣y)=(100﹣a)y+8000,
∵(2)中各方案获得的利润相同,
∴100﹣a=0,
解得,a=100,
故答案为:100.
22.(1)设每张餐桌的价格为a元,则每张餐椅的价格为(a﹣110)元,
,
解得,a=150
经检验,a=150是原分式方程的解,
则a﹣110=40,
答:该家具商场计划购进的餐桌、餐椅的进价分别为150元和40元;
(2)设购进餐桌x张,则购进餐椅(5x+20)张,销售利润为W元,
由题意得:x+5x+20 200,
解得,x 30
Wx (500﹣150﹣4×40)x (270﹣150)+(5x+20x×4)×(70﹣40)=245x+600,
∵k=245>0,
∴W随x的增大而增大,
∴当x=30时,W取得最大值,最大值为7950.此时5x+20=170,
答:购进餐桌30张、餐椅170张时,才能获得最大利润,最大利润是7950元.
23.(1)根据题意得:y=0.1x+1100;
故答案为:y=0.1x+1100.
(2)①由题意得0.8×1000+a=0.1×1000+1100,
解得a=400;
②当x=2000时,yC≤yA且yC≤yB,
即2000b+200≤2000×0.8+400;2000b+200≤2000×0.1+1100,
解得:0<b≤0.55.
24.(1)设酒精消毒液每件的进价为x元,额温枪每件的进价为y元,
根据题意得:,
解得:.
∴酒精消毒液每件的进价为10元,额温枪每件的进价为200元;
(2)设购进额温枪m件,获得的利润为W元,则购进酒精消毒液(1000﹣m)件,
根据题意得:
W=(15﹣10)(1000﹣m)+(220﹣200)m=15m+5000,
∵酒精消毒液的数量不少于额温枪数量的9倍,
∴1000﹣m≥9m,
解得:m≤100,
又∵在W=15m+5000中,k=15>0,
∴W的值随m的增大而增大,
∴当m=100时,W取最大值,最大值为15×100+5000=6500,
∴当购进购进酒精消毒液900件、额温枪100件时,销售利润最大,最大利润为6500元.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
