苏科版八年级数学上册 第5章平面直角坐标系单元测试卷(含答案)
文档属性
| 名称 | 苏科版八年级数学上册 第5章平面直角坐标系单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 11:00:53 | ||
图片预览




文档简介
第5章平面直角坐标系单元测试卷
一、选择题(本大题共10小题,每小题2分,共20分).
1.将点M(1,1)向左平移1个单位长度,向下平移2个单位到点N,那么点N的坐标是( )
A.(0,﹣1) B.(0,﹣2) C.(0,﹣3) D.(1,1)
2.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形( )
A.向左平移3个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移3个单位
3.在平面直角坐标系中,点G的坐标是(﹣2,1),连接OG,将线段OG绕原点O旋转180°,得到对应线段OG',则点G'的坐标为( )
A.(2,﹣1) B.(2,1) C.(1,﹣2) D.(﹣2,﹣1)
4.已知点A(m,n),且有mn≤0,则点A一定不在( )
A.第一象限 B.第二象限 C.第四象限 D.坐标轴上
5.已知(a﹣3)2+|b﹣4|=0,则点M(a,b)的坐标为( )
A.(3,4) B.(﹣3,4) C.(﹣3,﹣4) D.(3,﹣4)
6.在平面直角坐标系中,平行于坐标轴的线段PQ=5,若点P坐标是(﹣2,1),则点Q不在第( )象限.
A.一 B.二 C.三 D.四
7.如图,如果★的坐标是(6,3),◆的坐标是(4,7),那么⊙的坐标是( )
A.(7,4) B.(5,7) C.(8,4) D.(8,5)
8.已知坐标平面内,线段AB∥x轴,点A(﹣2,4),AB=1,则B点坐标为( )
A.(﹣1,4) B.(﹣3,4)
C.(﹣1,4)或(﹣3,4) D.(﹣2,3)或(﹣2,5)
9.预备知识:线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为()应用:设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为( )
A.(﹣1,1) B.(﹣2,4) C.(﹣2,1) D.(﹣1,4)
10.甲、乙两名同学下棋,甲执圆子,乙执方子,如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示,甲将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,甲放的位置是( )
A.(﹣2,1) B.(﹣1,1) C.(﹣1,0) D.(﹣1,2)
二、填空题(本大题共8小题,每小题2分,共16分.)
11.如图,在平面直角坐标系中,点A的坐标是(2,1),点B的坐标是(2,0).作点B关于OA的对称点B′,则点B′的坐标是( , ).
12.已知,平面直角坐标系中点A(﹣5,3)关于直线x=1的对称点是 .
13.点P(1,﹣2)关于直线y=1轴对称的点的坐标是 .
14.如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为 .
15.如果将电影票上“8排5号”简记为(8,5),那么“11排10号”可表示为 ;(5,6)表示的含义是 .
16.已知平面内有一点A的横坐标为﹣6,且到原点的距离等于10,则A点的坐标为 .
17.如图,直线l1⊥l2,在某平面直角坐标系中,x轴∥11,y轴∥l2,点A的坐标为(﹣1,2),点B的坐标为(2,﹣1),那么点C在第 象限.
18.在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是 .
三、解答题(本大题共8小题,共64分.)
19.如图,在正方形网格中,若点A的坐标是(1,2),点B的坐标是(2,1).
(1)依题意,在图中建立平面直角坐标系;
(2)图中点C的坐标是 ,
(3)若点D的坐标为(0,3),在图中标出点D的位置;
(4)将点B向左平移3个单位长度,再向上平移1个单位长度,则所得的点B'的坐标是 ,△AB'C的面积为 .
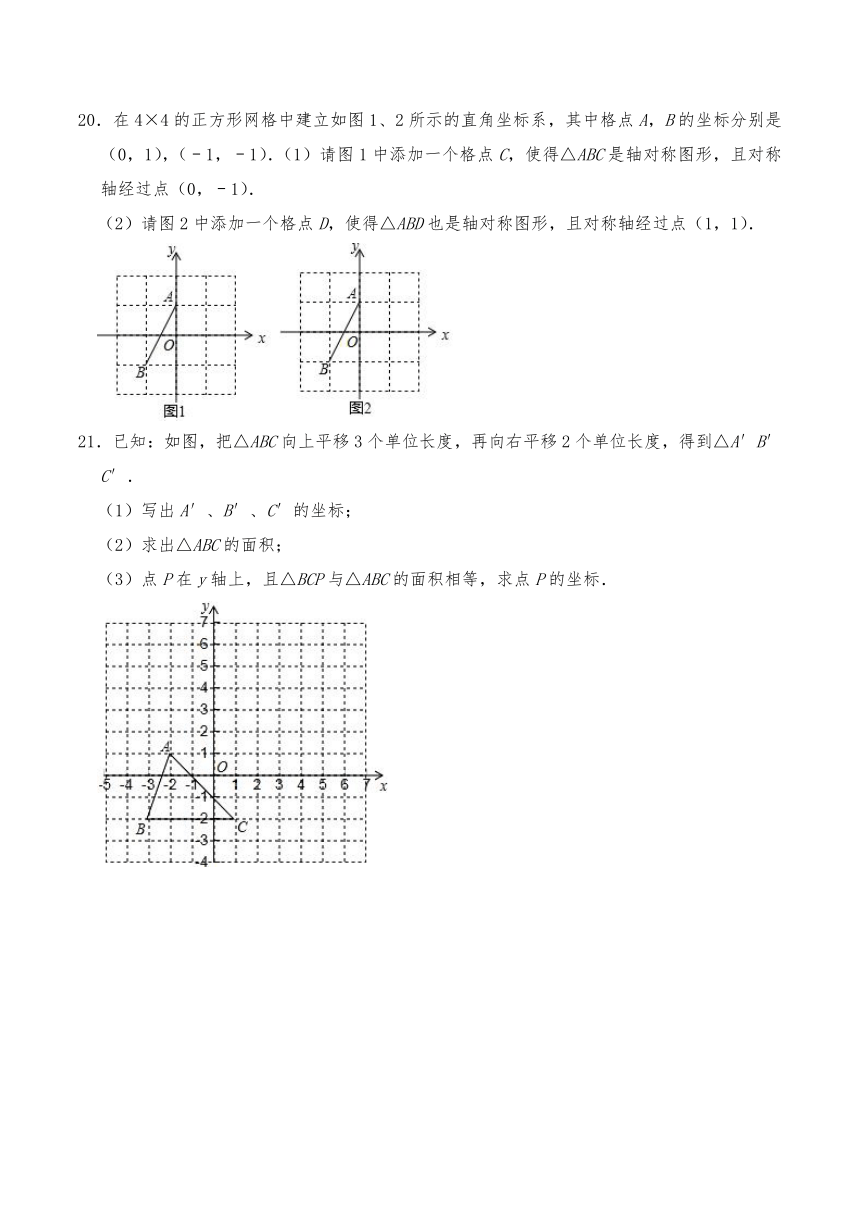
20.在4×4的正方形网格中建立如图1、2所示的直角坐标系,其中格点A,B的坐标分别是(0,1),(﹣1,﹣1).(1)请图1中添加一个格点C,使得△ABC是轴对称图形,且对称轴经过点(0,﹣1).
(2)请图2中添加一个格点D,使得△ABD也是轴对称图形,且对称轴经过点(1,1).
21.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
22.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标.
23.问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
24.在平面直角坐标系中,有点A(a+1,2),B(﹣a﹣5,2a+1).
(1)若线段AB∥y轴,求点A、B的坐标;
(2)当点B在第二、四象限的角平分线上时,求A点坐标.
25.已知三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图
(1)分别写出点B、B'的坐标:B ,B' ;
(2)若点P(a,b)是三角形ABC内部一点,则平移后三角形A'B'C'内的对应点P'的坐标为 ;
(3)求三角形ABC的面积.
26.对于实数a,b定义两种新运算“※”和“*”:a※b=a+kb,a*b=ka+b(其中k为常数,且k≠0),若对于平面直角坐标系xOy中的点P(a,b),有点P′的坐标(a※b,a*b)与之对应,则称点P的“k衍生点”为点P′.例如:P(1,3)的“2衍生点”为P′(1+2×3,2×1+3),即P′(7,5).
(1)点P(﹣1,5)的“3衍生点”的坐标为 ;
(2)若点P的“5衍生点”P的坐标为(9,﹣3),求点P的坐标;
(3)若点P的“k衍生点”为点P′,且直线PP′平行于y轴,线段PP′的长度为线段OP长度的3倍,求k的值.
答案
一、选择题
A.B.A.A.A.D.D.C.A.B.
二、填空题
11.,.
12.(7,3)
13.(1,4).
14.HELLO.
15.(11,10);5排6号.
16.(﹣6,8)或(﹣6,﹣8).
17.三.
18.﹣1或5.
三、解答题
19.(1)如图所示.
(2)C(﹣1,﹣1).
(3)如图所示:D点即为所求;
(4)B'(﹣1,2);
△AB'C的面积3.
故答案为:(﹣1,﹣1);(﹣1,2); 3.
20.(1)如图,点C即为所求.
(2)如图,点D即为所求.
21.(1)如图所示:A′(0,4)、B′(﹣1,1)、C′(3,1);
(2)S△ABC(3+1)×3=6;
(3)设点P坐标为(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得4×|y+2|=6,
解得y=1或y=﹣5,
所以点P的坐标为(0,1)或(0,﹣5).
22.(1)如图,
(2)点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1).
23.【应用】:
(1)AB的长度为|﹣1﹣2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
故答案为:(1,2)或(1,﹣2).
【拓展】:
(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.
故答案为:4或8.
24.(1)∵线段AB∥y轴,∴a+1=﹣a﹣5,
解得:a=﹣3,
∴点A(﹣2,2),B(﹣2,﹣5);
(2)∵点B(﹣a﹣5,2a+1)在第二、四象限的角平分线上,
∴(﹣a﹣5)+(2a+1)=0.
解得a=4.
∴点A的坐标为(5,2).
25.(1)观察图象可知B(3,﹣4),B′(﹣2,0).
故答案为:(3,﹣4),(﹣2,0).
(2)由题意△A′B′C′是由△ABC向左平移5个单位,向上平移4个单位得到,
∴P′(a﹣5,b+4).
故答案为(a﹣5,b+4).
(3)S△ABC=4×42×44×12×3=7.
26.(1)点P(﹣1,5)的“3衍生点”P′的坐标为(﹣1+3X5,﹣1X3+5),即(14,2),
故答案为:(14,2);
(2)设P(x,y)
依题意,得方程组.
解得.
∴点P(﹣1,2);
(3)设P(a,b),则P′的坐标为(a+kb,ka+b).
∵PP′平行于y轴
∴a=a+kb,即kb=0,
又∵k≠0,
∴b=0.
∴点P的坐标为(a,0),点P'的坐标为(a,ka),
∴线段PP′的长度为|ka|.
∴线段OP的长为|a|.
根据题意,有|PP′|=3|OP|,
∴|ka|=3|a|.
∴k=±3.
一、选择题(本大题共10小题,每小题2分,共20分).
1.将点M(1,1)向左平移1个单位长度,向下平移2个单位到点N,那么点N的坐标是( )
A.(0,﹣1) B.(0,﹣2) C.(0,﹣3) D.(1,1)
2.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都加上3,则所得图形与原图形的关系是:将原图形( )
A.向左平移3个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移3个单位
3.在平面直角坐标系中,点G的坐标是(﹣2,1),连接OG,将线段OG绕原点O旋转180°,得到对应线段OG',则点G'的坐标为( )
A.(2,﹣1) B.(2,1) C.(1,﹣2) D.(﹣2,﹣1)
4.已知点A(m,n),且有mn≤0,则点A一定不在( )
A.第一象限 B.第二象限 C.第四象限 D.坐标轴上
5.已知(a﹣3)2+|b﹣4|=0,则点M(a,b)的坐标为( )
A.(3,4) B.(﹣3,4) C.(﹣3,﹣4) D.(3,﹣4)
6.在平面直角坐标系中,平行于坐标轴的线段PQ=5,若点P坐标是(﹣2,1),则点Q不在第( )象限.
A.一 B.二 C.三 D.四
7.如图,如果★的坐标是(6,3),◆的坐标是(4,7),那么⊙的坐标是( )
A.(7,4) B.(5,7) C.(8,4) D.(8,5)
8.已知坐标平面内,线段AB∥x轴,点A(﹣2,4),AB=1,则B点坐标为( )
A.(﹣1,4) B.(﹣3,4)
C.(﹣1,4)或(﹣3,4) D.(﹣2,3)或(﹣2,5)
9.预备知识:线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为()应用:设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为( )
A.(﹣1,1) B.(﹣2,4) C.(﹣2,1) D.(﹣1,4)
10.甲、乙两名同学下棋,甲执圆子,乙执方子,如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示,甲将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,甲放的位置是( )
A.(﹣2,1) B.(﹣1,1) C.(﹣1,0) D.(﹣1,2)
二、填空题(本大题共8小题,每小题2分,共16分.)
11.如图,在平面直角坐标系中,点A的坐标是(2,1),点B的坐标是(2,0).作点B关于OA的对称点B′,则点B′的坐标是( , ).
12.已知,平面直角坐标系中点A(﹣5,3)关于直线x=1的对称点是 .
13.点P(1,﹣2)关于直线y=1轴对称的点的坐标是 .
14.如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为 .
15.如果将电影票上“8排5号”简记为(8,5),那么“11排10号”可表示为 ;(5,6)表示的含义是 .
16.已知平面内有一点A的横坐标为﹣6,且到原点的距离等于10,则A点的坐标为 .
17.如图,直线l1⊥l2,在某平面直角坐标系中,x轴∥11,y轴∥l2,点A的坐标为(﹣1,2),点B的坐标为(2,﹣1),那么点C在第 象限.
18.在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是 .
三、解答题(本大题共8小题,共64分.)
19.如图,在正方形网格中,若点A的坐标是(1,2),点B的坐标是(2,1).
(1)依题意,在图中建立平面直角坐标系;
(2)图中点C的坐标是 ,
(3)若点D的坐标为(0,3),在图中标出点D的位置;
(4)将点B向左平移3个单位长度,再向上平移1个单位长度,则所得的点B'的坐标是 ,△AB'C的面积为 .
20.在4×4的正方形网格中建立如图1、2所示的直角坐标系,其中格点A,B的坐标分别是(0,1),(﹣1,﹣1).(1)请图1中添加一个格点C,使得△ABC是轴对称图形,且对称轴经过点(0,﹣1).
(2)请图2中添加一个格点D,使得△ABD也是轴对称图形,且对称轴经过点(1,1).
21.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
22.如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标.
23.问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
24.在平面直角坐标系中,有点A(a+1,2),B(﹣a﹣5,2a+1).
(1)若线段AB∥y轴,求点A、B的坐标;
(2)当点B在第二、四象限的角平分线上时,求A点坐标.
25.已知三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图
(1)分别写出点B、B'的坐标:B ,B' ;
(2)若点P(a,b)是三角形ABC内部一点,则平移后三角形A'B'C'内的对应点P'的坐标为 ;
(3)求三角形ABC的面积.
26.对于实数a,b定义两种新运算“※”和“*”:a※b=a+kb,a*b=ka+b(其中k为常数,且k≠0),若对于平面直角坐标系xOy中的点P(a,b),有点P′的坐标(a※b,a*b)与之对应,则称点P的“k衍生点”为点P′.例如:P(1,3)的“2衍生点”为P′(1+2×3,2×1+3),即P′(7,5).
(1)点P(﹣1,5)的“3衍生点”的坐标为 ;
(2)若点P的“5衍生点”P的坐标为(9,﹣3),求点P的坐标;
(3)若点P的“k衍生点”为点P′,且直线PP′平行于y轴,线段PP′的长度为线段OP长度的3倍,求k的值.
答案
一、选择题
A.B.A.A.A.D.D.C.A.B.
二、填空题
11.,.
12.(7,3)
13.(1,4).
14.HELLO.
15.(11,10);5排6号.
16.(﹣6,8)或(﹣6,﹣8).
17.三.
18.﹣1或5.
三、解答题
19.(1)如图所示.
(2)C(﹣1,﹣1).
(3)如图所示:D点即为所求;
(4)B'(﹣1,2);
△AB'C的面积3.
故答案为:(﹣1,﹣1);(﹣1,2); 3.
20.(1)如图,点C即为所求.
(2)如图,点D即为所求.
21.(1)如图所示:A′(0,4)、B′(﹣1,1)、C′(3,1);
(2)S△ABC(3+1)×3=6;
(3)设点P坐标为(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得4×|y+2|=6,
解得y=1或y=﹣5,
所以点P的坐标为(0,1)或(0,﹣5).
22.(1)如图,
(2)点A′的坐标为(4,0),点B′的坐标为(﹣1,﹣4),点C′的坐标为(﹣3,﹣1).
23.【应用】:
(1)AB的长度为|﹣1﹣2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).
故答案为:(1,2)或(1,﹣2).
【拓展】:
(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.
故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;
当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.
故答案为:4或8.
24.(1)∵线段AB∥y轴,∴a+1=﹣a﹣5,
解得:a=﹣3,
∴点A(﹣2,2),B(﹣2,﹣5);
(2)∵点B(﹣a﹣5,2a+1)在第二、四象限的角平分线上,
∴(﹣a﹣5)+(2a+1)=0.
解得a=4.
∴点A的坐标为(5,2).
25.(1)观察图象可知B(3,﹣4),B′(﹣2,0).
故答案为:(3,﹣4),(﹣2,0).
(2)由题意△A′B′C′是由△ABC向左平移5个单位,向上平移4个单位得到,
∴P′(a﹣5,b+4).
故答案为(a﹣5,b+4).
(3)S△ABC=4×42×44×12×3=7.
26.(1)点P(﹣1,5)的“3衍生点”P′的坐标为(﹣1+3X5,﹣1X3+5),即(14,2),
故答案为:(14,2);
(2)设P(x,y)
依题意,得方程组.
解得.
∴点P(﹣1,2);
(3)设P(a,b),则P′的坐标为(a+kb,ka+b).
∵PP′平行于y轴
∴a=a+kb,即kb=0,
又∵k≠0,
∴b=0.
∴点P的坐标为(a,0),点P'的坐标为(a,ka),
∴线段PP′的长度为|ka|.
∴线段OP的长为|a|.
根据题意,有|PP′|=3|OP|,
∴|ka|=3|a|.
∴k=±3.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
