苏科版八年级数学上册第5章平面直角坐标系单元测试(含答案)
文档属性
| 名称 | 苏科版八年级数学上册第5章平面直角坐标系单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 119.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 11:02:09 | ||
图片预览



文档简介
第5章平面直角坐标系单元测试
一、选择题(本大题共10小题,每小题2分,共20分).
1.已知点P(2,m)在x轴上,则m的值是( )
A.2 B.0 C.﹣2 D.1
2.在平面直角坐标系中,点(﹣2,﹣3)到x轴的距离是( )
A.﹣2 B.﹣3 C.2 D.3
3.在平面直角坐标系中,下列各点在第三象限的是( )
A.(1,2) B.(﹣2,1) C.(2,﹣1) D.(﹣1,﹣2)
4.棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图是局象棋残局,若在中国象棋盘上建立平面直角坐标系,使表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示“炮”的点的坐标为( )
A.(1,3) B.(3,1) C.(2,3) D.(1,2)
5.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3) B.(1,﹣3) C.(9,8) D.(﹣9,﹣8)
6.若点(a,b)在第四象限,则( )
A.a>b B.a≥b C.a<b D.无法判定 a,b 之间的大小
7.在直角坐标平面内,已知点B和点A(3,4)关于x轴对称,那么点B的坐标( )
A.(3,4) B.(﹣3,﹣4) C.(3,﹣4) D.(﹣3,4)
8.下列语句正确的是( )
A.平行于x轴的直线上所有点的横坐标都相同
B.(﹣3,5)与(5,﹣3)表示两个不同的点
C.若点P(a,b)在y轴上,则b=0
D.若点P(﹣3,4),则P到x轴的距离为3
9.如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为(4,2),四号暗堡的坐标为(﹣2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( )
A.A处 B.B处 C.C处 D.D处
10.点(﹣7,0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
二、填空题(本大题共8小题,每小题2分,共16分.)
11.在直角坐标系中,已知点P的坐标为(﹣3,﹣1),则点P在第 象限.
12.若点P(2m+4,m﹣1)在x轴上,则m= .
13.若点N(a+5,a﹣2)在y轴上,则a= ,N点的坐标为 .
14.如果座位表上“6列3行”记作(6,3),那么(4,3)表示 .
15.在平面直角坐标系中,点P(4,2)关于x轴的对称点的坐标是 .
16.已知点A(m,n)在第四象限,那么点B(m,﹣n)在第 象限.
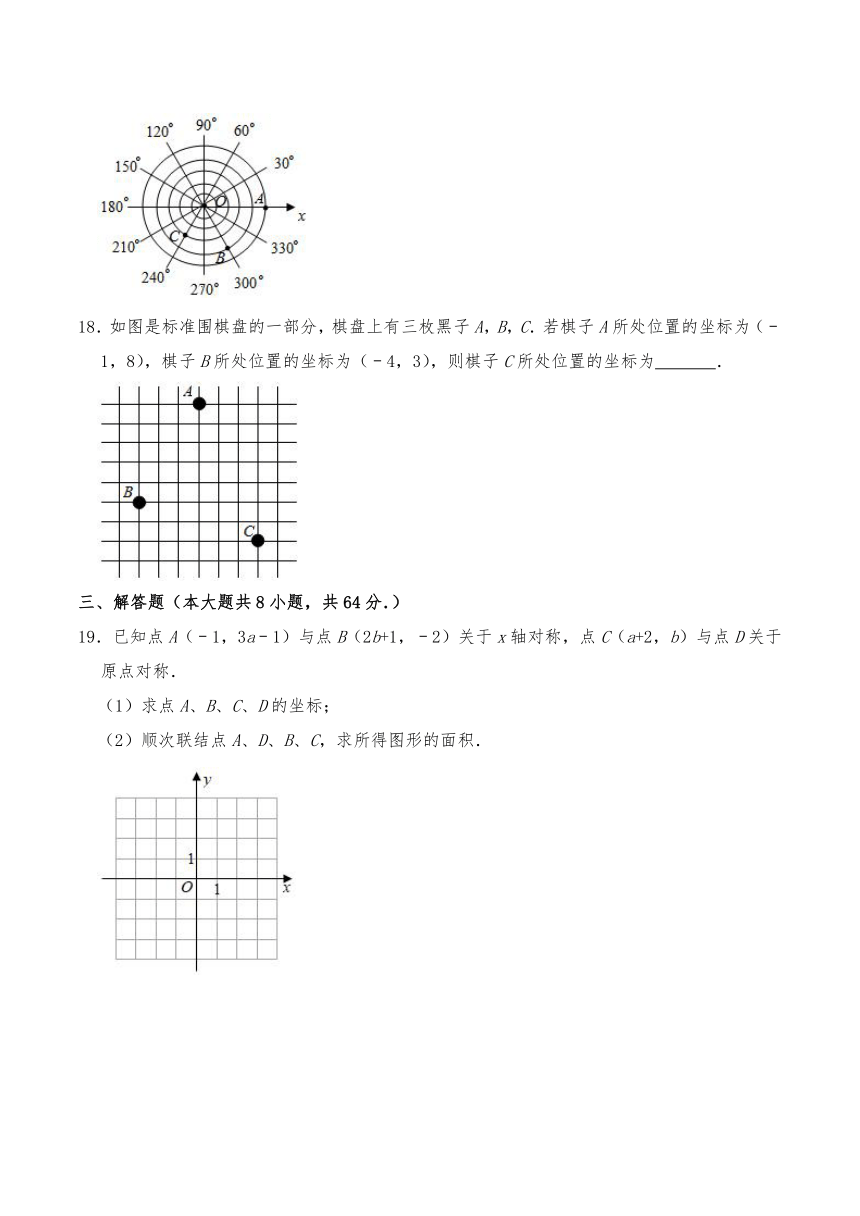
17.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为 .
18.如图是标准围棋盘的一部分,棋盘上有三枚黑子A,B,C.若棋子A所处位置的坐标为(﹣1,8),棋子B所处位置的坐标为(﹣4,3),则棋子C所处位置的坐标为 .
三、解答题(本大题共8小题,共64分.)
19.已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次联结点A、D、B、C,求所得图形的面积.
20.在平面直角坐标系中,已知点M(m﹣1,2m+3).
(1)若点M在y轴上,求m的值.
(2)若点N(﹣3,2),且直线MN∥y轴,求线段MN的长.
21.已知点P(﹣3a﹣4,2+a),解答下列各题:
(1)若点P在x轴上,试求出点P的坐标;
(2)若Q(5,8),且PQ∥y轴,试求出点P的坐标.
22.(1)在直角坐标系中,将点A(﹣2,3)关于x轴的对称点B向右平移3个单位长度得到点C,求C点的坐标.
(2)已知点P(0,m)在y轴负半轴上,试判断M(﹣m,﹣m+1)落在第几象限.
23.如图,在所给的平面直角坐标系中,写出点A、B、C、D、E的坐标.
24.如图是天安门广场周围的主要景点分布示意图.在此图中建立平面直角坐标系,表示故宫的点坐标为(0,﹣1),表示美术馆的点的坐标为(2,2),并写出其余各景点的坐标.
25.如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标.
26.如图,在直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位,再向右平移5个单位得到△A′B′C′,并写出C′的坐标.
答案
一、选择题
B.D.D.A.A.A.C.B.B.B.
二、填空题
11.三.
12.1.
13.﹣5;(0,﹣7).
14.4列3行.
15.(4,﹣2).
16.一.
17.(3,240°).
18.(2,1).
三、解答题
19.解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,
∴2b+1=﹣1,3a﹣1=2,
解得a=1,b=﹣1,
∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),
∵点C(a+2,b)与点D关于原点对称,
∴点D(﹣3,1);
(2)如图所示:
四边形ADBC的面积为:.
20.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)∵点N(﹣3,2),且直线MN∥y轴,
∴m﹣1=﹣3,
解得 m=﹣2.
∴M(﹣3,﹣1),
∴MN=2﹣(﹣1)=3.
21.解:(1)∵点P在x轴上,
∴2+a=0,∴a=﹣2,
∴﹣3a﹣4=2,∴P(2,0)
(2)∵Q(5,8),且PQ∥y轴,
∴﹣3a﹣4=5,a=﹣3,
∴2+a=﹣1,
P(5,﹣1)
22.解:(1)点A(﹣2,3)关于x轴的对称点B的坐标是(﹣2,﹣3),
故把点B向右平移3个单位长度得到点C的坐标是(1,﹣3);
(2)∵点P(0,m)在y轴负半轴上,
∴m<0,
∴﹣m>0,﹣m+1>1,
∴M(﹣m,﹣m+1)落在第一象限.
23.解:A(﹣3,2),B(﹣2,﹣1),C(1,﹣3),D(3,0),E(2,3).
24.解:如图所示:景山(0,1.5),王府井(3,﹣1),天安门(0,﹣2),
中国国家博物馆(1,﹣3),前门(0,﹣5.5),人民大会堂(﹣1,﹣3),
电报大楼(﹣4,﹣2).
25.解:(1)如图所示:
(2)点C1的坐标为:(4,3).
26.解:(1)△ABC的面积是:3×5=7.5;
(2)作图如下:
∴点C′的坐标为:(1,1).
一、选择题(本大题共10小题,每小题2分,共20分).
1.已知点P(2,m)在x轴上,则m的值是( )
A.2 B.0 C.﹣2 D.1
2.在平面直角坐标系中,点(﹣2,﹣3)到x轴的距离是( )
A.﹣2 B.﹣3 C.2 D.3
3.在平面直角坐标系中,下列各点在第三象限的是( )
A.(1,2) B.(﹣2,1) C.(2,﹣1) D.(﹣1,﹣2)
4.棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图是局象棋残局,若在中国象棋盘上建立平面直角坐标系,使表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示“炮”的点的坐标为( )
A.(1,3) B.(3,1) C.(2,3) D.(1,2)
5.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3) B.(1,﹣3) C.(9,8) D.(﹣9,﹣8)
6.若点(a,b)在第四象限,则( )
A.a>b B.a≥b C.a<b D.无法判定 a,b 之间的大小
7.在直角坐标平面内,已知点B和点A(3,4)关于x轴对称,那么点B的坐标( )
A.(3,4) B.(﹣3,﹣4) C.(3,﹣4) D.(﹣3,4)
8.下列语句正确的是( )
A.平行于x轴的直线上所有点的横坐标都相同
B.(﹣3,5)与(5,﹣3)表示两个不同的点
C.若点P(a,b)在y轴上,则b=0
D.若点P(﹣3,4),则P到x轴的距离为3
9.如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为(4,2),四号暗堡的坐标为(﹣2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( )
A.A处 B.B处 C.C处 D.D处
10.点(﹣7,0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
二、填空题(本大题共8小题,每小题2分,共16分.)
11.在直角坐标系中,已知点P的坐标为(﹣3,﹣1),则点P在第 象限.
12.若点P(2m+4,m﹣1)在x轴上,则m= .
13.若点N(a+5,a﹣2)在y轴上,则a= ,N点的坐标为 .
14.如果座位表上“6列3行”记作(6,3),那么(4,3)表示 .
15.在平面直角坐标系中,点P(4,2)关于x轴的对称点的坐标是 .
16.已知点A(m,n)在第四象限,那么点B(m,﹣n)在第 象限.
17.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为 .
18.如图是标准围棋盘的一部分,棋盘上有三枚黑子A,B,C.若棋子A所处位置的坐标为(﹣1,8),棋子B所处位置的坐标为(﹣4,3),则棋子C所处位置的坐标为 .
三、解答题(本大题共8小题,共64分.)
19.已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次联结点A、D、B、C,求所得图形的面积.
20.在平面直角坐标系中,已知点M(m﹣1,2m+3).
(1)若点M在y轴上,求m的值.
(2)若点N(﹣3,2),且直线MN∥y轴,求线段MN的长.
21.已知点P(﹣3a﹣4,2+a),解答下列各题:
(1)若点P在x轴上,试求出点P的坐标;
(2)若Q(5,8),且PQ∥y轴,试求出点P的坐标.
22.(1)在直角坐标系中,将点A(﹣2,3)关于x轴的对称点B向右平移3个单位长度得到点C,求C点的坐标.
(2)已知点P(0,m)在y轴负半轴上,试判断M(﹣m,﹣m+1)落在第几象限.
23.如图,在所给的平面直角坐标系中,写出点A、B、C、D、E的坐标.
24.如图是天安门广场周围的主要景点分布示意图.在此图中建立平面直角坐标系,表示故宫的点坐标为(0,﹣1),表示美术馆的点的坐标为(2,2),并写出其余各景点的坐标.
25.如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标.
26.如图,在直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位,再向右平移5个单位得到△A′B′C′,并写出C′的坐标.
答案
一、选择题
B.D.D.A.A.A.C.B.B.B.
二、填空题
11.三.
12.1.
13.﹣5;(0,﹣7).
14.4列3行.
15.(4,﹣2).
16.一.
17.(3,240°).
18.(2,1).
三、解答题
19.解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,
∴2b+1=﹣1,3a﹣1=2,
解得a=1,b=﹣1,
∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),
∵点C(a+2,b)与点D关于原点对称,
∴点D(﹣3,1);
(2)如图所示:
四边形ADBC的面积为:.
20.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)∵点N(﹣3,2),且直线MN∥y轴,
∴m﹣1=﹣3,
解得 m=﹣2.
∴M(﹣3,﹣1),
∴MN=2﹣(﹣1)=3.
21.解:(1)∵点P在x轴上,
∴2+a=0,∴a=﹣2,
∴﹣3a﹣4=2,∴P(2,0)
(2)∵Q(5,8),且PQ∥y轴,
∴﹣3a﹣4=5,a=﹣3,
∴2+a=﹣1,
P(5,﹣1)
22.解:(1)点A(﹣2,3)关于x轴的对称点B的坐标是(﹣2,﹣3),
故把点B向右平移3个单位长度得到点C的坐标是(1,﹣3);
(2)∵点P(0,m)在y轴负半轴上,
∴m<0,
∴﹣m>0,﹣m+1>1,
∴M(﹣m,﹣m+1)落在第一象限.
23.解:A(﹣3,2),B(﹣2,﹣1),C(1,﹣3),D(3,0),E(2,3).
24.解:如图所示:景山(0,1.5),王府井(3,﹣1),天安门(0,﹣2),
中国国家博物馆(1,﹣3),前门(0,﹣5.5),人民大会堂(﹣1,﹣3),
电报大楼(﹣4,﹣2).
25.解:(1)如图所示:
(2)点C1的坐标为:(4,3).
26.解:(1)△ABC的面积是:3×5=7.5;
(2)作图如下:
∴点C′的坐标为:(1,1).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
