苏科版八年级数学上册第6章一次函数单元测试卷(含答案)
文档属性
| 名称 | 苏科版八年级数学上册第6章一次函数单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 11:03:09 | ||
图片预览




文档简介
第6章一次函数单元测试卷
一、选择题(本大题共10小题,每小题3分,共30分).
1.函数y=2中自变量x的取值范围是( )
A.x≥2 B.x C.x D.x
2.已知点A(﹣2,y1),B(﹣3,y2),C(3,y3)都在关于x的一次函数y=﹣2x+b的图象上,则y1,y2,y3之间的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2<y1<y3 D.y3<y1<y2
3.在平面直角坐标系中,若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度后恰好经过点(﹣1,﹣2),则n的值为( )
A.10 B.8 C.5 D.3
4.若点A(﹣3,y1),B(1,y2)都在直线yx+b上,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2
C.y1>y2 D.无法比较大小
5.按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
6.如图,D2020次哈尔滨至幸福镇的动车需要匀速通过一条隧道(隧道长大于火车长),火车在隧道内的长度与火车进入隧道的时间x之间的关系用图象描述大致是( )
A. B.
C. D.
7.定义运算“※”为a※b,如1※(﹣2)=1×(﹣2)=﹣2,则函数y=2※x的图象大致是( )
A. B.
C. D.
8.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为( )
A.y=2x﹣10 B.y=﹣2x+14 C.y=2x+2 D.yx+5
9.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时30min.小东骑自行车以300m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示,下列说法正确的有几个( )
①家与图书馆之间的路程为4000m;
②小玲步行的速度为100m/min;
③两人出发以后8分钟相遇;
④两人出发以后2min、15mim、20min时相距3000m.
A.1 B.2 C.3 D.4
10.如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(﹣1,0)和B(3,0)两点,则不等式组的解集为( )
A.﹣1<x<3 B.0<x<3 C.﹣1<x<0 D.x>3或x<﹣1
二、填空题(本大题共8小题,每小题2分,共16分.)
11.直线yx+3与两坐标轴围成的三角形的面积为 .
12.点(a,b)在直线y=﹣2x+3上,则4a+2b﹣1= .
13.已知直线l1:y=x+a与直线l2:y=2x+b交于点P(m,4),则代数式ab的值为 .
14.如图,平面直角坐标系中,经过点B(﹣4,0)的直线y=kx+b与直线y=mx+2相交于点A(﹣2,﹣1),则不等式mx+2<kx+b<0的解集为 .
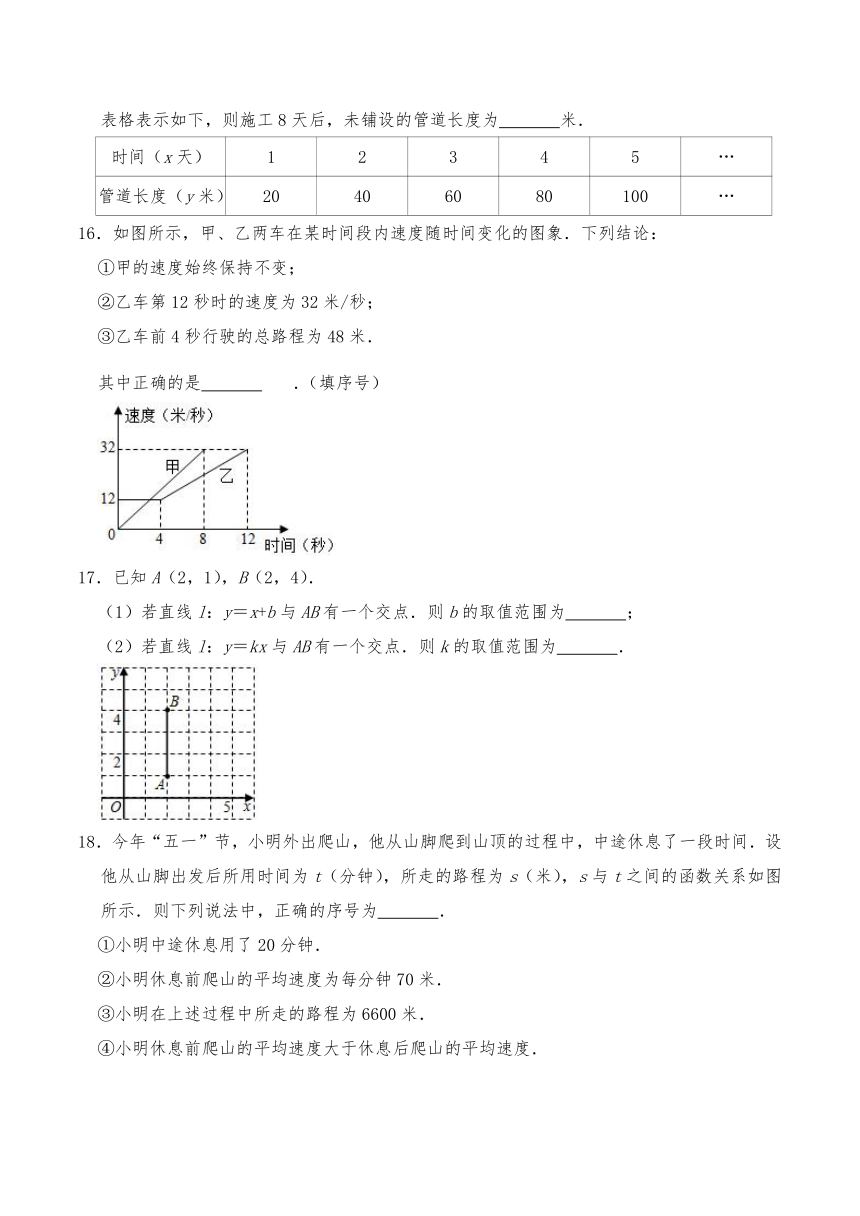
15.农村“雨污分流”工程是“美丽乡村”战略的重要组成部分,我县某村要铺设一条全长为1000米的“雨污分流”管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 米.
时间(x天) 1 2 3 4 5 …
管道长度(y米) 20 40 60 80 100 …
16.如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;
②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.
其中正确的是 .(填序号)
17.已知A(2,1),B(2,4).
(1)若直线l:y=x+b与AB有一个交点.则b的取值范围为 ;
(2)若直线l:y=kx与AB有一个交点.则k的取值范围为 .
18.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为 .
①小明中途休息用了20分钟.
②小明休息前爬山的平均速度为每分钟70米.
③小明在上述过程中所走的路程为6600米.
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
三.解答题(共64分)
19.已知y﹣1与x成正比例,且x=2时,y=7.
(1)求y与x的函数关系式;
(2)当x时,求y的值.
20.在平面直角坐标系xOy中,一次函数y=kx+b的图象与直线y=3x平行,且经过点A(1,6).
(1)求一次函数y=kx+b的解析式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
21.在如图所示的平面直角坐标系中,函数y1=2x+4的图象于x、y轴交于A、B两点,
(1)画出函数y1=2x+4的图象;并求出△AOB的面积;
(2)函数y1=2x+4的图象向上平移1个单位长度得到y2.请直接写出:当y2<0时,x的取值范围.
22.端午小长假,小王一家开车去麦积山景区游玩,返程时从景区出发,其行驶路程s(千米)与时间t(小时)之间的关系如图所示.行驶一段时间到达C地时,汽车突发故障,需停车检修.为了能在高速公路恢复收费前下高速,车修好后加快了速度,结果恰好赶在24时前下高速.结合图中信息,解答下列问题:
(1)上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.
(2)汽车从景区到C地用了几小时?平均每小时行驶多少千米?
(3)车修好后每小时行驶多少千米?
23.某单位要印刷一批宣传材料,在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元;一次印刷页数超过20时,超过部分每页收费0.09元.设该单位需要印刷宣传材料的页数为x(x>20,且x为整数),在甲印刷厂实际付费为y1(元),在乙印刷厂实际付费为y2(元).
(1)分别求出y1,y2与x的函数关系式.
(2)你认为选择哪家印刷厂印刷这批宣传材料较好,为什么?
24.为迎接“国家级文明卫生城市”检查,我市环卫局准备购买A,B两种型号的垃圾箱.通过市场调研发现:购买1个A型垃圾箱和2个B型垃圾箱共需340元;购买3个A型垃圾箱和2个B型垃圾箱共需540元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中购买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费ω(元)与A型垃圾箱x(个)之间的函数关系式;
②当购买A型垃圾箱个数多少时总费用最少,最少费用是多少?
25.如图,是一种斜持包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) … 4 6 8 10 …
双层部分的长度y(cm) … 73 72 71 70 …
(1)求出y关于x的函数解析式,并求当x=150时y的值;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
26.如图所示,已知点M(1,4),N(5,2),P(0,3),Q(3,0),过P,Q两点的直线的函数表达式为y=﹣x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为ts.
(1)若直线PQ随点P向上平移,则:
①当t=3时,求直线PQ的函数表达式.
②当点M,N位于直线PQ的异侧时,确定t的取值范围.
(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.
(3)若点P向上移动,点Q不动.若过点P,Q的直线经过点A(x0,y0),则x0,y0需满足什么条件?请直接写出结论.
答案
一、选择题
B.D.A.A.B.A.A.A.C.A.
二、填空题
11.9.
12.5.
13.2.
14.﹣4<x<﹣2.
15.840.
16.②③.
17.﹣1≤b≤2. k≤2.
18.①②④
三.解答题
19.(1)根据题意设:y﹣1=kx,
把x=2,y=7代入得:6=2k,
解得:k=3,
则y﹣1=3x,即y=3x+1;
(2)把x代入得:y=3×()+1=﹣1+1=0.
20.(1)∵函数y=kx+b的图象与直线y=3x平行,
∴k=3,
又∵函数y=3x+b的图象经过点A(1,6),
∴6=3+b,
解得b=3,
∴一次函数的解析式为y=3x+3;
(2)在y=3x+3中,令x=0,则y=3;令y=0,则x=﹣1;
∴一次函数y=kx+b的图象与坐标轴交于(0,3)和(﹣1,0),
∴一次函数y=kx+b的图象与坐标轴围成的三角形的面积为 1×3.
21.(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示
∵A(﹣2,0)B(0,4),
∴OA=2,OB=4,
∴S△AOB2×4=4;
(2)函数y1=2x+4的图象向上平移1个单位长度得到y2=2x+5,则图象与x轴交于(,0),
根据一次函数的性质则当y2<0时,x的取值范围是.
22.(1)路程与时间之间的关系.自变量是时间,因变量是路程;
(2)由图象可知,汽车从景区到C地用了3小时,速度为:150÷3=50千米/小时;
(3)检修了1小时,修后的速度为75千米/小时.
23.(1)由题意得,y1=0.1x,y2=20×0.12+0.09(x﹣20)=0.09x+0.6,
∴y1,y2与x的函数关系式分别为y1=0.1x,y2=0.09x+0.6;
(2)当x>20时,
由y1<y2得,0.1x<0.09x+0.6,解得,x<60,
由y1=y2得,0.1x=0.09x+0.6,解得,x=60,
由y1>y2得 0.1x>0.09x+0.6,解得,x>60,
∴当x=60时,甲、乙两个印刷厂收费相同,当20<x<60时,甲印刷厂费用少,当x>60时,乙印刷厂费用少.
24.(1)设每个A型垃圾箱x元,每个B型垃圾箱y元,
由题意得:.
解得:.
答:每个A型垃圾箱100元,每个B型垃圾箱120元;
(2)①设购买x个A型垃圾箱,则购买(30﹣x)个B型垃圾箱,
由题意得:ω=100x+120(30﹣x)=﹣20x+3600(0≤x≤16,且x为整数).
②由①知,∵ω=﹣20x+3600,
∴ω是x的一次函数.
∵k=﹣20<0,
∴ω随x的增大而减小.
又0≤x≤16,且x为整数,
∴当x=16,ω取最小值,且最小值为﹣20×16+3600=3280.
答:①函数关系式为ω=﹣20x+3600(0≤x≤16,且x为整数).
②购买16个A型垃圾箱,总费用最少,最少费用为3280元.
25.(1)观察表格可知,y是x的一次函数,设y=kx+b,
则有,
解得,
∴yx+75,
当x=150时,y=0,
答:y关于x的函数解析式为yx+75,当x=150时y的值为0;
(2)由题意,
解得,
所以单层部分的长度为90cm;
(3)由题意得l=x+y=xx+75x+75,
因为0≤x≤150,
所以75x+75≤150,
即75≤l≤150.
26.(1)①设平移后的函数表达式为:y=﹣x+b,其中b=3+t,
故y=﹣x+3+t,
当t=3时,PQ的表达式为:y=﹣x+6;
②当直线PQ过点M时,将点M的坐标代入y=﹣x+3+t得:4=﹣1+3+t,解得:t=2;
同理当直线PQ过点N时,t=4,
故t的取值范围为:2<t<4;
(2)作点N关于y轴的对称轴N′(﹣5,2),连接MN′交y轴于点P,则点P为所求点,
则PN=PN′,
△PMN的周长=MN+PM+PN=MN+PM+PN′=MN+MN′为最小,
设直线MN′的表达式为:y=kx+b,则,解得:,
故直线MN′的表达式为:yx,
当x=0时,y,故点P(0,),
∴t3;
(3)点A(x0,y0),点Q(3,0),点P(0,t+3)
由题意得:x0<3时,y0>﹣x+3,当x0>3时,y0<﹣x0+3.
一、选择题(本大题共10小题,每小题3分,共30分).
1.函数y=2中自变量x的取值范围是( )
A.x≥2 B.x C.x D.x
2.已知点A(﹣2,y1),B(﹣3,y2),C(3,y3)都在关于x的一次函数y=﹣2x+b的图象上,则y1,y2,y3之间的大小关系是( )
A.y1>y2>y3 B.y1<y2<y3 C.y2<y1<y3 D.y3<y1<y2
3.在平面直角坐标系中,若将一次函数y=﹣2x+6的图象向下平移n(n>0)个单位长度后恰好经过点(﹣1,﹣2),则n的值为( )
A.10 B.8 C.5 D.3
4.若点A(﹣3,y1),B(1,y2)都在直线yx+b上,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2
C.y1>y2 D.无法比较大小
5.按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
6.如图,D2020次哈尔滨至幸福镇的动车需要匀速通过一条隧道(隧道长大于火车长),火车在隧道内的长度与火车进入隧道的时间x之间的关系用图象描述大致是( )
A. B.
C. D.
7.定义运算“※”为a※b,如1※(﹣2)=1×(﹣2)=﹣2,则函数y=2※x的图象大致是( )
A. B.
C. D.
8.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为( )
A.y=2x﹣10 B.y=﹣2x+14 C.y=2x+2 D.yx+5
9.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时30min.小东骑自行车以300m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示,下列说法正确的有几个( )
①家与图书馆之间的路程为4000m;
②小玲步行的速度为100m/min;
③两人出发以后8分钟相遇;
④两人出发以后2min、15mim、20min时相距3000m.
A.1 B.2 C.3 D.4
10.如图,直线y1=k1x+b和直线y2=k2x+b分别与x轴交于A(﹣1,0)和B(3,0)两点,则不等式组的解集为( )
A.﹣1<x<3 B.0<x<3 C.﹣1<x<0 D.x>3或x<﹣1
二、填空题(本大题共8小题,每小题2分,共16分.)
11.直线yx+3与两坐标轴围成的三角形的面积为 .
12.点(a,b)在直线y=﹣2x+3上,则4a+2b﹣1= .
13.已知直线l1:y=x+a与直线l2:y=2x+b交于点P(m,4),则代数式ab的值为 .
14.如图,平面直角坐标系中,经过点B(﹣4,0)的直线y=kx+b与直线y=mx+2相交于点A(﹣2,﹣1),则不等式mx+2<kx+b<0的解集为 .
15.农村“雨污分流”工程是“美丽乡村”战略的重要组成部分,我县某村要铺设一条全长为1000米的“雨污分流”管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为 米.
时间(x天) 1 2 3 4 5 …
管道长度(y米) 20 40 60 80 100 …
16.如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;
②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.
其中正确的是 .(填序号)
17.已知A(2,1),B(2,4).
(1)若直线l:y=x+b与AB有一个交点.则b的取值范围为 ;
(2)若直线l:y=kx与AB有一个交点.则k的取值范围为 .
18.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为 .
①小明中途休息用了20分钟.
②小明休息前爬山的平均速度为每分钟70米.
③小明在上述过程中所走的路程为6600米.
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
三.解答题(共64分)
19.已知y﹣1与x成正比例,且x=2时,y=7.
(1)求y与x的函数关系式;
(2)当x时,求y的值.
20.在平面直角坐标系xOy中,一次函数y=kx+b的图象与直线y=3x平行,且经过点A(1,6).
(1)求一次函数y=kx+b的解析式;
(2)求一次函数y=kx+b的图象与坐标轴围成的三角形的面积.
21.在如图所示的平面直角坐标系中,函数y1=2x+4的图象于x、y轴交于A、B两点,
(1)画出函数y1=2x+4的图象;并求出△AOB的面积;
(2)函数y1=2x+4的图象向上平移1个单位长度得到y2.请直接写出:当y2<0时,x的取值范围.
22.端午小长假,小王一家开车去麦积山景区游玩,返程时从景区出发,其行驶路程s(千米)与时间t(小时)之间的关系如图所示.行驶一段时间到达C地时,汽车突发故障,需停车检修.为了能在高速公路恢复收费前下高速,车修好后加快了速度,结果恰好赶在24时前下高速.结合图中信息,解答下列问题:
(1)上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.
(2)汽车从景区到C地用了几小时?平均每小时行驶多少千米?
(3)车修好后每小时行驶多少千米?
23.某单位要印刷一批宣传材料,在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元;一次印刷页数超过20时,超过部分每页收费0.09元.设该单位需要印刷宣传材料的页数为x(x>20,且x为整数),在甲印刷厂实际付费为y1(元),在乙印刷厂实际付费为y2(元).
(1)分别求出y1,y2与x的函数关系式.
(2)你认为选择哪家印刷厂印刷这批宣传材料较好,为什么?
24.为迎接“国家级文明卫生城市”检查,我市环卫局准备购买A,B两种型号的垃圾箱.通过市场调研发现:购买1个A型垃圾箱和2个B型垃圾箱共需340元;购买3个A型垃圾箱和2个B型垃圾箱共需540元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中购买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费ω(元)与A型垃圾箱x(个)之间的函数关系式;
②当购买A型垃圾箱个数多少时总费用最少,最少费用是多少?
25.如图,是一种斜持包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) … 4 6 8 10 …
双层部分的长度y(cm) … 73 72 71 70 …
(1)求出y关于x的函数解析式,并求当x=150时y的值;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
26.如图所示,已知点M(1,4),N(5,2),P(0,3),Q(3,0),过P,Q两点的直线的函数表达式为y=﹣x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为ts.
(1)若直线PQ随点P向上平移,则:
①当t=3时,求直线PQ的函数表达式.
②当点M,N位于直线PQ的异侧时,确定t的取值范围.
(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.
(3)若点P向上移动,点Q不动.若过点P,Q的直线经过点A(x0,y0),则x0,y0需满足什么条件?请直接写出结论.
答案
一、选择题
B.D.A.A.B.A.A.A.C.A.
二、填空题
11.9.
12.5.
13.2.
14.﹣4<x<﹣2.
15.840.
16.②③.
17.﹣1≤b≤2. k≤2.
18.①②④
三.解答题
19.(1)根据题意设:y﹣1=kx,
把x=2,y=7代入得:6=2k,
解得:k=3,
则y﹣1=3x,即y=3x+1;
(2)把x代入得:y=3×()+1=﹣1+1=0.
20.(1)∵函数y=kx+b的图象与直线y=3x平行,
∴k=3,
又∵函数y=3x+b的图象经过点A(1,6),
∴6=3+b,
解得b=3,
∴一次函数的解析式为y=3x+3;
(2)在y=3x+3中,令x=0,则y=3;令y=0,则x=﹣1;
∴一次函数y=kx+b的图象与坐标轴交于(0,3)和(﹣1,0),
∴一次函数y=kx+b的图象与坐标轴围成的三角形的面积为 1×3.
21.(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示
∵A(﹣2,0)B(0,4),
∴OA=2,OB=4,
∴S△AOB2×4=4;
(2)函数y1=2x+4的图象向上平移1个单位长度得到y2=2x+5,则图象与x轴交于(,0),
根据一次函数的性质则当y2<0时,x的取值范围是.
22.(1)路程与时间之间的关系.自变量是时间,因变量是路程;
(2)由图象可知,汽车从景区到C地用了3小时,速度为:150÷3=50千米/小时;
(3)检修了1小时,修后的速度为75千米/小时.
23.(1)由题意得,y1=0.1x,y2=20×0.12+0.09(x﹣20)=0.09x+0.6,
∴y1,y2与x的函数关系式分别为y1=0.1x,y2=0.09x+0.6;
(2)当x>20时,
由y1<y2得,0.1x<0.09x+0.6,解得,x<60,
由y1=y2得,0.1x=0.09x+0.6,解得,x=60,
由y1>y2得 0.1x>0.09x+0.6,解得,x>60,
∴当x=60时,甲、乙两个印刷厂收费相同,当20<x<60时,甲印刷厂费用少,当x>60时,乙印刷厂费用少.
24.(1)设每个A型垃圾箱x元,每个B型垃圾箱y元,
由题意得:.
解得:.
答:每个A型垃圾箱100元,每个B型垃圾箱120元;
(2)①设购买x个A型垃圾箱,则购买(30﹣x)个B型垃圾箱,
由题意得:ω=100x+120(30﹣x)=﹣20x+3600(0≤x≤16,且x为整数).
②由①知,∵ω=﹣20x+3600,
∴ω是x的一次函数.
∵k=﹣20<0,
∴ω随x的增大而减小.
又0≤x≤16,且x为整数,
∴当x=16,ω取最小值,且最小值为﹣20×16+3600=3280.
答:①函数关系式为ω=﹣20x+3600(0≤x≤16,且x为整数).
②购买16个A型垃圾箱,总费用最少,最少费用为3280元.
25.(1)观察表格可知,y是x的一次函数,设y=kx+b,
则有,
解得,
∴yx+75,
当x=150时,y=0,
答:y关于x的函数解析式为yx+75,当x=150时y的值为0;
(2)由题意,
解得,
所以单层部分的长度为90cm;
(3)由题意得l=x+y=xx+75x+75,
因为0≤x≤150,
所以75x+75≤150,
即75≤l≤150.
26.(1)①设平移后的函数表达式为:y=﹣x+b,其中b=3+t,
故y=﹣x+3+t,
当t=3时,PQ的表达式为:y=﹣x+6;
②当直线PQ过点M时,将点M的坐标代入y=﹣x+3+t得:4=﹣1+3+t,解得:t=2;
同理当直线PQ过点N时,t=4,
故t的取值范围为:2<t<4;
(2)作点N关于y轴的对称轴N′(﹣5,2),连接MN′交y轴于点P,则点P为所求点,
则PN=PN′,
△PMN的周长=MN+PM+PN=MN+PM+PN′=MN+MN′为最小,
设直线MN′的表达式为:y=kx+b,则,解得:,
故直线MN′的表达式为:yx,
当x=0时,y,故点P(0,),
∴t3;
(3)点A(x0,y0),点Q(3,0),点P(0,t+3)
由题意得:x0<3时,y0>﹣x+3,当x0>3时,y0<﹣x0+3.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
