青岛版八年级下册数学10.5一次函数与一元一次不等式(共18张PPT)
文档属性
| 名称 | 青岛版八年级下册数学10.5一次函数与一元一次不等式(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 272.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 11:20:08 | ||
图片预览




文档简介
(共18张PPT)
第10章 一次函数
10.5 一次函数与一元一次不等式
通过观察一次函数的图象,体会一次函数与一元一次不等式的关系;
会运用图象法求一元一次不等式的解集.感悟数形结合、转化的数学思想.
学习目标
温故知新
直线y=kx+b的图象与y轴交点的坐标为________.与x轴交点的坐标为_________.
(0,b)
(- ,0)
直线y=2x+4的图象与y轴交点的坐标为________.与x轴交点的坐标为_________.
(0,4)
(- 2,0)
一元一次方程2x+4=0的解为______.即直线y=2x+2与___轴交点的___坐标
x=-2
x
横
新课探究
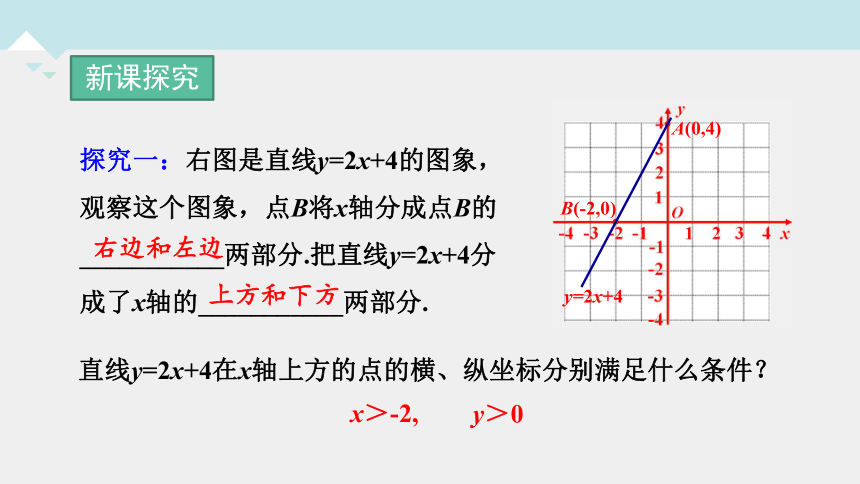
探究一:右图是直线y=2x+4的图象,观察这个图象,点B将x轴分成点B的___________两部分.把直线y=2x+4分成了x轴的___________两部分.
y=2x+4
A(0,4)
B(-2,0)
右边和左边
上方和下方
直线y=2x+4在x轴上方的点的横、纵坐标分别满足什么条件?
y>0
x>-2,
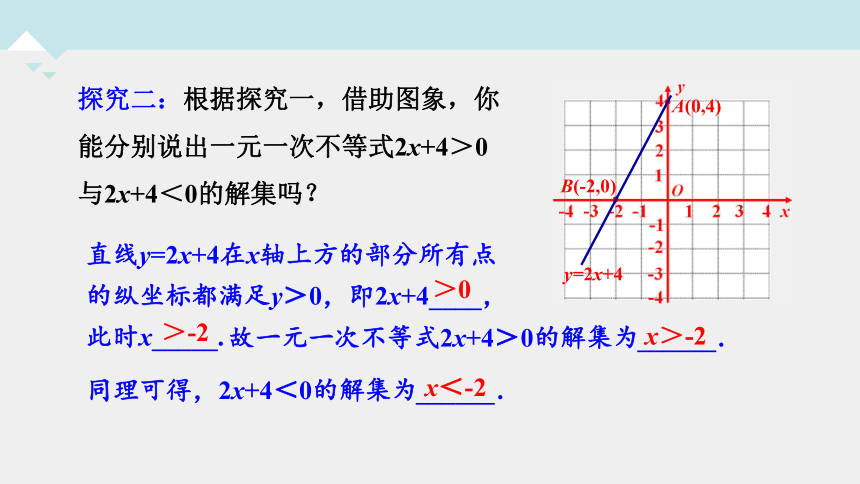
探究二:根据探究一,借助图象,你能分别说出一元一次不等式2x+4>0与2x+4<0的解集吗?
y=2x+4
A(0,4)
B(-2,0)
直线y=2x+4在x轴上方的部分所有点的纵坐标都满足y>0,即2x+4____,此时x_____.
故一元一次不等式2x+4>0的解集为______.
同理可得,2x+4<0的解集为______.
>-2
>0
x>-2
x<-2
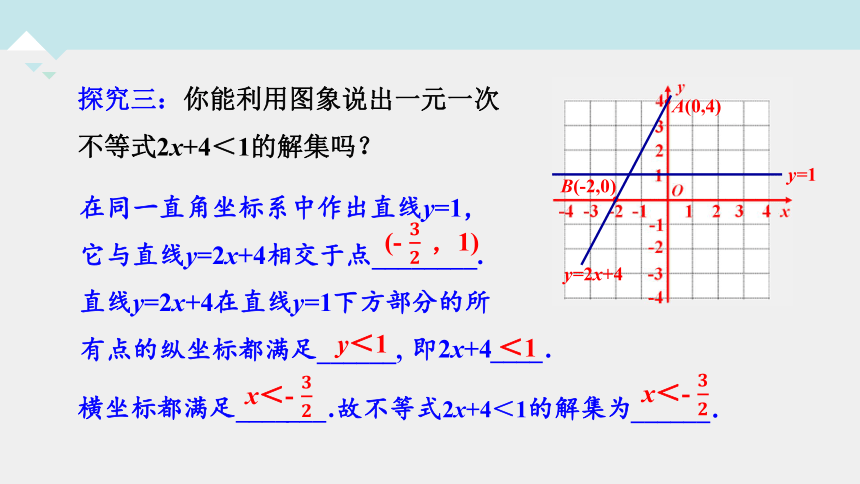
探究三:你能利用图象说出一元一次不等式2x+4<1的解集吗?
y=2x+4
A(0,4)
B(-2,0)
在同一直角坐标系中作出直线y=1,
它与直线y=2x+4相交于点________.
直线y=2x+4在直线y=1下方部分的所有点的纵坐标都满足______,
(- ,1)
y=1
y<1
即2x+4____.
<1
横坐标都满足_______.
x<-
故不等式2x+4<1的解集为______.
x<-
在同一直角坐标系中作出直线y= c和直线y= ax+b,相交于点__________.
当a>0时,不等式ax+b>c的解集是________,
探究四:由探究二、探究三你能总结出利用图象求一元一次不等式ax+b>c或ax+b<c的解集的方法吗?
( ,c)
x>
当a<0时,不等式ax+b>c的解集是______,不等式ax+b<c的解集是______.
不等式ax+b<c的解集是______;
x<
x<
x>
归纳总结一:
任何一个一元一次不等式都可变形转化为kx+b>0或kx+b<0(k,b为常数,k≠0)的形式.
一元一次不等式kx+b>0(或kx+b<0)的解集,就是使一次函数y= kx+b的函数值大于0(或小于0)时自变量x的取值范围,即直线y= kx+b位于x轴上方(或下方)的部分对应的x的取值范围.
【例1】如图是一次函数y1 =-x+2与y2 =3x-3在同一直角坐标系中的图象,利用图象说明:当x取何值时,y1=y2?当x取何值时,y1>y2 ?当x取何值时,y1<y2 ?
解:先求出两个图象交点的坐标.令y1=y2,即-x+2=3x-3.
解得 x= .此时, y1=y2= .
y2=3x-3
y1=-x+2
因此,两直线交点的坐标为(,).
即当x=时, y1=y2=.
由图象还可以看出,当x<时,直线y1 在直线y2的上方,此时y1 >y2.当x>时,直线y1在直线y2的下方,此时y1y2=3x-3
y1=-x+2
【例2】你能利用一次函数的图象,分别求出一元一次不等式-x+2>3x-3和-x+2<3x-3的解集吗?说明你的想法.
思路点拨:令y1=-x+2, y2=3x-3,在同一直角坐标系中分别画出这两个函数的图象.
y2=3x-3
y1=-x+2
至此,我们发现这个题就是求例1中的y1>y2和y1归纳总结二:
求关于x的不等式k1x+b1>k2x+b2或k1x+b1<k2x+b2的解集时,
可分别令y1=k1x+b1,y2=k2x+b2,在同一直角坐标系中分别画出两个一次函数的图象,先令k1x+b1=k2x+b2 ,找出两个函数图象交点的横坐标,然后根据图象的位置确定不等式的解集.
课堂练习
1.当x取何值时,函数y=2x+6的值满足以下条件?
(1) y=0 (2)y>0
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
5
6
y=2x+6
解:先画出函数y=2x+6的图象.
由图象可知,当x=-3时,y=0;当x>-3时,y>0.
2.利用图象解不等式:5x-1 >2x+5
y2=2x+5
解:令y1= 5x-1, y2=2x+5 ,在同一直角坐标系中分别画出这两个函数的图象.
令y1=y2,即5x-1=2x+5,得x=2.
结合图象,得不等式5x-1>2x+5的解为x>2.
y1= 5x-1
3.已知函数y=2x-1.当x取何值时,y>1?x>y?y>x+1?
解法一:要使y>1 ,只需2x-1>1,解得x>1.
所以,当x>1时, y>1.
要使x>y ,只需x>2x-1,解得x<1.
所以,当x<1时,x>y .
要使y>x+1 ,只需2x-1>x+1 ,解得x>2.
所以,当x>2时,y>x+1 .
解法二:令y2=x, y3=x+1,在同一直角坐标系中分别画出这三个函数的图象.
y2=x
y= 2x-1
y3=x+1
由图象可以看出:
当x>1时, y>1.
当x<1时,x>y .
当x>2时,y>x+1 .
3.已知函数y=2x-1.当x取何值时,y>1?x>y?y>x+1?
课堂小结
如何借助一次函数解一元一次不等式?
图象位于x轴上方(或下方)的部分对应的x的取值范围.
解kx+b>0(或kx+b<0)
y= kx+b
y>0(或y<0)
解一元一次不等式
变形转化
谢谢!
第10章 一次函数
10.5 一次函数与一元一次不等式
通过观察一次函数的图象,体会一次函数与一元一次不等式的关系;
会运用图象法求一元一次不等式的解集.感悟数形结合、转化的数学思想.
学习目标
温故知新
直线y=kx+b的图象与y轴交点的坐标为________.与x轴交点的坐标为_________.
(0,b)
(- ,0)
直线y=2x+4的图象与y轴交点的坐标为________.与x轴交点的坐标为_________.
(0,4)
(- 2,0)
一元一次方程2x+4=0的解为______.即直线y=2x+2与___轴交点的___坐标
x=-2
x
横
新课探究
探究一:右图是直线y=2x+4的图象,观察这个图象,点B将x轴分成点B的___________两部分.把直线y=2x+4分成了x轴的___________两部分.
y=2x+4
A(0,4)
B(-2,0)
右边和左边
上方和下方
直线y=2x+4在x轴上方的点的横、纵坐标分别满足什么条件?
y>0
x>-2,
探究二:根据探究一,借助图象,你能分别说出一元一次不等式2x+4>0与2x+4<0的解集吗?
y=2x+4
A(0,4)
B(-2,0)
直线y=2x+4在x轴上方的部分所有点的纵坐标都满足y>0,即2x+4____,此时x_____.
故一元一次不等式2x+4>0的解集为______.
同理可得,2x+4<0的解集为______.
>-2
>0
x>-2
x<-2
探究三:你能利用图象说出一元一次不等式2x+4<1的解集吗?
y=2x+4
A(0,4)
B(-2,0)
在同一直角坐标系中作出直线y=1,
它与直线y=2x+4相交于点________.
直线y=2x+4在直线y=1下方部分的所有点的纵坐标都满足______,
(- ,1)
y=1
y<1
即2x+4____.
<1
横坐标都满足_______.
x<-
故不等式2x+4<1的解集为______.
x<-
在同一直角坐标系中作出直线y= c和直线y= ax+b,相交于点__________.
当a>0时,不等式ax+b>c的解集是________,
探究四:由探究二、探究三你能总结出利用图象求一元一次不等式ax+b>c或ax+b<c的解集的方法吗?
( ,c)
x>
当a<0时,不等式ax+b>c的解集是______,不等式ax+b<c的解集是______.
不等式ax+b<c的解集是______;
x<
x<
x>
归纳总结一:
任何一个一元一次不等式都可变形转化为kx+b>0或kx+b<0(k,b为常数,k≠0)的形式.
一元一次不等式kx+b>0(或kx+b<0)的解集,就是使一次函数y= kx+b的函数值大于0(或小于0)时自变量x的取值范围,即直线y= kx+b位于x轴上方(或下方)的部分对应的x的取值范围.
【例1】如图是一次函数y1 =-x+2与y2 =3x-3在同一直角坐标系中的图象,利用图象说明:当x取何值时,y1=y2?当x取何值时,y1>y2 ?当x取何值时,y1<y2 ?
解:先求出两个图象交点的坐标.令y1=y2,即-x+2=3x-3.
解得 x= .此时, y1=y2= .
y2=3x-3
y1=-x+2
因此,两直线交点的坐标为(,).
即当x=时, y1=y2=.
由图象还可以看出,当x<时,直线y1 在直线y2的上方,此时y1 >y2.当x>时,直线y1在直线y2的下方,此时y1
y1=-x+2
【例2】你能利用一次函数的图象,分别求出一元一次不等式-x+2>3x-3和-x+2<3x-3的解集吗?说明你的想法.
思路点拨:令y1=-x+2, y2=3x-3,在同一直角坐标系中分别画出这两个函数的图象.
y2=3x-3
y1=-x+2
至此,我们发现这个题就是求例1中的y1>y2和y1
求关于x的不等式k1x+b1>k2x+b2或k1x+b1<k2x+b2的解集时,
可分别令y1=k1x+b1,y2=k2x+b2,在同一直角坐标系中分别画出两个一次函数的图象,先令k1x+b1=k2x+b2 ,找出两个函数图象交点的横坐标,然后根据图象的位置确定不等式的解集.
课堂练习
1.当x取何值时,函数y=2x+6的值满足以下条件?
(1) y=0 (2)y>0
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
5
6
y=2x+6
解:先画出函数y=2x+6的图象.
由图象可知,当x=-3时,y=0;当x>-3时,y>0.
2.利用图象解不等式:5x-1 >2x+5
y2=2x+5
解:令y1= 5x-1, y2=2x+5 ,在同一直角坐标系中分别画出这两个函数的图象.
令y1=y2,即5x-1=2x+5,得x=2.
结合图象,得不等式5x-1>2x+5的解为x>2.
y1= 5x-1
3.已知函数y=2x-1.当x取何值时,y>1?x>y?y>x+1?
解法一:要使y>1 ,只需2x-1>1,解得x>1.
所以,当x>1时, y>1.
要使x>y ,只需x>2x-1,解得x<1.
所以,当x<1时,x>y .
要使y>x+1 ,只需2x-1>x+1 ,解得x>2.
所以,当x>2时,y>x+1 .
解法二:令y2=x, y3=x+1,在同一直角坐标系中分别画出这三个函数的图象.
y2=x
y= 2x-1
y3=x+1
由图象可以看出:
当x>1时, y>1.
当x<1时,x>y .
当x>2时,y>x+1 .
3.已知函数y=2x-1.当x取何值时,y>1?x>y?y>x+1?
课堂小结
如何借助一次函数解一元一次不等式?
图象位于x轴上方(或下方)的部分对应的x的取值范围.
解kx+b>0(或kx+b<0)
y= kx+b
y>0(或y<0)
解一元一次不等式
变形转化
谢谢!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
