(青岛版)六年级上册数学 第五单元第2课时圆的周长(课件)(共37张PPT)
文档属性
| 名称 | (青岛版)六年级上册数学 第五单元第2课时圆的周长(课件)(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
5.2合作探索:圆的周长
青岛版六年级数学上册素养达标课件
核心素养
在具体情境中,结合已有的知识经验认识什么是圆的周长。
通过测量和计算,了解圆的周长与直径的比为定值,推出圆的周长公式。
运用圆的周长公式公式解决现实问题。
01
02
03
引导学生在活动中探索圆的周长计算方法。
对圆周率的正确理解。
在观察、实验、猜想、验证等活动中,养成发展转化策略和推理能力。
课时目标
知识链接,感受文化素养。
学习任务一
知识回顾
计算下面图形的周长。
=(5+2)×2=14(cm)
=4×3=12(cm)
知识链接
你能提出什么问题?
知识链接
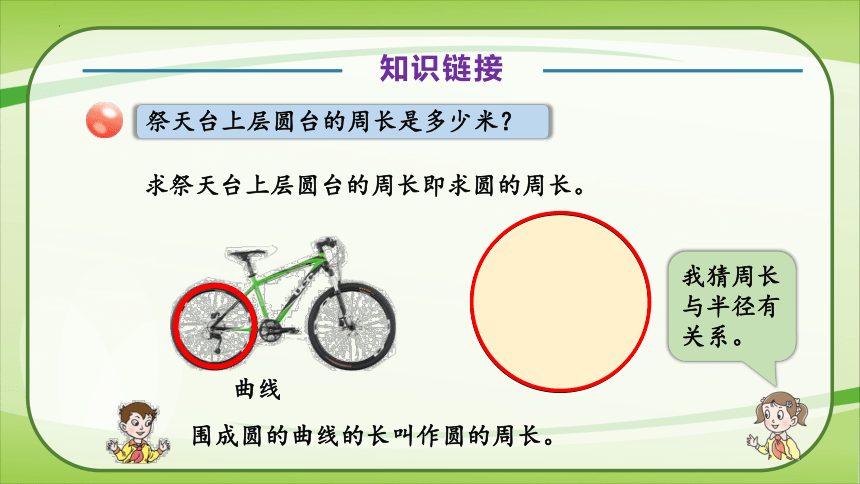
祭天台上层圆台的周长是多少米?
求祭天台上层圆台的周长即求圆的周长。
曲线
围成圆的曲线的长叫作圆的周长。
我猜周长与半径有关系。
知识链接
测量几个圆的直径和周长,看它们有什么关系。
绕线法:用线绕圆片一周,量线的长度。
0
1
2
3
4
6
7
8
5
知识链接
滚动法:
圆片向右滚动一周,量它的长度。
0
1
2
3
4
6
7
8
5
2厘米
测量发现:大小不同的圆的周长是不同的,而圆的大小由直径(或半径)决定的,因此圆的周长与直径(或半径)之间一定存在着某种关系。
知识链接
圆的周长与直径之间有什么关系?
圆的周长除以直径的商(结果保留两位小数)
圆的周长
圆的直径
圆的周长是直径的3倍多一些(或3倍左右)。
9.4 cm
3 cm
12.55 cm
4 cm
6.3 cm
2 cm
15.7 cm
5 cm
3.15
3.13
3.14
3.14
知识链接
由于我们在测量时存在一定的误差,计算出的圆周长与直径的比值可能不完全相同,但实际上这个比值是一个固定不变的数,这个比值叫作圆周率,用希腊字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,π≈3.14。
圆的周长÷直径=π
圆的周长=π×直径
如果用字母C 表示0圆的周长,就得到C =πd 。
再根据直径与半径的关系,得到 C=2πr。
知识链接
祭天台上层圆台的周长是多少米?
3.14×30 = 94.2(米)=
求祭天台上层圆台的周长是多少米,就是已知直径求圆的周长。C =πd
答:祭天台上层圆台的周长是94.2米。
学习任务二
新知构建,完善核心素养。
学习活动
祈年殿殿顶的直径是多少米?
方法一:
解:设祈年殿殿顶的直径是x米。
x×3.14=100
x×3.14÷3.14=100÷3.14
x ≈ 31.85
C =πd = 2πr
d = C÷π r = C÷π÷2
答:祈年殿殿顶的直径约是31.85米。
学习活动
祈年殿殿顶的直径是多少米?
方法二:
100÷3.14≈ 31.85(米)
C =πd = 2πr
d = C÷π r = C÷π÷2
计算除不尽时,得数一般保留两位小数。
学习活动
圆的周长和它的直径的比值是一个固定的数,这个比值就叫作圆周率,用字母π表示。
圆周率是一个无限不循环小数:π=3.1415926535…,在实际应用中,一般取它的近似值,即π≈ 3.14。
学习任务三
学以致用,检验目标达成。
学习活动
1. 求下面各圆的周长。
2×3.14×3=18.84(cm)
3.14×6=18.84(cm)
2×3.14×5=31.4(cm)
规范解答:
学习活动
2. 右图是古代人们用来磨面的石碾。如果石碾的半径是1.2米,估一估,绕石碾走一圈大约是多少米?
学习活动
3.时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
2×3.14×12
=6.28×12
=75.36(厘米)
2×3.14×18
=6.28×18
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
分针走一小时,它的尖端走过的路程是113.04厘米。
学习活动
4.请将表格补充完整。(单位:米)
4
12.56
4.5
28.26
6
3
学习活动
5. 一元硬币的周长是 7.85 厘米。这个储钱罐能否放进一元的硬币?
学习活动
6.火眼金睛辨对错。
(1)圆规两脚间的距离是4厘米,画出的圆的周长是12.56厘米。
( )
(2)圆的周长与它直径的比的比值是 π。 ( )
(3)两圆半径的比是2∶1,则其周长的比是4∶1。 ( )
(4)半圆的周长就是圆周长的一半。 ( )
×
√
×
×
学习活动
7. 以车轮直径的大小而论,目前世界上能骑行的双轮自行车车轮直径最大的为 3.05 米,最小的为 1.9 厘米;最小的独轮自行车的车轮直径为 1.3 厘米。
(1)最大的双轮自行车车轮转一周大约前进多少米?(得数保留一位小数)
(2)车轮转动一周,最小的双轮自行车比独轮自行车大约多行多少厘米?(得数保留整数)
学习活动
(3)你还能提出什么问题?
学习活动
8.依墙而建的鸡舍围成半圆形,其直径为5米。
(1)需要多长的篱笆?
(2)如果将鸡舍的直径增加2米,需要增
加多长的篱笆?
(1)3.14×5÷2=7.85(米)
答:需要7.85米的篱笆。
(2)方法一:3.14×(5+2)÷2-7.85=3.14(米)
方法二:3.14×2÷2=3.14(米)
答:需要增加3.14米的篱笆。
学习活动
9.(1)用 20 米的铁丝制作像右图这样的铁环,最多能制作多少个?
(2)如果铁环的直径是 35 厘米,要制作 20 个铁环,至少需要多少米的铁丝?
10. 圆形水池四周种了 40 棵树,每两棵树之间的距离是 1.57 米。这个水池的半径是多少米?
学习活动
11.右面是一个国际标准田径跑道的示意图。跑道的一周是多少米?
73×3.14+85.39×2
=229.22 +170.78
=400(米)
答:跑道的一周是400米。
学习活动
12. 装卸工人把 4 根圆柱形钢管用铁丝捆扎在一起(如右图)。钢管的横截面直径是 10 厘米,如果铁丝接头处的长度忽略不计,捆扎 2 圈,需要多长的铁丝?
学习总结
今天你学会了什么?
你是怎么学会的?
素养评价
自我评价
内容 评价等级
A B C
学习态度
学习自信
学习合作
小组互评
内容 评价等级
A B C
学习态度
学习自信
学习合作
5.2合作探索:圆的周长
青岛版六年级数学上册素养达标课件
核心素养
在具体情境中,结合已有的知识经验认识什么是圆的周长。
通过测量和计算,了解圆的周长与直径的比为定值,推出圆的周长公式。
运用圆的周长公式公式解决现实问题。
01
02
03
引导学生在活动中探索圆的周长计算方法。
对圆周率的正确理解。
在观察、实验、猜想、验证等活动中,养成发展转化策略和推理能力。
课时目标
知识链接,感受文化素养。
学习任务一
知识回顾
计算下面图形的周长。
=(5+2)×2=14(cm)
=4×3=12(cm)
知识链接
你能提出什么问题?
知识链接
祭天台上层圆台的周长是多少米?
求祭天台上层圆台的周长即求圆的周长。
曲线
围成圆的曲线的长叫作圆的周长。
我猜周长与半径有关系。
知识链接
测量几个圆的直径和周长,看它们有什么关系。
绕线法:用线绕圆片一周,量线的长度。
0
1
2
3
4
6
7
8
5
知识链接
滚动法:
圆片向右滚动一周,量它的长度。
0
1
2
3
4
6
7
8
5
2厘米
测量发现:大小不同的圆的周长是不同的,而圆的大小由直径(或半径)决定的,因此圆的周长与直径(或半径)之间一定存在着某种关系。
知识链接
圆的周长与直径之间有什么关系?
圆的周长除以直径的商(结果保留两位小数)
圆的周长
圆的直径
圆的周长是直径的3倍多一些(或3倍左右)。
9.4 cm
3 cm
12.55 cm
4 cm
6.3 cm
2 cm
15.7 cm
5 cm
3.15
3.13
3.14
3.14
知识链接
由于我们在测量时存在一定的误差,计算出的圆周长与直径的比值可能不完全相同,但实际上这个比值是一个固定不变的数,这个比值叫作圆周率,用希腊字母π表示。它是一个无限不循环小数,π=3.1415926535……但在实际应用中常常只取它的近似值,π≈3.14。
圆的周长÷直径=π
圆的周长=π×直径
如果用字母C 表示0圆的周长,就得到C =πd 。
再根据直径与半径的关系,得到 C=2πr。
知识链接
祭天台上层圆台的周长是多少米?
3.14×30 = 94.2(米)=
求祭天台上层圆台的周长是多少米,就是已知直径求圆的周长。C =πd
答:祭天台上层圆台的周长是94.2米。
学习任务二
新知构建,完善核心素养。
学习活动
祈年殿殿顶的直径是多少米?
方法一:
解:设祈年殿殿顶的直径是x米。
x×3.14=100
x×3.14÷3.14=100÷3.14
x ≈ 31.85
C =πd = 2πr
d = C÷π r = C÷π÷2
答:祈年殿殿顶的直径约是31.85米。
学习活动
祈年殿殿顶的直径是多少米?
方法二:
100÷3.14≈ 31.85(米)
C =πd = 2πr
d = C÷π r = C÷π÷2
计算除不尽时,得数一般保留两位小数。
学习活动
圆的周长和它的直径的比值是一个固定的数,这个比值就叫作圆周率,用字母π表示。
圆周率是一个无限不循环小数:π=3.1415926535…,在实际应用中,一般取它的近似值,即π≈ 3.14。
学习任务三
学以致用,检验目标达成。
学习活动
1. 求下面各圆的周长。
2×3.14×3=18.84(cm)
3.14×6=18.84(cm)
2×3.14×5=31.4(cm)
规范解答:
学习活动
2. 右图是古代人们用来磨面的石碾。如果石碾的半径是1.2米,估一估,绕石碾走一圈大约是多少米?
学习活动
3.时针长12厘米,如果走一圈,它的尖端走过的路程是多少?分针长18厘米,如果走1小时,它的尖端走过的路程是多少?
2×3.14×12
=6.28×12
=75.36(厘米)
2×3.14×18
=6.28×18
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
分针走一小时,它的尖端走过的路程是113.04厘米。
学习活动
4.请将表格补充完整。(单位:米)
4
12.56
4.5
28.26
6
3
学习活动
5. 一元硬币的周长是 7.85 厘米。这个储钱罐能否放进一元的硬币?
学习活动
6.火眼金睛辨对错。
(1)圆规两脚间的距离是4厘米,画出的圆的周长是12.56厘米。
( )
(2)圆的周长与它直径的比的比值是 π。 ( )
(3)两圆半径的比是2∶1,则其周长的比是4∶1。 ( )
(4)半圆的周长就是圆周长的一半。 ( )
×
√
×
×
学习活动
7. 以车轮直径的大小而论,目前世界上能骑行的双轮自行车车轮直径最大的为 3.05 米,最小的为 1.9 厘米;最小的独轮自行车的车轮直径为 1.3 厘米。
(1)最大的双轮自行车车轮转一周大约前进多少米?(得数保留一位小数)
(2)车轮转动一周,最小的双轮自行车比独轮自行车大约多行多少厘米?(得数保留整数)
学习活动
(3)你还能提出什么问题?
学习活动
8.依墙而建的鸡舍围成半圆形,其直径为5米。
(1)需要多长的篱笆?
(2)如果将鸡舍的直径增加2米,需要增
加多长的篱笆?
(1)3.14×5÷2=7.85(米)
答:需要7.85米的篱笆。
(2)方法一:3.14×(5+2)÷2-7.85=3.14(米)
方法二:3.14×2÷2=3.14(米)
答:需要增加3.14米的篱笆。
学习活动
9.(1)用 20 米的铁丝制作像右图这样的铁环,最多能制作多少个?
(2)如果铁环的直径是 35 厘米,要制作 20 个铁环,至少需要多少米的铁丝?
10. 圆形水池四周种了 40 棵树,每两棵树之间的距离是 1.57 米。这个水池的半径是多少米?
学习活动
11.右面是一个国际标准田径跑道的示意图。跑道的一周是多少米?
73×3.14+85.39×2
=229.22 +170.78
=400(米)
答:跑道的一周是400米。
学习活动
12. 装卸工人把 4 根圆柱形钢管用铁丝捆扎在一起(如右图)。钢管的横截面直径是 10 厘米,如果铁丝接头处的长度忽略不计,捆扎 2 圈,需要多长的铁丝?
学习总结
今天你学会了什么?
你是怎么学会的?
素养评价
自我评价
内容 评价等级
A B C
学习态度
学习自信
学习合作
小组互评
内容 评价等级
A B C
学习态度
学习自信
学习合作
