2023-2024学年 人教版数学八年级数学下册 勾股定理的证明 课件(共28张PPT)
文档属性
| 名称 | 2023-2024学年 人教版数学八年级数学下册 勾股定理的证明 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 787.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 00:00:00 | ||
图片预览


文档简介
(共28张PPT)
勾股定理的证明
2023-2024学年人教版数学八年级下册 第17章 勾股定理
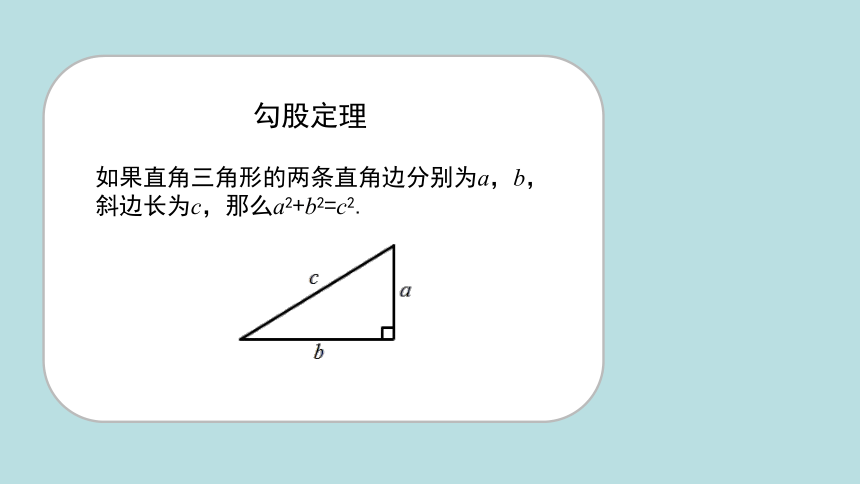
勾股定理
如果直角三角形的两条直角边分别为a,b,斜边长为c,那么a2+b2=c2.
勾股定理是平面几何中一个极为重
的不同人士曾先后给出数百种证明.
要的定理,历史上不同时代、不同国别
尤其出色.
其中,我国古代对这个定理的证明
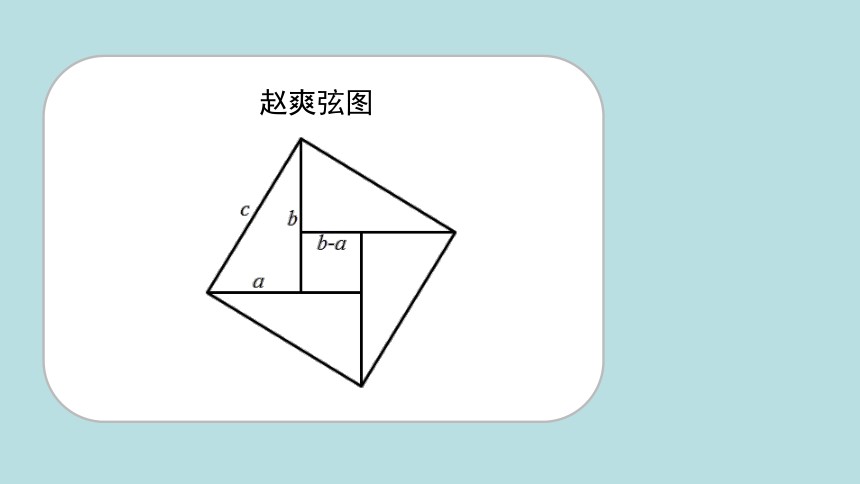
赵爽弦图
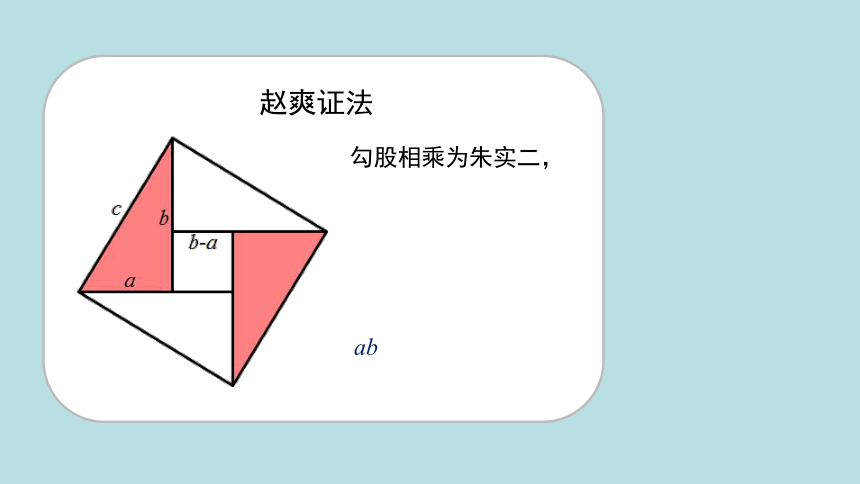
赵爽证法
勾股相乘为朱实二,
ab
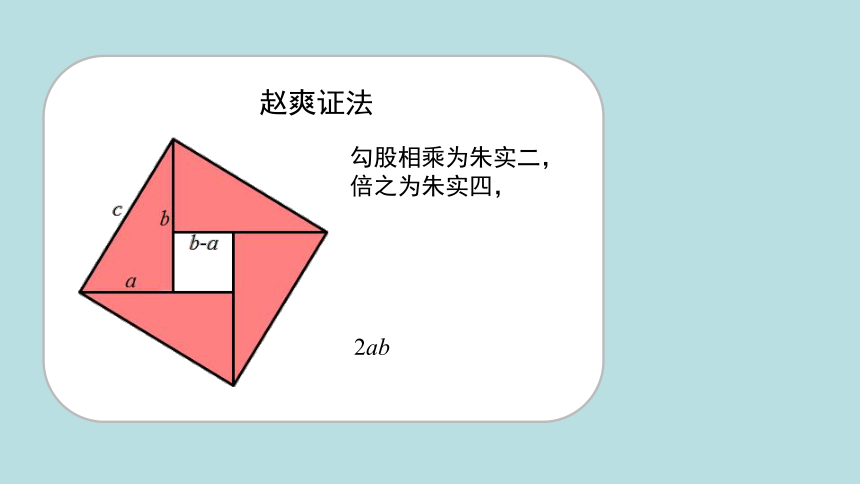
赵爽证法
勾股相乘为朱实二,倍之为朱实四,
2ab
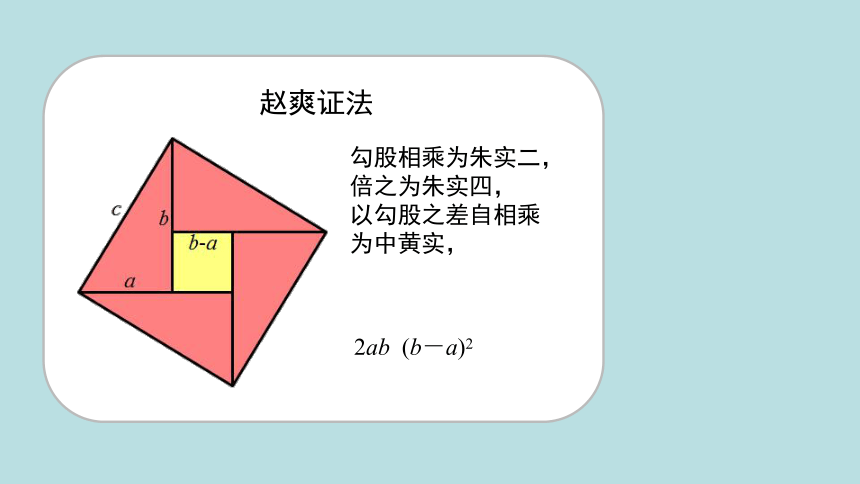
赵爽证法
勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实,
2ab (b-a)2
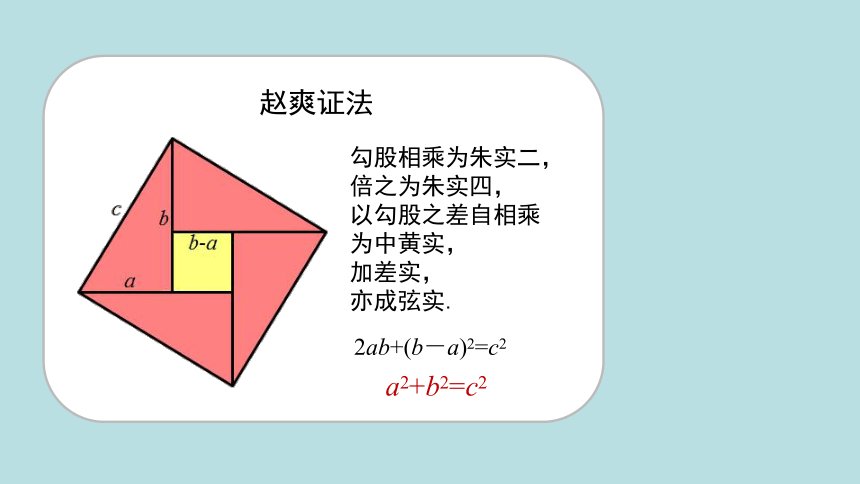
赵爽证法
勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实,
加差实,
亦成弦实.
2ab+(b-a)2=c2
a2+b2=c2
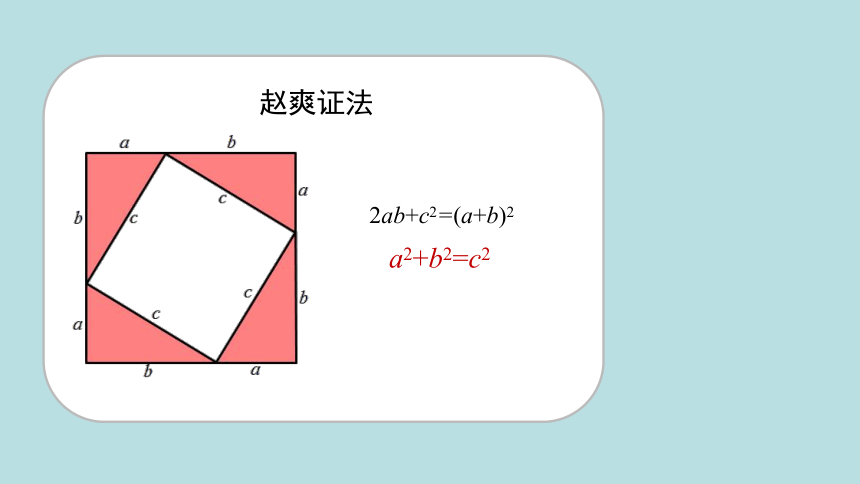
赵爽证法
2ab+c2=(a+b)2
a2+b2=c2
赵爽证法
2ab+c2=(a+b)2
a2+b2=c2
总统证法(J.A.Garfield)
a2+b2=c2
赵爽证法
赵爽证法
a2+b2=c2
项名达证法
a2+b2=c2
刘徽证法
刘徽证法
朱出
大青出
小青出
朱入
大青入
小青入
a2+b2=c2
出入相补,各从其类.
达芬奇证法中国改良版
达芬奇证法中国改良版
达芬奇证法中国改良版
a2+b2=c2
欧几里得证法(Bride's Chair)
欧几里得证法
欧几里得证法
a2+b2=c2
赵爽弦图
勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实,
加差实,
亦成弦实.
“弦图”这一简洁优美的
证明显示了中国古代数学家的
智慧与成就,经过艺术处理的
弦图作为北京2002年国际数学
家大会的会徽,经各国代表传
扬全球四方.
欧几里得
达芬奇
加菲尔德
刘徽
华蘅芳
赵爽
勾股定理的众多证明方法
倾注着历史上不同民族顶级数
学家的智慧,折射着不同文化
背景下创造性数学思维的光芒,
并且东西易趣,交相辉映.
对于数学来说,整个文明世界就是
一个国家!
——希尔伯特
参考文献:
数学文化小丛书
李大潜 主编
高等教育出版社
再见!
勾股定理的证明
2023-2024学年人教版数学八年级下册 第17章 勾股定理
勾股定理
如果直角三角形的两条直角边分别为a,b,斜边长为c,那么a2+b2=c2.
勾股定理是平面几何中一个极为重
的不同人士曾先后给出数百种证明.
要的定理,历史上不同时代、不同国别
尤其出色.
其中,我国古代对这个定理的证明
赵爽弦图
赵爽证法
勾股相乘为朱实二,
ab
赵爽证法
勾股相乘为朱实二,倍之为朱实四,
2ab
赵爽证法
勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实,
2ab (b-a)2
赵爽证法
勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实,
加差实,
亦成弦实.
2ab+(b-a)2=c2
a2+b2=c2
赵爽证法
2ab+c2=(a+b)2
a2+b2=c2
赵爽证法
2ab+c2=(a+b)2
a2+b2=c2
总统证法(J.A.Garfield)
a2+b2=c2
赵爽证法
赵爽证法
a2+b2=c2
项名达证法
a2+b2=c2
刘徽证法
刘徽证法
朱出
大青出
小青出
朱入
大青入
小青入
a2+b2=c2
出入相补,各从其类.
达芬奇证法中国改良版
达芬奇证法中国改良版
达芬奇证法中国改良版
a2+b2=c2
欧几里得证法(Bride's Chair)
欧几里得证法
欧几里得证法
a2+b2=c2
赵爽弦图
勾股相乘为朱实二,倍之为朱实四,
以勾股之差自相乘为中黄实,
加差实,
亦成弦实.
“弦图”这一简洁优美的
证明显示了中国古代数学家的
智慧与成就,经过艺术处理的
弦图作为北京2002年国际数学
家大会的会徽,经各国代表传
扬全球四方.
欧几里得
达芬奇
加菲尔德
刘徽
华蘅芳
赵爽
勾股定理的众多证明方法
倾注着历史上不同民族顶级数
学家的智慧,折射着不同文化
背景下创造性数学思维的光芒,
并且东西易趣,交相辉映.
对于数学来说,整个文明世界就是
一个国家!
——希尔伯特
参考文献:
数学文化小丛书
李大潜 主编
高等教育出版社
再见!
