6.3 梯形的面积(教学课件)五年级数学上册人教版(共27张PPT)
文档属性
| 名称 | 6.3 梯形的面积(教学课件)五年级数学上册人教版(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-17 00:00:00 | ||
图片预览


文档简介
(共27张PPT)
第六单元 多边形的面积
第三课时
梯形的面积
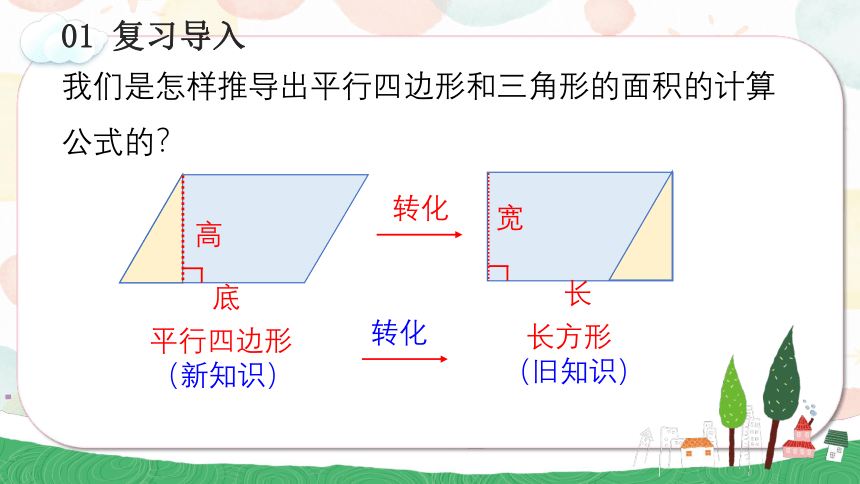
我们是怎样推导出平行四边形和三角形的面积的计算公式的?
平行四边形
(新知识)
长方形
(旧知识)
转化
转化
01 复习导入
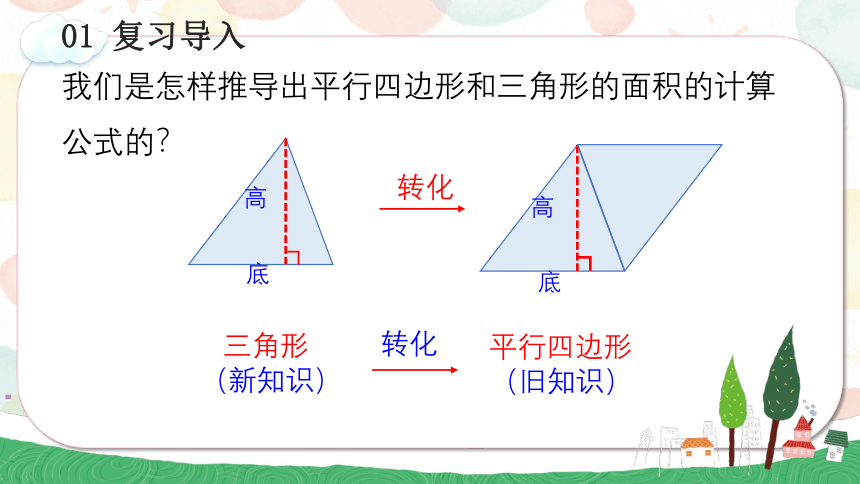
我们是怎样推导出平行四边形和三角形的面积的计算公式的?
高
底
高
底
三角形
(新知识)
平行四边形
(旧知识)
转化
转化
01 复习导入
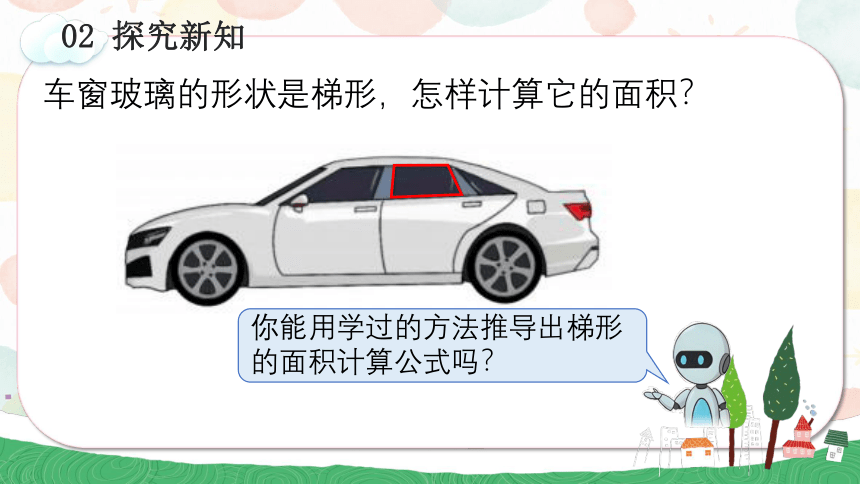
车窗玻璃的形状是梯形,怎样计算它的面积?
你能用学过的方法推导出梯形的面积计算公式吗?
02 探究新知
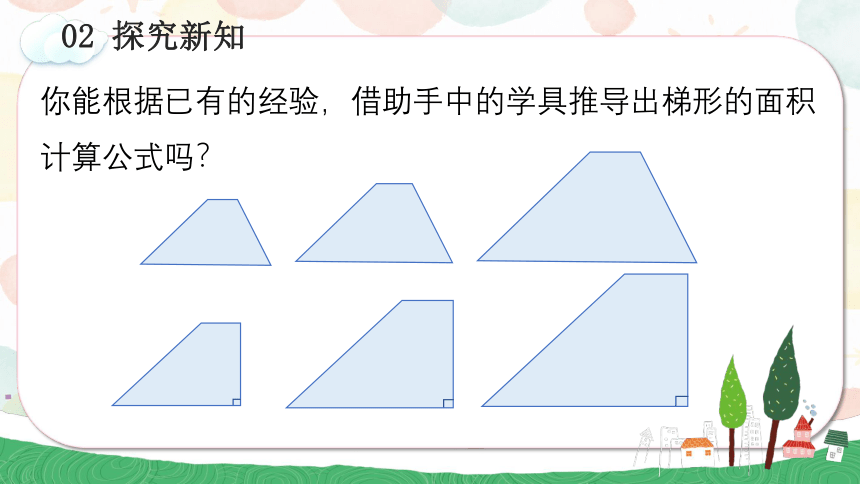
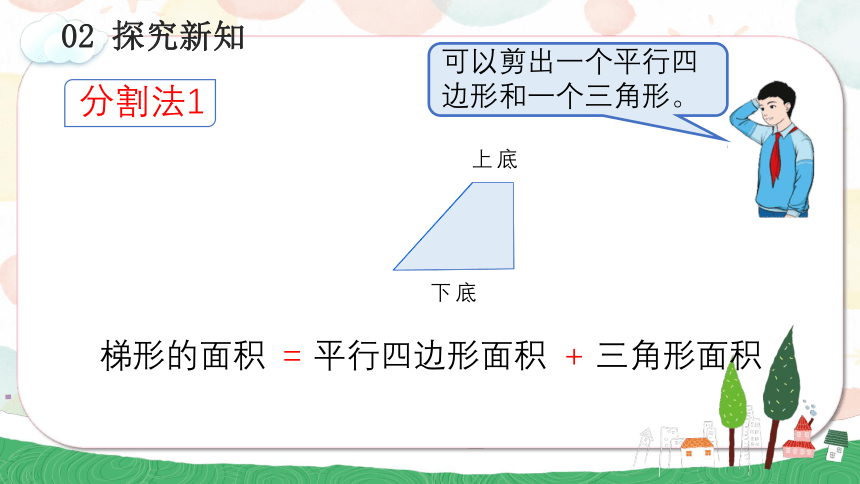
你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?
02 探究新知
下底
上底
梯形的面积
=
平行四边形面积
+
三角形面积
分割法1
02 探究新知
可以剪出一个平行四边形和一个三角形。
梯形的面积
=
平行四边形面积
+
三角形面积
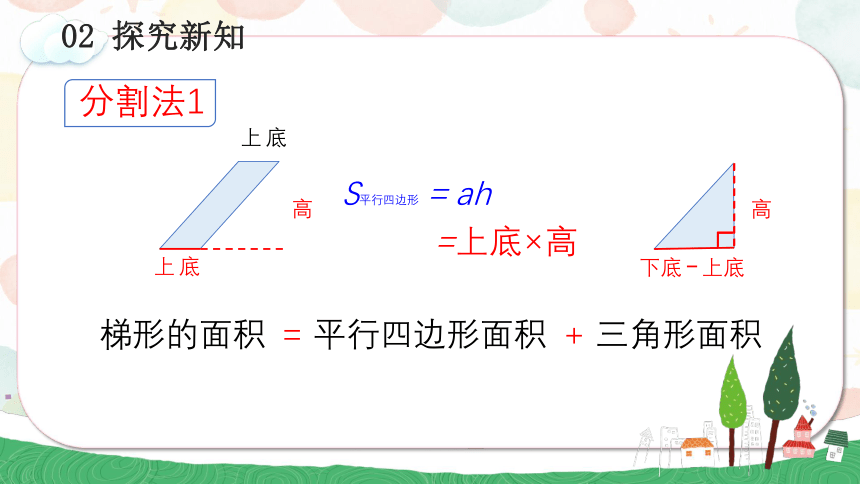
上底
上底
下底 上底
高
高
S平行四边形=ah
=上底×高
02 探究新知
分割法1
梯形的面积
=
平行四边形面积
+
三角形面积
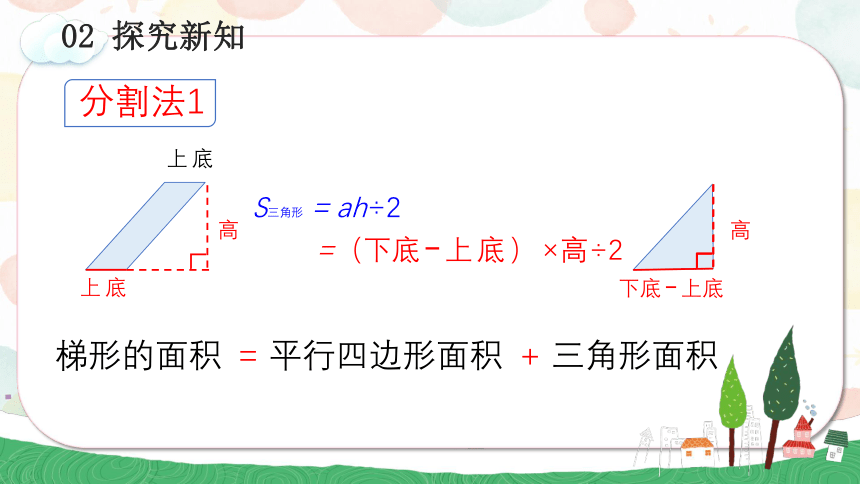
上底
上底
下底 上底
高
高
S三角形=ah÷2
=(下底 上底)×高÷2
02 探究新知
分割法1
梯形的面积
=
平行四边形面积
+
三角形面积
上底×高
+
(下底 上底)×高÷2
=
[上底+(下底 上底)÷2]×高
=
(上底÷2+下底÷2)×高
=
(上底+下底)×高÷2
02 探究新知
梯形的面积
=
A三角形面积
+
B三角形面积
下底
上底
A三角形
B三角形
上底
下底
高
高
02 探究新知
分割法2
我把一个梯形剪成了两个三角形。
A三角形
B三角形
上底
下底
高
高
SA三角形 =ah÷2
=上底×高÷2
梯形的面积
=
A三角形面积
+
B三角形面积
02 探究新知
分割法2
梯形的面积
=
A三角形面积
+
B三角形面积
A三角形
B三角形
上底
下底
高
高
SB三角形=ah÷2
=下底×高÷2
=
上底×高÷2+下底×高÷2
=
(上底+下底)×高÷2
02 探究新知
分割法2
拼接法1
上底
下底
高
上底
下底
+
底边
02 探究新知
两个一样的梯形可以拼成一个平行四边形。
(
)
平行四边形面积
底
高
×
=
相等
相等
相等
2个完全一样的
梯形面积
上底下底的和
高
×
=
梯形的面积
上底
高
×
=
÷
2
上底
下底
高
+
下底
上底
下底
+
底边
02 探究新知
拼接法1
(
)
长方形面积
长
宽
×
=
相等
相等
相等
2个完全一样的
梯形面积
上底下底的和
高
×
=
梯形的面积
上底
高
×
=
÷
2
上底
下底
高
+
下底
上底
下底
+
长
02 探究新知
拼接法2
任意两个完全相同的梯形可以拼成一个平行四边形(长方形或正方形)。
02 探究新知
观察拼成的平行四边形和原来的梯形,你发现了什么
梯形的面积=
(上底+下底)×高÷2
如果用S表示梯形的面积,用a表示梯形的上底,用b表示梯形的下底,用h表示梯形的高,梯形的面积计算公式可以写成:
02 探究新知
S=(a+b)h÷2
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
02 探究新知
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
02 探究新知
S =(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 平方米。
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
03 课堂练习
A
B
SA=(aA+bA) hA÷2
=(40+71)×40÷2
=2220(cm2)
=111×40÷2
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
03 课堂练习
A
B
答:它们的面积分别是2220cm 、2200cm 。
SB=(aB+bB) hB ÷2
=(45+65)×40÷2
=2200(cm2)
=110×40÷2
03 课堂练习
2.一条新挖的水渠,横截面是梯形(如图)。渠口宽2.8m,渠底宽1.4m,渠深1.2m。横截面的面积是多少平方米?
=(1.4 + 2.8)×1.2÷2
=4.2×1.2÷2
= 2.52(m2)
答:它的横截面积是 2.52 m2。
S=(a+b)h÷2
03 课堂练习
3.已知一个梯形的面积是15 cm2 。它的上底是4.5 cm,高是3 cm,下底是多少厘米 ( 列方程解决。)
=15x2÷3-4.5
=5.5(cm2)
答:下底5.5 cm2。
S=(a+b)h÷2
b=Sx2÷h-a
03 课堂练习
04 课堂小结
这节课有什么收获呢?
梯形的面积
S=(a+b)h÷2
梯形的面积=(上底+下底)×高÷2
课后作业
1.完成对应的课时的练习;
2.从课时练中选取。
下课啦
同学们
第六单元 多边形的面积
第三课时
梯形的面积
我们是怎样推导出平行四边形和三角形的面积的计算公式的?
平行四边形
(新知识)
长方形
(旧知识)
转化
转化
01 复习导入
我们是怎样推导出平行四边形和三角形的面积的计算公式的?
高
底
高
底
三角形
(新知识)
平行四边形
(旧知识)
转化
转化
01 复习导入
车窗玻璃的形状是梯形,怎样计算它的面积?
你能用学过的方法推导出梯形的面积计算公式吗?
02 探究新知
你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?
02 探究新知
下底
上底
梯形的面积
=
平行四边形面积
+
三角形面积
分割法1
02 探究新知
可以剪出一个平行四边形和一个三角形。
梯形的面积
=
平行四边形面积
+
三角形面积
上底
上底
下底 上底
高
高
S平行四边形=ah
=上底×高
02 探究新知
分割法1
梯形的面积
=
平行四边形面积
+
三角形面积
上底
上底
下底 上底
高
高
S三角形=ah÷2
=(下底 上底)×高÷2
02 探究新知
分割法1
梯形的面积
=
平行四边形面积
+
三角形面积
上底×高
+
(下底 上底)×高÷2
=
[上底+(下底 上底)÷2]×高
=
(上底÷2+下底÷2)×高
=
(上底+下底)×高÷2
02 探究新知
梯形的面积
=
A三角形面积
+
B三角形面积
下底
上底
A三角形
B三角形
上底
下底
高
高
02 探究新知
分割法2
我把一个梯形剪成了两个三角形。
A三角形
B三角形
上底
下底
高
高
SA三角形 =ah÷2
=上底×高÷2
梯形的面积
=
A三角形面积
+
B三角形面积
02 探究新知
分割法2
梯形的面积
=
A三角形面积
+
B三角形面积
A三角形
B三角形
上底
下底
高
高
SB三角形=ah÷2
=下底×高÷2
=
上底×高÷2+下底×高÷2
=
(上底+下底)×高÷2
02 探究新知
分割法2
拼接法1
上底
下底
高
上底
下底
+
底边
02 探究新知
两个一样的梯形可以拼成一个平行四边形。
(
)
平行四边形面积
底
高
×
=
相等
相等
相等
2个完全一样的
梯形面积
上底下底的和
高
×
=
梯形的面积
上底
高
×
=
÷
2
上底
下底
高
+
下底
上底
下底
+
底边
02 探究新知
拼接法1
(
)
长方形面积
长
宽
×
=
相等
相等
相等
2个完全一样的
梯形面积
上底下底的和
高
×
=
梯形的面积
上底
高
×
=
÷
2
上底
下底
高
+
下底
上底
下底
+
长
02 探究新知
拼接法2
任意两个完全相同的梯形可以拼成一个平行四边形(长方形或正方形)。
02 探究新知
观察拼成的平行四边形和原来的梯形,你发现了什么
梯形的面积=
(上底+下底)×高÷2
如果用S表示梯形的面积,用a表示梯形的上底,用b表示梯形的下底,用h表示梯形的高,梯形的面积计算公式可以写成:
02 探究新知
S=(a+b)h÷2
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
02 探究新知
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
02 探究新知
S =(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 平方米。
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
03 课堂练习
A
B
SA=(aA+bA) hA÷2
=(40+71)×40÷2
=2220(cm2)
=111×40÷2
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
03 课堂练习
A
B
答:它们的面积分别是2220cm 、2200cm 。
SB=(aB+bB) hB ÷2
=(45+65)×40÷2
=2200(cm2)
=110×40÷2
03 课堂练习
2.一条新挖的水渠,横截面是梯形(如图)。渠口宽2.8m,渠底宽1.4m,渠深1.2m。横截面的面积是多少平方米?
=(1.4 + 2.8)×1.2÷2
=4.2×1.2÷2
= 2.52(m2)
答:它的横截面积是 2.52 m2。
S=(a+b)h÷2
03 课堂练习
3.已知一个梯形的面积是15 cm2 。它的上底是4.5 cm,高是3 cm,下底是多少厘米 ( 列方程解决。)
=15x2÷3-4.5
=5.5(cm2)
答:下底5.5 cm2。
S=(a+b)h÷2
b=Sx2÷h-a
03 课堂练习
04 课堂小结
这节课有什么收获呢?
梯形的面积
S=(a+b)h÷2
梯形的面积=(上底+下底)×高÷2
课后作业
1.完成对应的课时的练习;
2.从课时练中选取。
下课啦
同学们
