二元一次方程组实践与探索1(福建省泉州市)
文档属性
| 名称 | 二元一次方程组实践与探索1(福建省泉州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-26 00:00:00 | ||
图片预览






文档简介
课件14张PPT。§7.3实践与探索列二元一次方程组解决实际问题的步骤是什么?
1、设适当的未知数。(注意单位)2、根据题意,寻找两个等量关系。3、根据两个等量关系,列出方程组。4、解方程组。5、检验是否符合题意。6、作答。复习提问(关键)其中什么是关键?
要用20张白卡纸做长方体的包装盒,已知每张白卡纸可以做侧面2个,或者做底面3个.如果1个侧面和2个底面可以做成一个包装盒,那么能否把这些白卡纸分成两部分,一部分做侧面,一部分做底面,使做成的侧面和底面正好配套?
请你设计一种分法. 探索新知课本P31 问题11、本题有哪些已知量?
2、从已知中找出两个等量关系.
3、本题求什么?
4、若设用x张白卡纸做侧面, y张白卡纸做底面,那么可以做侧面多少个?底面多少个?
(1)共有白卡纸20张。
(2)一张白卡纸可以做侧面2个或底面3个。
(3)1个侧面与2个底面配成一套。用几张白卡纸做侧面?几张白卡纸做底面?(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20
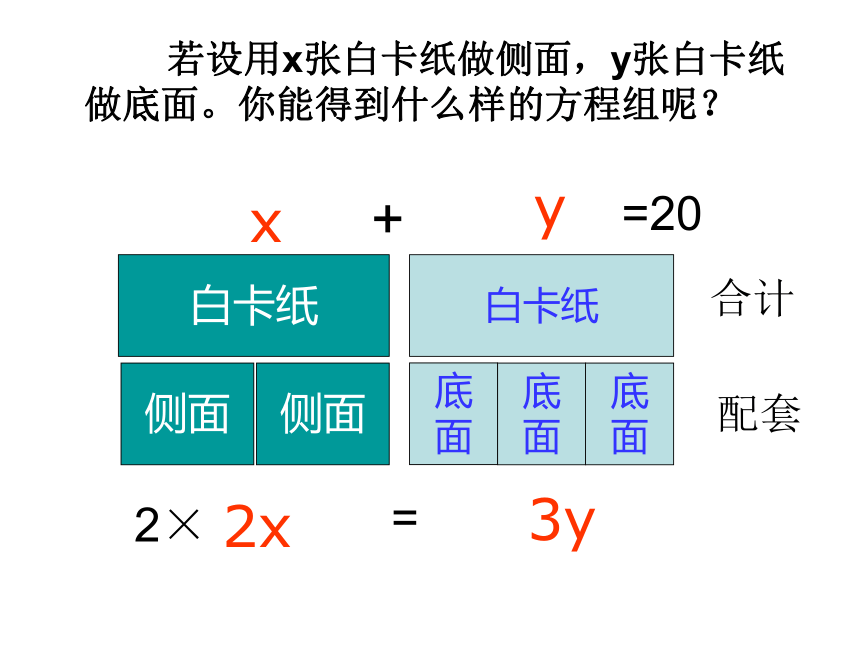
(2)由已知(3)可知:侧面的个数×2=底面的个数分析 抽象 若设用x张白卡纸做侧面,y张白卡纸做底面。你能得到什么样的方程组呢?白卡纸白卡纸侧面底
面侧面底
面底
面2x3yxy解这个方程组,得因为方程组的解为分数,所以若白卡纸不允许剪开,则找不到符合题意的分法.设用x张白卡纸做侧面,y张白卡纸做底面。根据题意,得解:①②如果一张白卡纸可以适当的套裁出一个侧面和一个底面,那么又怎样分这些白卡纸,才能既使做出的侧面和底面配套,又能充分利用白卡纸?若可套裁,
用8张白卡纸做侧面,可做8×2=16(个)
用11张白卡纸做底面,可做11×3=33(个)
余下的1张套裁出1个侧面和1个底面。
共可做侧面17个,底面34个,正好配成17个包装盒,较充分地利用了材料。想一想 一张方桌由一个桌面和四条桌腿组成,假设1立方米木料可制作方桌桌面50个,或制作桌腿300条,现有5立方米木料,那么用多少木料做桌面,用多少木料做桌腿,使得做出的桌面和桌腿正好配套?能配成多少张方桌?练习课本P36第15题若设用x立方米木料做桌面,y立方米木料做桌腿,可列表分析:xy50x300y解:设用χ立方米木料做桌面,y立方米木料做桌腿,依题意得
①②解这个方程组得经检验,符合题意。答:用3立方米木料做桌面,2立方米木料做桌腿,恰好能配 成150张方桌。当χ=3时,50×3=150(张)甲纸盒展开图乙种纸盒展开图某纸品厂利用边角料裁剪出如图一所示的正方形纸片1000张和长方形纸片2000张,正方形的边长与长方形的宽相等。现准备充分利用这些纸片制作如图二的甲、乙两种无盖纸盒,各可做成多少个?x2y4x3y发散10002000解:设能做x只甲种纸盒,y只乙种纸盒,则根据题意,可得解这个方程组,得答:能做200只甲种纸盒,400只乙种纸盒,
恰好把纸板用完。经检验,符合题意。总结实际问题分析抽象方程(组)求解检验问题解决1.这节课你学到了哪些知识和方法?2. 你还有什么问题或想法需要和大家交流?1、某车间每个工人一天能生产螺栓12个或生产螺母18个,每个螺栓要与两个螺母配套,现有工人28人,怎样分配生产螺栓与螺母的工人数才能使每天的生产量刚好配套?
2、一张圆凳由一个凳面和三条腿组成,如果1立方米木料可制作300条凳腿,或制作凳面50个,现有9立方米木料,请你设计一下,用多少木料做凳腿,用多少木料做凳面,做出的凳面和凳腿恰好配套?能配成多少张圆凳?课外作业20张卡纸,20=7×2+6,余数是6,因此和6张相似,可以做4个盒14张纸可以做6×2=12个盒则可以做16个盒子,余下一张纸和一个盒底盖。
要用20张白卡纸做长方体的包装盒,已知每张白卡纸可以做侧面2个,或者做底面3个.如果1个侧面和2个底面可以做成一个包装盒,那么能否把这些白卡纸分成两部分,一部分做侧面,一部分做底面,使做成的侧面和底面正好配套?
请你设计一种分法. 探索新知课本P31 问题11、本题有哪些已知量?
2、从已知中找出两个等量关系.
3、本题求什么?
4、若设用x张白卡纸做侧面, y张白卡纸做底面,那么可以做侧面多少个?底面多少个?
(1)共有白卡纸20张。
(2)一张白卡纸可以做侧面2个或底面3个。
(3)1个侧面与2个底面配成一套。用几张白卡纸做侧面?几张白卡纸做底面?(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20
(2)由已知(3)可知:侧面的个数×2=底面的个数分析 抽象 若设用x张白卡纸做侧面,y张白卡纸做底面。你能得到什么样的方程组呢?白卡纸白卡纸侧面底
面侧面底
面底
面2x3yxy解这个方程组,得因为方程组的解为分数,所以若白卡纸不允许剪开,则找不到符合题意的分法.设用x张白卡纸做侧面,y张白卡纸做底面。根据题意,得解:①②如果一张白卡纸可以适当的套裁出一个侧面和一个底面,那么又怎样分这些白卡纸,才能既使做出的侧面和底面配套,又能充分利用白卡纸?若可套裁,
用8张白卡纸做侧面,可做8×2=16(个)
用11张白卡纸做底面,可做11×3=33(个)
余下的1张套裁出1个侧面和1个底面。
共可做侧面17个,底面34个,正好配成17个包装盒,较充分地利用了材料。想一想 一张方桌由一个桌面和四条桌腿组成,假设1立方米木料可制作方桌桌面50个,或制作桌腿300条,现有5立方米木料,那么用多少木料做桌面,用多少木料做桌腿,使得做出的桌面和桌腿正好配套?能配成多少张方桌?练习课本P36第15题若设用x立方米木料做桌面,y立方米木料做桌腿,可列表分析:xy50x300y解:设用χ立方米木料做桌面,y立方米木料做桌腿,依题意得
①②解这个方程组得经检验,符合题意。答:用3立方米木料做桌面,2立方米木料做桌腿,恰好能配 成150张方桌。当χ=3时,50×3=150(张)甲纸盒展开图乙种纸盒展开图某纸品厂利用边角料裁剪出如图一所示的正方形纸片1000张和长方形纸片2000张,正方形的边长与长方形的宽相等。现准备充分利用这些纸片制作如图二的甲、乙两种无盖纸盒,各可做成多少个?x2y4x3y发散10002000解:设能做x只甲种纸盒,y只乙种纸盒,则根据题意,可得解这个方程组,得答:能做200只甲种纸盒,400只乙种纸盒,
恰好把纸板用完。经检验,符合题意。总结实际问题分析抽象方程(组)求解检验问题解决1.这节课你学到了哪些知识和方法?2. 你还有什么问题或想法需要和大家交流?1、某车间每个工人一天能生产螺栓12个或生产螺母18个,每个螺栓要与两个螺母配套,现有工人28人,怎样分配生产螺栓与螺母的工人数才能使每天的生产量刚好配套?
2、一张圆凳由一个凳面和三条腿组成,如果1立方米木料可制作300条凳腿,或制作凳面50个,现有9立方米木料,请你设计一下,用多少木料做凳腿,用多少木料做凳面,做出的凳面和凳腿恰好配套?能配成多少张圆凳?课外作业20张卡纸,20=7×2+6,余数是6,因此和6张相似,可以做4个盒14张纸可以做6×2=12个盒则可以做16个盒子,余下一张纸和一个盒底盖。
