江苏省无锡市宜兴市丁蜀学区2023-2024学年八年级上学期第一次课堂练习数学试卷(无答案)
文档属性
| 名称 | 江苏省无锡市宜兴市丁蜀学区2023-2024学年八年级上学期第一次课堂练习数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 354.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 15:32:41 | ||
图片预览


文档简介
2023-2024学年第一学期初二年级数学学科
第一次课堂练习试卷
出卷人: 审卷人: 出卷日期: 2023.10
一、单选题(本题共10小题,每小题3分,共30分)
1.下列手机屏幕解锁图形案是轴对称图形的是( )
A. B. C. D.
2.如图,,,,则判定△ABC ≌△ABD 的依据是( )
A. B. C. D.无法确定
3.如图,在△ACD与中,,再添加下列哪个条件,能判定( )
A. B. C.DA平分 D.
4.如图,的面积为垂直于的平分线于点,则的面积为( )
A. B. C. D.
5.如图,在△ABC中,D为线段AB的垂直平分线与BC延长线的交点,连接AD,若AD=7,BC=3,则CD的长为( )
A.3 B.4 C.6 D.7
第2题 第3题 第4题 第5题
如图,在△ABC中,,将△ABC沿着直线l折叠,点C落在点D的位置,则的度数是( )
A. B. C. D.
7.如图,直线AB、CD相交于点O,P为这两条直线外一点,连接OP.点P关于直线AB、CD的对称点分别是点P1、P2.若OP=3.5,则点P1、P2之间的距离可能是( )
A.5 B.9 C.7 D.11
8.如图,在四边形ABCD中,,E为BC的中点,连接DE,AE,,延长DE交AB的延长线于点F.若,则AD的长为( )
A.0 B.6 C.7 D.9
第6题 第7题 第8题
9.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使BPE与CQP全等.
A.1 B.1或4 C.1或2 D.2或4
10.如图,在中,,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①;②;③;④若,则.正确的结论序号是( )
A.①② B.①②④ C.②③④ D.①③④
第9题 第10题
二、填空题(本题共8小题,每小题3分,共24分)
11.已知△ABC△DEF,∠A=50°,∠B=75°,则∠F= .
12.一位球员的球衣号码为,那么他在镜子中看到自己的号码是 .
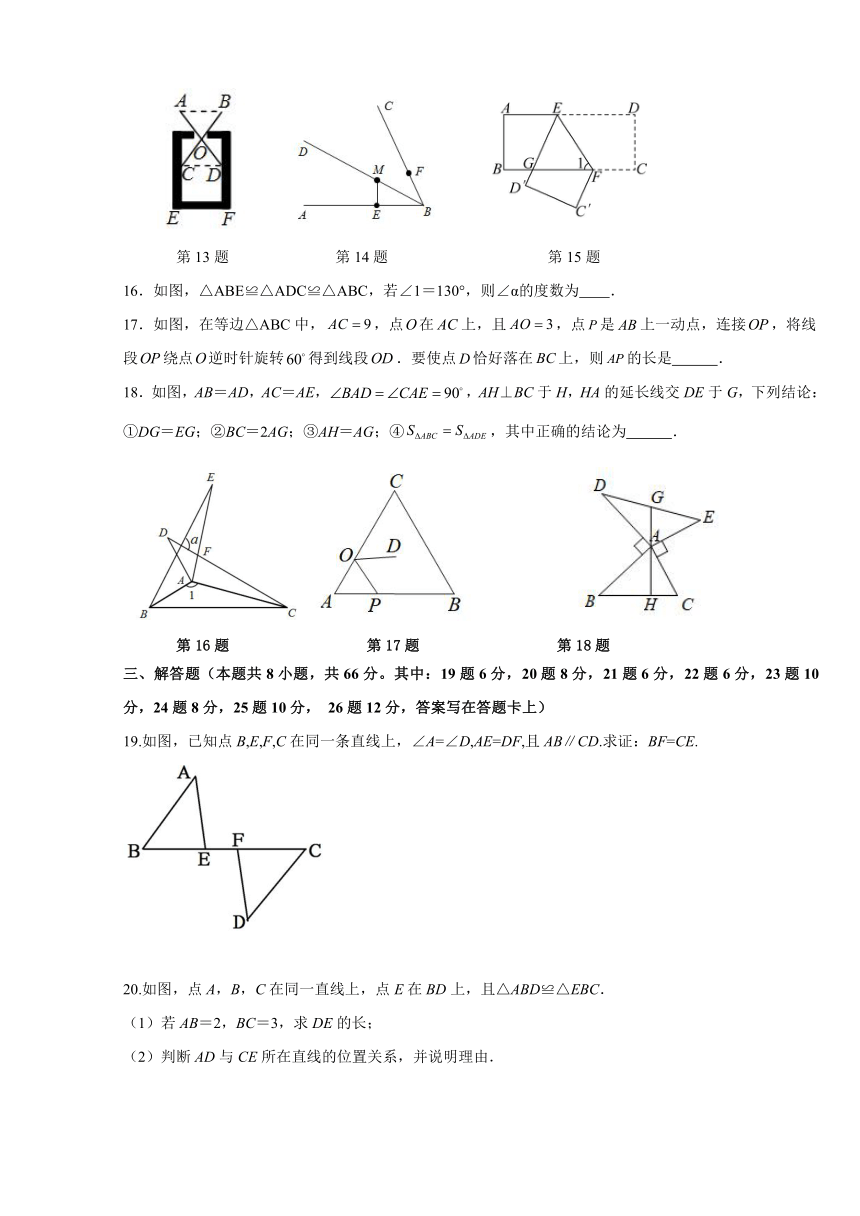
13.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中,,测得,,则圆形容器的壁厚是 cm.
14.如图,BD平分∠ABC,M在BD上,ME⊥AB,F是射线BC上一动点,若ME=4,则MF的最小值为 .
15.如图,把一张长方形的纸条沿折叠,若比多,则 .
第13题 第14题 第15题
16.如图,△ABE≌△ADC≌△ABC,若∠1=130°,则∠α的度数为 .
17.如图,在等边△ABC中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转得到线段.要使点恰好落在上,则的长是 .
18.如图,AB=AD,AC=AE,,AH⊥BC于H,HA的延长线交DE于G,下列结论:①DG=EG;②BC=2AG;③AH=AG;④,其中正确的结论为 .
第16题 第17题 第18题
三、解答题(本题共8小题,共66分。其中:19题6分,20题8分,21题6分,22题6分,23题10分,24题8分,25题10分, 26题12分,答案写在答题卡上)
19.如图,已知点B,E,F,C在同一条直线上,∠A=∠D,AE=DF,且AB∥CD.求证:BF=CE.
20.如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC.
(1)若AB=2,BC=3,求DE的长;
(2)判断AD与CE所在直线的位置关系,并说明理由.
21.尺规作图(保留作图痕迹)
(1)在上找一点P,使点P到和的距离相等;
(2)在射线上找一点Q,使.
22.如图,格点在网格中的位置如图所示
(1)在图中画出△ABC关于直线对称的△A'B'C';
(2)在直线上找一点,使最小.(不写作法,保留作图痕迹)
(3)若网格中每个小正方形的边长为1,则△A'B'C'的面积为 .
23.如图,在中,D是BC的中点,,,垂足分别是E,F,BE=CF.
(1)求证:AD是△ABC的角平分线;
(2)若AB=8,S=36,求DE的长.
24.如图所示,在不等边△ABC中,,,的垂直平分线交边于点,交边于点,垂直平分线交边于点,交边于点.
(1)若,求的度数;
(2)若边长为整数,求的周长.
25.如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系: .
26.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1cm/s和xcm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F
(1)如图1,当x=2时,设点P运动时间为ts,当点P在AC上,点Q在BC上时,
①用含t的式子表示CP和CQ,则CP= cm,CQ= cm;
②当t=2时,△PEC与△QFC全等吗?并说明理由;
(2)请问:当x=3时,△PEC与△QFC有没有可能全等?若能,直接写出符合条件的t值:若不能,请说明理由.
第一次课堂练习试卷
出卷人: 审卷人: 出卷日期: 2023.10
一、单选题(本题共10小题,每小题3分,共30分)
1.下列手机屏幕解锁图形案是轴对称图形的是( )
A. B. C. D.
2.如图,,,,则判定△ABC ≌△ABD 的依据是( )
A. B. C. D.无法确定
3.如图,在△ACD与中,,再添加下列哪个条件,能判定( )
A. B. C.DA平分 D.
4.如图,的面积为垂直于的平分线于点,则的面积为( )
A. B. C. D.
5.如图,在△ABC中,D为线段AB的垂直平分线与BC延长线的交点,连接AD,若AD=7,BC=3,则CD的长为( )
A.3 B.4 C.6 D.7
第2题 第3题 第4题 第5题
如图,在△ABC中,,将△ABC沿着直线l折叠,点C落在点D的位置,则的度数是( )
A. B. C. D.
7.如图,直线AB、CD相交于点O,P为这两条直线外一点,连接OP.点P关于直线AB、CD的对称点分别是点P1、P2.若OP=3.5,则点P1、P2之间的距离可能是( )
A.5 B.9 C.7 D.11
8.如图,在四边形ABCD中,,E为BC的中点,连接DE,AE,,延长DE交AB的延长线于点F.若,则AD的长为( )
A.0 B.6 C.7 D.9
第6题 第7题 第8题
9.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使BPE与CQP全等.
A.1 B.1或4 C.1或2 D.2或4
10.如图,在中,,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①;②;③;④若,则.正确的结论序号是( )
A.①② B.①②④ C.②③④ D.①③④
第9题 第10题
二、填空题(本题共8小题,每小题3分,共24分)
11.已知△ABC△DEF,∠A=50°,∠B=75°,则∠F= .
12.一位球员的球衣号码为,那么他在镜子中看到自己的号码是 .
13.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中,,测得,,则圆形容器的壁厚是 cm.
14.如图,BD平分∠ABC,M在BD上,ME⊥AB,F是射线BC上一动点,若ME=4,则MF的最小值为 .
15.如图,把一张长方形的纸条沿折叠,若比多,则 .
第13题 第14题 第15题
16.如图,△ABE≌△ADC≌△ABC,若∠1=130°,则∠α的度数为 .
17.如图,在等边△ABC中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转得到线段.要使点恰好落在上,则的长是 .
18.如图,AB=AD,AC=AE,,AH⊥BC于H,HA的延长线交DE于G,下列结论:①DG=EG;②BC=2AG;③AH=AG;④,其中正确的结论为 .
第16题 第17题 第18题
三、解答题(本题共8小题,共66分。其中:19题6分,20题8分,21题6分,22题6分,23题10分,24题8分,25题10分, 26题12分,答案写在答题卡上)
19.如图,已知点B,E,F,C在同一条直线上,∠A=∠D,AE=DF,且AB∥CD.求证:BF=CE.
20.如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC.
(1)若AB=2,BC=3,求DE的长;
(2)判断AD与CE所在直线的位置关系,并说明理由.
21.尺规作图(保留作图痕迹)
(1)在上找一点P,使点P到和的距离相等;
(2)在射线上找一点Q,使.
22.如图,格点在网格中的位置如图所示
(1)在图中画出△ABC关于直线对称的△A'B'C';
(2)在直线上找一点,使最小.(不写作法,保留作图痕迹)
(3)若网格中每个小正方形的边长为1,则△A'B'C'的面积为 .
23.如图,在中,D是BC的中点,,,垂足分别是E,F,BE=CF.
(1)求证:AD是△ABC的角平分线;
(2)若AB=8,S=36,求DE的长.
24.如图所示,在不等边△ABC中,,,的垂直平分线交边于点,交边于点,垂直平分线交边于点,交边于点.
(1)若,求的度数;
(2)若边长为整数,求的周长.
25.如图,在△OBC中,边BC的垂直平分线交∠BOC的平分线于点D,连接DB,DC,过点D作DF⊥OC于点F.
(1)若∠BOC=60°,求∠BDC的度数;
(2)若∠BOC=,则∠BDC= ;(直接写出结果)
(3)直接写出OB,OC,OF之间的数量关系: .
26.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1cm/s和xcm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F
(1)如图1,当x=2时,设点P运动时间为ts,当点P在AC上,点Q在BC上时,
①用含t的式子表示CP和CQ,则CP= cm,CQ= cm;
②当t=2时,△PEC与△QFC全等吗?并说明理由;
(2)请问:当x=3时,△PEC与△QFC有没有可能全等?若能,直接写出符合条件的t值:若不能,请说明理由.
同课章节目录
