22.2 相似三角形的判定 第5课时 课件 2023--2024学年沪科版九年级数学上册
文档属性
| 名称 | 22.2 相似三角形的判定 第5课时 课件 2023--2024学年沪科版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1002.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-19 09:49:27 | ||
图片预览



文档简介
(共22张PPT)
22.2 相似三角形的判定
第22章
相似形
第 5 课时 判定两个直角三角形相似
●我们每个人手里都有一把自学成才的钥匙:
理想、勤奋、毅力、虚心和科学方法。
——华罗庚
理解直角三角形相似的特殊判定方法的证明方法.
掌握直角三角形相似的判定. (重点)
能熟练地运用直角三角形相似的判定定理.(难点)
课堂学习总结感悟与知识提升
1
2
3
4
学习目标
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
复习回顾
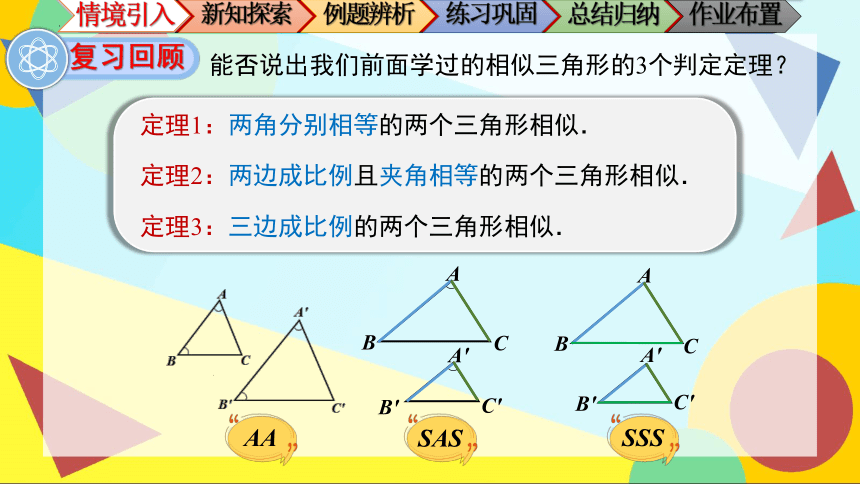
能否说出我们前面学过的相似三角形的3个判定定理?
定理1:两角分别相等的两个三角形相似.
定理2:两边成比例且夹角相等的两个三角形相似.
定理3:三边成比例的两个三角形相似.
A
B
C
A'
C'
B'
A
B
C
A'
C'
B'
AA
SAS
SSS
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
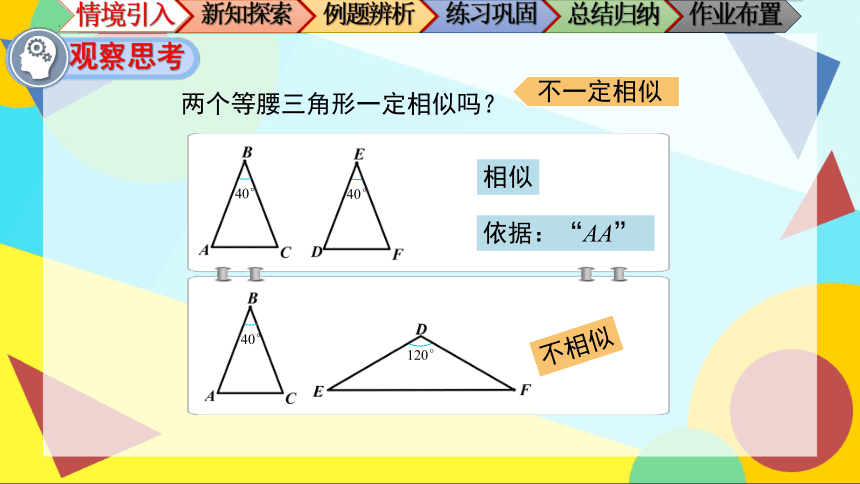
两个等腰三角形一定相似吗?
40°
120°
40°
40°
相似
依据:“AA”
不相似
不一定相似
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
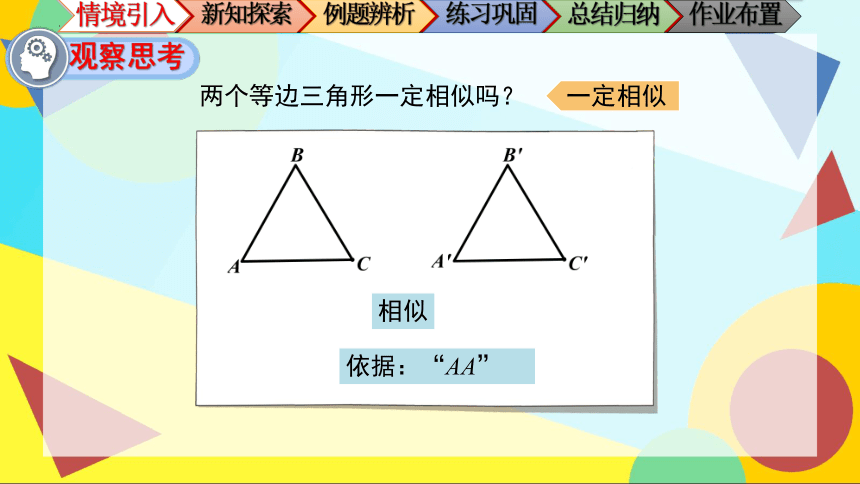
两个等边三角形一定相似吗?
相似
依据:“AA”
一定相似
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
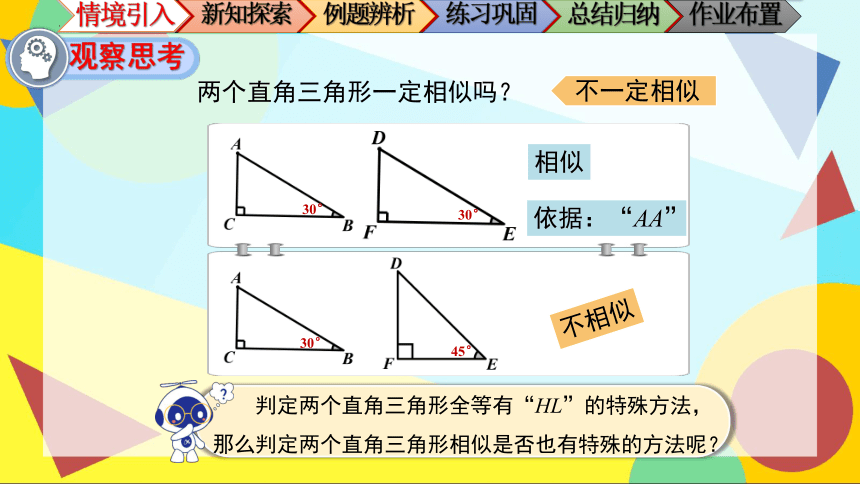
两个直角三角形一定相似吗?
不一定相似
相似
依据:“AA”
不相似
30°
30°
30°
45°
判定两个直角三角形全等有“HL”的特殊方法,那么判定两个直角三角形相似是否也有特殊的方法呢?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
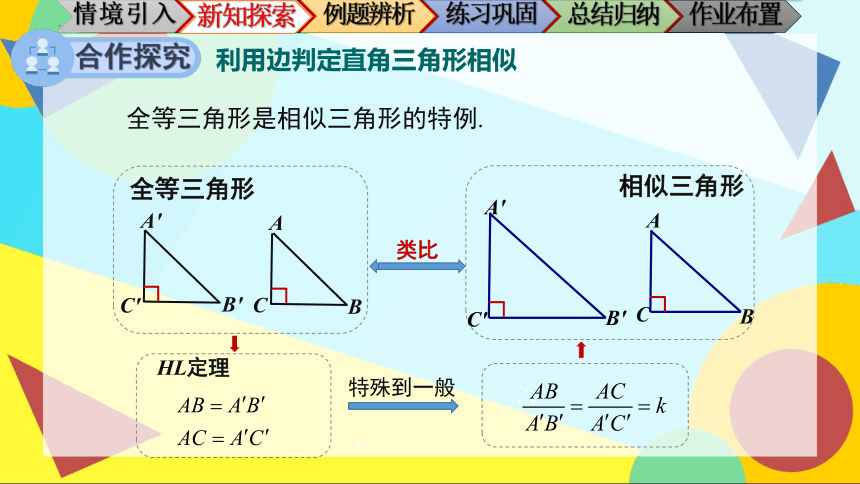
利用边判定直角三角形相似
类比
全等三角形是相似三角形的特例.
HL定理
,
特殊到一般
∴
A'
B'
C'
A
B
C
全等三角形
相似三角形
B'
C'
A'
A
B
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
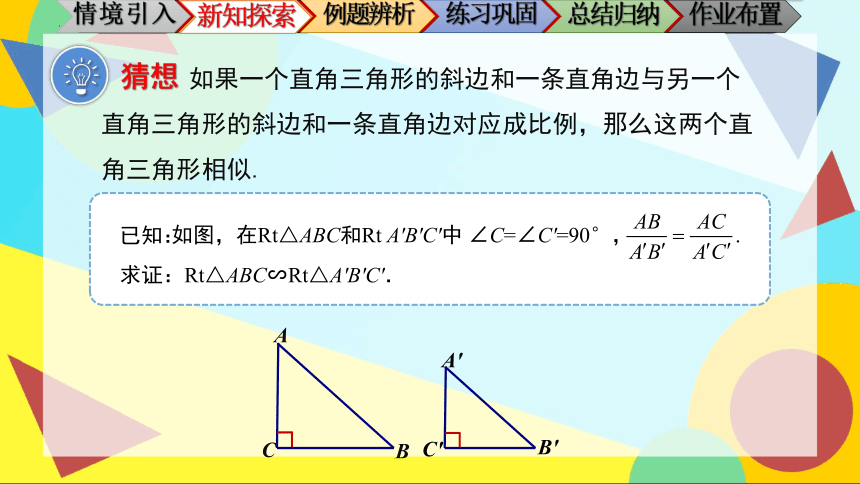
猜想
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
如图,在Rt△ABC和Rt A'B'C'中 ∠C=∠C'=90°, .
求证:Rt△ABC∽Rt△A'B'C'.
已知:
B'
C'
A'
A
B
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
证明
如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°, .
求证:Rt△ABC∽Rt△A'B'C'.
已知:
证明:设
,则AB=kA'B',AC=kA'C'.
∴ .
∴ △ABC∽△A'B'C'.
∵
,
猜想成立
B'
C'
A'
A
B
C
你还有其它的证明方法吗?
设k法
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
归 纳
判定两个直角三角形相似
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
符号语言 :
在RT△ABC 和RT 中,
∴ .
△ABC∽
∵ ∠C=∠C'=90°, ,
B'
C'
A'
A
B
C
注意:判定两个直角三角形相似,除了可用上述特殊的判定方法外,还可用一般三角形相似的判定定理.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
如图,下列四个三角形中,与△ABC相似的是( )
【解析】设网格的边长是1,则
所以AB:AC:BC=1:2:
∴△ABC是直角形三角,且AB∶AC=1∶2,
∵选项A、D选项不是直角三角形,∴排除A、D选项;
∵B选项中的三角形的两直角边的边长比为1∶2,
C选项中的三角形的两直角边的边长比为3∶2,
∴选项B正确.
B
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,∠ABC=∠CDB=90°,CB=a,AC=b.问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似?
A
C
B
D
a
b
分析
(1)题中已知什么?
(2)求证的结论是什么?
△ABC∽△CDB.
在RT△ABC与RT△CDB中, CB=a,AC=b.
不确定对应点,需分类讨论:
△ABC∽△CDB或△ABC∽△BDC
利用“HL”判定方法寻找条件即可
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,∠ABC=∠CDB=90°,CB=a,AC=b.问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似?
A
C
B
D
a
b
解:∵∠ABC=∠CDB=90°,
当 时,△ABC∽△CDB.
即 , .
又当 时,△ABC∽△BDC.
即 , .
答:当 或 时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 3
∴
解:∵ ED⊥AB,∴∠EDA=90 ° .
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
D
A
B
C
E
∴
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件不能判断它们相似的是( )
A. ∠A=∠B′
B. AC=BC,A′C′=B′C′
C. AB=3BC,A′B′=3B′C′
D. △ABC中有两边长为3、4,△A′B′C′中有两边长为6、8
D
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
2.如图:AB=2AC,BD=2AE,且BD⊥AD,AE⊥EC,
求证:△ABD∽△CAE.
∴ △ABD∽△CAE.
证明:∵ BD⊥AD,AE⊥EC,
∴ △ABD和△CAE都是直角三角形.
∴ .
注意:还可以利用“SSS” 判定定理进行证明,你来试试吧!
A
E
C
B
D
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
本节课你有什么收获?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
判定两个直角三角形相似
直角三角形相似的特殊判定方法:
符号语言:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
在RT△ABC 和RT 中,
∴ .
△ABC∽
∵ ∠C=∠C'=90°, ,
B'
C'
A'
A
B
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
两角分别相等
两边对应成比例且夹角相等
三边对应成比
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(AA)
(SAS)
(HL)
(SSS)
检查作业: 习题22.2 第2、3、5题
作 业
读书部分:阅读教材相关章节
书面作业:教材习题22.2 (必做)
22.2.2 (选做)
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
作业布置
同学们,再见!
成功无捷径
学习需奋斗
22.2 相似三角形的判定
第22章
相似形
第 5 课时 判定两个直角三角形相似
●我们每个人手里都有一把自学成才的钥匙:
理想、勤奋、毅力、虚心和科学方法。
——华罗庚
理解直角三角形相似的特殊判定方法的证明方法.
掌握直角三角形相似的判定. (重点)
能熟练地运用直角三角形相似的判定定理.(难点)
课堂学习总结感悟与知识提升
1
2
3
4
学习目标
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
复习回顾
能否说出我们前面学过的相似三角形的3个判定定理?
定理1:两角分别相等的两个三角形相似.
定理2:两边成比例且夹角相等的两个三角形相似.
定理3:三边成比例的两个三角形相似.
A
B
C
A'
C'
B'
A
B
C
A'
C'
B'
AA
SAS
SSS
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
两个等腰三角形一定相似吗?
40°
120°
40°
40°
相似
依据:“AA”
不相似
不一定相似
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
两个等边三角形一定相似吗?
相似
依据:“AA”
一定相似
导入新课
新知探索
例题辨析
练习巩固
总结归纳
作业布置
情境引入
观察思考
两个直角三角形一定相似吗?
不一定相似
相似
依据:“AA”
不相似
30°
30°
30°
45°
判定两个直角三角形全等有“HL”的特殊方法,那么判定两个直角三角形相似是否也有特殊的方法呢?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
合作探究
利用边判定直角三角形相似
类比
全等三角形是相似三角形的特例.
HL定理
,
特殊到一般
∴
A'
B'
C'
A
B
C
全等三角形
相似三角形
B'
C'
A'
A
B
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
猜想
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
如图,在Rt△ABC和Rt A'B'C'中 ∠C=∠C'=90°, .
求证:Rt△ABC∽Rt△A'B'C'.
已知:
B'
C'
A'
A
B
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
证明
如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°, .
求证:Rt△ABC∽Rt△A'B'C'.
已知:
证明:设
,则AB=kA'B',AC=kA'C'.
∴ .
∴ △ABC∽△A'B'C'.
∵
,
猜想成立
B'
C'
A'
A
B
C
你还有其它的证明方法吗?
设k法
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
新知探索
归 纳
判定两个直角三角形相似
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
符号语言 :
在RT△ABC 和RT 中,
∴ .
△ABC∽
∵ ∠C=∠C'=90°, ,
B'
C'
A'
A
B
C
注意:判定两个直角三角形相似,除了可用上述特殊的判定方法外,还可用一般三角形相似的判定定理.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 1
如图,下列四个三角形中,与△ABC相似的是( )
【解析】设网格的边长是1,则
所以AB:AC:BC=1:2:
∴△ABC是直角形三角,且AB∶AC=1∶2,
∵选项A、D选项不是直角三角形,∴排除A、D选项;
∵B选项中的三角形的两直角边的边长比为1∶2,
C选项中的三角形的两直角边的边长比为3∶2,
∴选项B正确.
B
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,∠ABC=∠CDB=90°,CB=a,AC=b.问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似?
A
C
B
D
a
b
分析
(1)题中已知什么?
(2)求证的结论是什么?
△ABC∽△CDB.
在RT△ABC与RT△CDB中, CB=a,AC=b.
不确定对应点,需分类讨论:
△ABC∽△CDB或△ABC∽△BDC
利用“HL”判定方法寻找条件即可
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 2
如图,∠ABC=∠CDB=90°,CB=a,AC=b.问当BD与a,b之间满足怎样的函数表达式时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似?
A
C
B
D
a
b
解:∵∠ABC=∠CDB=90°,
当 时,△ABC∽△CDB.
即 , .
又当 时,△ABC∽△BDC.
即 , .
答:当 或 时,以点A,B,C为顶点的三角形与以点C,D,B为顶点的三角形相似.
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
例题辨析
典例 3
∴
解:∵ ED⊥AB,∴∠EDA=90 ° .
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
D
A
B
C
E
∴
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件不能判断它们相似的是( )
A. ∠A=∠B′
B. AC=BC,A′C′=B′C′
C. AB=3BC,A′B′=3B′C′
D. △ABC中有两边长为3、4,△A′B′C′中有两边长为6、8
D
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
练习巩固
当
堂
练
习
2.如图:AB=2AC,BD=2AE,且BD⊥AD,AE⊥EC,
求证:△ABD∽△CAE.
∴ △ABD∽△CAE.
证明:∵ BD⊥AD,AE⊥EC,
∴ △ABD和△CAE都是直角三角形.
∴ .
注意:还可以利用“SSS” 判定定理进行证明,你来试试吧!
A
E
C
B
D
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
本节课你有什么收获?
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
判定两个直角三角形相似
直角三角形相似的特殊判定方法:
符号语言:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
在RT△ABC 和RT 中,
∴ .
△ABC∽
∵ ∠C=∠C'=90°, ,
B'
C'
A'
A
B
C
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
总结归纳
相似图形三角形的判定方法:
通过定义
平行于三角形一边的直线
两角分别相等
两边对应成比例且夹角相等
三边对应成比
两直角三角形的斜边和一条直角边对应成比例
(三边对应成比例,三角相等)
(AA)
(SAS)
(HL)
(SSS)
检查作业: 习题22.2 第2、3、5题
作 业
读书部分:阅读教材相关章节
书面作业:教材习题22.2 (必做)
22.2.2 (选做)
情境引入
新知探索
例题辨析
练习巩固
总结归纳
作业布置
作业布置
同学们,再见!
成功无捷径
学习需奋斗
